Определение интервала дискретизации

В ряде задач встречается случай, когда необходимо выбрать интервал выборок 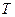аналогового сигнала с учетом требований к сохранению формы сигнала с одной стороны и не слишком сильного «проигрыша» временному интервалу, выбираемому из условий выполнения теоремы Котельникова. Напомним, что основным условием, необходимым для точного выполнения требований теоремы Котельникова является ограниченность ширины спектра обрабатываемого сигнала. В реальных случаях сигналы имеют конечную длительность, а, следовательно, ширина спектра не ограничена.

Очевидно, что в этом случае представление непрерывного сигнала последовательностью отсчетов будет сопровождаться ошибкой. Величина этой ошибки будет определяться той частью спектра, которая соответствует частотам выше некоторой граничной частоты, выбираемой из тех или иных соображений. Уменьшение ошибки достигается уменьшением временного интервала между соседними выборочными значениями сигнала.

Такие задачи встречаются при преобразовании цифровых звуковых сигналов, записанных на компакт-дисках, в аналоговую форму с заранее заданным уровнем искажений. Очевидно, что уменьшение временного интервала между выборками приводит к удорожанию аппаратуры, что является нежелательным.

Поэтому следует выбирать временной интервал 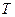хотя и меньшим, но максимально близким по величине к величине временного интервала, определяемого из условий выполнения теоремы Котельникова для той или иной задачи.

Для определения величины временного интервала 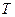используется представление, что ФНЧ, применяемый для «сглаживания» выборочных отсчетов, является «идеальным» и имеет частоту среза 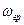. Видно, что подобная задача является «обратной» относительно задачи, рассмотренной выше в п.4.1.

Пример 13. Интервал дискретизации выбирается из условия 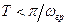, где 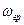– граничная частота для сигнала с ограниченным спектром. Выбрать интервал дискретизации прямоугольного импульса длительностью 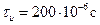и определить необходимое число отсчетов 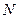. В качестве наивысшей частоты взять ту точку на частотной оси, когда спектральная плотность обращается в нуль и за которой величина спектральной плотности не превышает 0,1 от максимального нормированного значения (т.е. менее 0,1).

Исходя из ранее сделанных замечаний, видно, что точка на частотной оси, когда спектральная плотность обращается в нуль и за которой величина спектральной плотности не превысит 0,1 от максимального нормированного значения, располагается между вторым и третьим БЛ, а, следовательно, будет равна величине

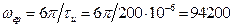(рад/с),

или

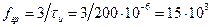(Гц).

Тогда величина 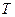, определяющая временной интервал между выборками будет

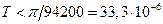(с).

Количество отсчетов 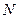будет

.

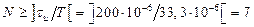Аналогичным образом решаются все задачи в п.10.2.5. в [2].

Дата добавления: 2014-12-24