Согласованная фильтрация

Как известно, максимальное отношение сигнал/шум 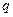достигается на выходе того или иного фильтра, называемого согласованным для заданного входного сигнала 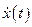, при выполнении условия, а именно:

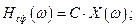(4.2)

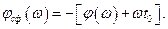
Здесь обозначено 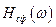– АЧХ согласованного фильтра (СФ); 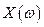– амплитудно-частотный спектр (АЧС) входного сигнала 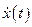; 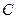– коэффициент пропорциональности; 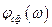– фазочастотная характеристика СФ; 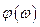– фазочастотный спектр входного сигнала 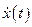; 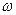– несущая частота входного сигнала (рад/с); – момент времени окончания входного сигнала на входе СФ и численно равный длительности входного сигнала 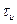(с).

Видно, что АЧХ СФ является комплексно-сопряженной функцией относительно функции, описывающей амплитудно-фазочастотный спектр обрабатываемого входного сигнала .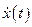

Во временной области работа СФ описывается интегралом свертки (2.1) в виде

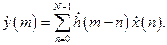
При этом вид ИХ СФ описывается выражением

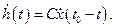........... (4.3)

Количество отсчетов выходного сигнала равно величине 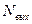, связанной с количеством отсчетов входного сигнала 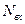и количеством отсчетов ИХ СФ 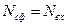выражением

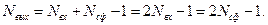(4.4)

Известно, что преобразование Фурье интеграла свертки имеет вид

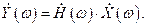
Для СФ, учитывая вышеизложенное и выражение (4.2), огибающую амплитудно-фазочастотного спектра, т.е. амплитудно-частотный спектр (АЧС), можно записать в виде

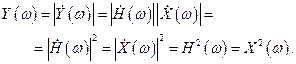(4.5)

Для входного прямоугольного импульса 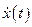длительности 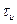форма АЧС 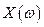, как указывалось выше, описывается функцией вида .

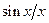Тогда из выражения (4.5) видно, что форма АЧС выходного сигнала будет описываться функцией в виде

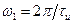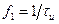Тогда очевидно, что для видеоимпульса прямоугольной формы максимум первого БЛ располагается на частотной оси между точкой или и точко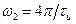й или 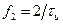в точке 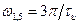или 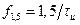. Амплитуда первого БЛ будет равна 0,045 от максимального значения, равного единице.

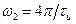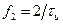Максимум второго БЛ будет располагаться на частотной оси между точкой или и точко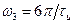й или 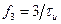в точке 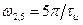или 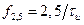. Амплитуда второго БЛ будет равна 0,0162 от максимального значения, равного единице.

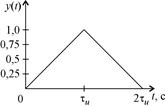
Как видно из (4.3), форма ИХ СФ для входного сигнала прямоугольной формы также будет иметь прямоугольную форму. Следовательно, отклик СФ на входной импульс с прямоугольной огибающей примет вид треугольного импульса с количеством отсчетов, определяемых выражением (4.4).

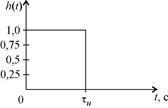
На рис. 20,а изображена огибающая прямоугольного видеоимпульса, на рис. 20,б изображена огибающая ИХ СФ для прямоугольного видеоимпульса, а на рис. 20,в изображена треугольная огибающая отклика СФ на воздействие входного видеоимпульса прямоугольной формы.

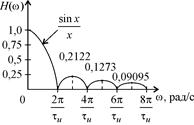
На рис. 21,а изображен АЧС входного видеоимпульса прямоугольной формы, на рис. 21,б изображена АЧХ СФ для обработки видеоимпульса прямоугольной формы, а на рис. 21,в изображен АЧС выходного сигнала треугольной формы.

а)	а)
б)	б)
в)	в)
Рис. 20. Формы входного сигнала, ИХ СФ и выходного сигнала	Рис 21. Формы АЧС входного сигнала, АЧХ СФ и АЧС выходного сигнала

Пример 14. Импульс прямоугольной формы длительностью 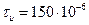(с) проходит СФ. Определить интервал дискретизации 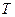и число отсчетов 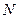для импульса на выходе СФ, полагая 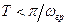, и при условии, что наивысшая 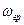является та точка на частотной оси, когда спектральная плотность равна нулю и после которой величина нормированной спектральной плотности меньше 0,04. Привести огибающую ИХ СФ, огибающую его АЧХ, виды сигналов на входе и выходе СФ и их спектры.

Определим, предварительно, величину 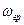(рад/с).

Из сделанных выше замечаний следует, что величина

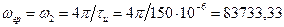(рад/с),

поскольку нулевая точка для заданных условий расположена между первым и вторым БЛ выходного АЧС обработанного в СФ сигнала.

Интервал дискретизации будет

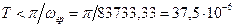(с).

Определим, предварительно, величину

.

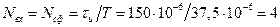Тогда, учитывая выражение (4.4) найдем величину

.

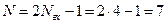Форма входного сигнала, форма ИХ СФ и форма выходного сигнала такие же, как и изображенные на рис. 20, а форма АЧС входного сигнала, АЧХ СФ и АЧС выходного сигнала изображены на рис. 21.

Очевидно, что для каждой конкретной задачи необходимо будет на соответствующих рисунках (в контрольных работах или при выполнении домашнего задания) подставить соответствующие цифровые данные, соответствующие заданному варианту.

Аналогичным образом решаются все задачи в п.10.2.6. в [2].

Дата добавления: 2014-12-24