Дискретное преобразование Фурье

Вычисление отсчетов дискретного преобразования Фурье осуществляется в соответствии с выражением

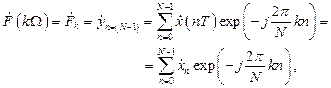(2.8)

где (рад) – бин, т.е. минимальный фазовый сдвиг от отсчета к отсчету за интервал времени, равный периоду дискретизации 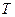, который полагается равным единице; 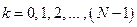– номера частотных составляющих, количество которых равно величине 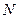; 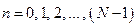– номера отсчетов обрабатываемого сигнала во времени; 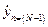– выходной отклик в момент времени , величина которого равна значению коэффициента Фурье.

Раскрывая выражение (2.8), получим формулы для расчета каждого коэффициента Фурье, которые примут вид

(2.9)

В том случае, если

где (рад) – начальная фаза, то видно, что сигнал представляет собой отсчеты комплексной синусоиды, амплитуда которой равна единице, т.е. огибающая сигнала имеет прямоугольную форму. Известно, что сигнал с прямоугольной огибающей имеет форму спектра в виде 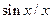. При этом расположение спектра на частотной оси, форма которого 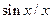, определяется частотой заполнения сигнала.

Пример 5. Вычислить дискретное преобразование Фурье сигнала

согласно выражения (2.8) для значений и . Величина 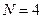. Изобразить на рисунке полученный спектр (в виде сплошных линий) и его огибающую (пунктиром).

Для упрощения расчетов сделаем ряд преобразований. Учтем, что на форму огибающей спектра не оказывает влияние величина начальной фазы. В рассматриваемом случае 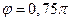(рад). Тогда сигнал может быть переписан в виде

.

Очевидно, что результат не изменится, если вместо сигнала 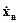рассматривать сигнал

.

Также учтем, что Воспользуемся выражениями (2.9) и определим величину бина для данной задачи, которая будет 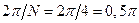(рад).

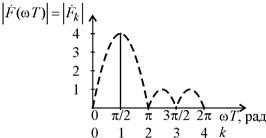
На рис. 3 изображен полученный амплитудный спектр в виде сплошных линий, что соответствует отклику соответствующих частотно-избирательных цепей, вычисляющих дискретное преобразование Фурье, а пунктирными линиями – его огибающая.

Рис. 3. Рассчитанный спектр сигнала и его огибающая

Видно, что центральная частота сигнала расположена на частоте, которая составляет одну четвертую часть частоты дискретизации.

Аналогичным образом решаются все задачи в п.10.1.5. в [2].

2.3. Связь Z -преобразования с преобразованием Лапласа

Известно, что изображение по Лапласу временных процессов, а также передаточных функций линейных цепей отображается в виде точек в р- плоскости в ее левой части. При дискретизации происходит «размножение» этих точек с периодом . Это может быть отображено на р -плоскости в виде бесконечного множества, повторяющихся с периодом , точек.

Для сохранения прежнего количества точек для описания дискретной функции, которую получают путем дискретизации аналоговой временной функции, описываемой точками, вводят новую переменную , расположенную в Z -плоскости.

Переменная 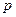в р -плоскости связана с переменной в Z-плоскости соотношением [1]

,

где ; 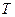– период дискретизации (с).

Из рассмотрения величины 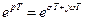видно, что она состоит из модуля, равного величине 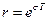и показывающего, как изменяется амплитуда функции от отсчета к отсчету, и величины , показывающей, как изменяется фазовый угол этой амплитуды от отсчета к отсчету.

Очевидно, необходимо чтобы амплитуда сигнала уменьшалась от отсчета к отсчету. Это соответствует тому, что амплитуда процесса во времени постепенно «затухает», как происходит во всех реальных линейных системах, либо амплитуда не изменялась бы, что соответствует процессу на выходе «идеального» генератора.

Для этого необходимо, чтобы величина .

Если величина , то в этом случае амплитуда процесса будет нарастать от отсчета к отсчету, что противоречит работе реальных пассивных линейных систем.

При 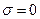, т.е. тогда, когда величина 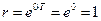, переменная 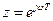. Величина обратная переменной определяется в виде 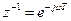и описывает цифровой элемент задержки, осуществляющий задержку отсчета на период дискретизации .

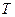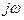Таким образом, каждая точка на р -плоскости описывается в декартовой системе координат. При этом по оси абсцисс, обозначаемой действительной величиной , откладывается величина , а по оси ординат, обозначаемой мнимой величиной , откладывается величина (рад/с).

На Z -плоскости соответствующая точка описывается в полярной системе координат. При этом фазовый угол (рад) откладывается от оси абсцисс. Расстояние от точки, из которой начинается ось абсцисс, до местонахождения искомой точки по радиусу под углом (рад), будет равно величине .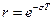

Пример 6. По заданным параметрам, полагая 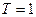(с), вычислить значения и нарисовать на рисунке взаимно-однозначное положение точек на р- и Z -плоскостях. Объяснить, почему значение задано отрицательной величиной.

Пусть , а , т.е. .

Эти две величины определяют положение соответствующей точки на р -плоскости в декартовой системе координат в соответствии с выражениями:

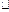по оси абсцисс, обозначаемой , величина ;

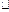по оси ординат, обозначаемой 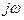, величина (рад/с).

Положение точки на Z -плоскости в полярной системе координат определится в соответствии с выражениями:

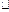угол равен 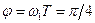(рад);

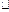величина радиуса .

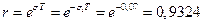На рис. 4 изображено положение рассмотренной точки 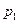на р -плоскости, а на рис. 5 – показан ее переход в положение 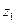на Z -плоскости.

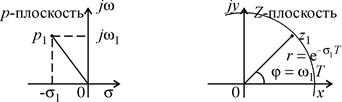
Рис. 4. Положение точки на р -плоскости	Рис. 5. Положение точки на Z -плоскости

Поскольку положение точек на р -плоскости периодически повторяется, то, следовательно, на Z -плоскости эти точки накладываются друг на друга.

Аналогичным образом решаются все задачи в п.10.1.6. в [2].

Дата добавления: 2014-12-24