Вычисление скоростей точек тела, совершающего плоскопараллельное движение

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5

Пример 2.3

Стрелка гальванометра длиной 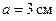колеблется вокруг неподвижной оси по закону Определить ускорение конца стрелки в ее среднем и крайних положениях, если период колебаний , а угловая амплитуда

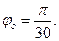
Прежде всего, зная закон вращения, определим угловую скорость и угловое ускорение тела:

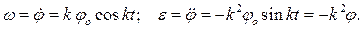
Используя формулы (2.3), определяем касательное и нормальное ускорения точки:

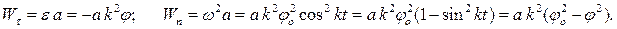
Период связан с круговой частотой соотношением 2 .

Для среднего положения стрелки имеем:

Для крайних положений стрелки имеем:

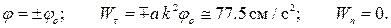
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 13.6; 13.14; 13.17; 13.18; 14.4; 14.5; 14.10.

В любой момент времени скорости любых двух точек плоской фигуры 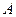и 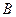связаны равенством

Рис. 2.3

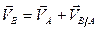(a)

Вектор представляет собой скорость, полученную точкой 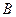при вращении плоской фигуры вокруг оси, проходящей через полюс 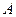перпендикулярно плоской фигуре. Этот вектор направлен перпендикулярно отрезку 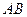(по касательной к окружности, которую описывает точка 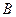при вращении тела вокруг оси 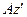), причем в сторону вращения тела (Рис. 2.3). В соответствии с формулой Эйлера

Дата добавления: 2014-12-25