Пример 2.8

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6

Определить скорость и ускорение ползуна 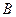кривошипного механизма, а также угловую скорость и угловое ускорение шатуна 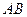в положении, изображенном на Рис. 2.9. Кривошип 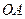вращается замедленно, имея в данный момент времени угловую скорость 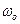и угловое ускорение 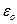. Ползун движется по криволинейной направляющей, имеющей в данном положении механизма радиус кривизны 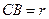. Дано: .

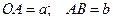Зная направления скоростей точек 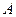и 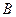, построим мгновенный центр скоростей 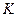стержня 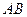, после чего определим угловую скорость стержня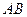

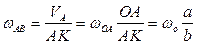
и скорость точки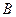

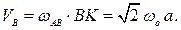
Попытка определить угловое ускорение стержня 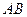, используя определение

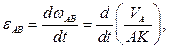
закончится неудачей, поскольку зависимость 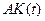неизвестна.

Для определения ускорения точки 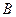принимаем за полюс точку 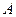. Поскольку известны траектории всех точек во всех их движениях, представим ускорения точек их составляющими:

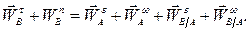
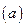
Вычислим векторы, входящие в уравнение .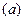

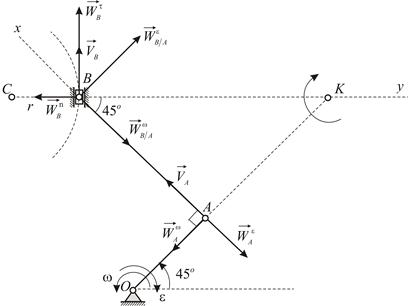
Рис. 2.9

Точка 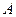принадлежит вращающемуся телу 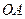. Определяем модули составляющих ускорения этой точки:

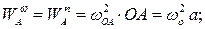
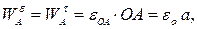
направления векторов показаны на Рис. 2.9.

Точка 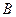движется по криволинейной направляющей. Касательное и нормальное ускорения точки 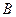определяются по формулам:

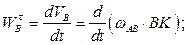
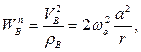
направления составляющих ускорения показаны на Рис. 2.9. По приведенной формуле не удается вычислить касательное ускорение точки 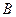, поскольку неизвестны зависимости расстояни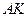й и 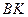от времени.

Находим составляющие ускорения, полученного точкой 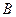при вращении шатуна 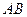вокруг оси 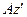. Заметим, что вращательное ускорение остается неизвестным по модулю, поскольку неизвестно угловое ускорение шатуна:

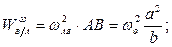
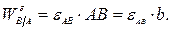
Таким образом, из шести векторов, входящих в равенство 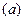, только два неизвестны по модулю. Определим эти неизвестные из уравнения 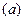. Это уравнение можно решить аналитически или геометрически. Рассмотрим оба способа решения.

Имеет смысл выбрать координатные оси так, чтобы в каждое уравнение в проекциях входила только одна неизвестная. Направим ос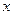ь вдоль 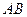(перпендикулярно 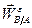), а ось 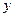по направлению 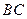(перпендикулярно 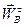). Записывая уравнение 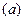в проекциях на ось 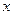, получаем:

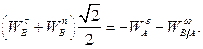
Отсюда

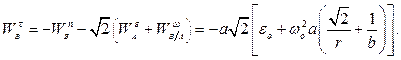
Отрицательный знак говорит о том, что предполагаемое направление вектора 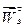было выбрано ошибочно; в действительности этот вектор направлен в противоположную сторону.

Записывая уравнение 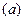в проекциях на ось 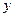, получаем:

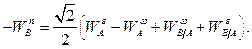
Отсюда

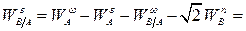
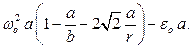
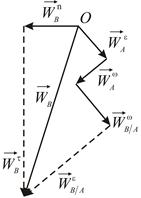
Рис. 2.10

Вычислив 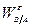, можем определить угловое ускорение стержня :

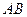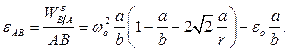
Рассмотрим геометрический способ решения уравнения 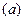. Построим в масштабе сумму векторов, стоящих в правой части уравнения 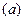. От некоторой точки 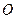отложим 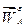, от его конца отложим 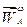, а затем 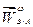(Рис. 2.10). Остается построить 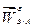, модуль которого неизвестен. Проведем через конец 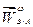пунктирную прямую, параллельную 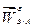. Конец суммы векторов, стоящих в правой части уравнения 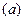, лежит на этой прямой.

Обратимся к левой части уравнения 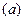. Отложим от точки 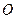известный вектор 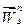. Через его конец проведем пунктирную прямую, параллельную вектору 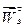. Точка пересечения построенных прямых определяет положение конца вектора ускорения точки .

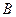Дата добавления: 2014-12-25