
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение параметров нелинейной модели диода
|
|
|
|
Упрощенная статическая (для режима постоянного тока) нелинейная модель полупроводникового диода приведена на рис. 3.
| Рис. 3. Упрощенная статическая нелинейная модель полупровод-никового диода (направления токов показаны для прямого включения) | 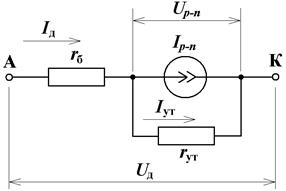
|
Параметрами модели являются объемное сопротивление полупроводниковых областей диода (так называемое сопротивление базы r б), сопротивление утечки p-n- перехода r ут (данный параметр аналогичен описанному выше параметру r ут для кусочно-линейной модели диода) и ток p-n- перехода Ip-n, зависящий от напряжения на этом переходе Up-n. Данная зависимость описывается нелинейным уравнением
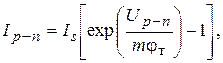 (2)
(2)
где Is – тепловой ток насыщения p-n- перехода, неизменный для данной температуры; m – коэффициент, определяемый свойствами конкретного p-n- перехода (его значения изменяются от 1 до нескольких единиц); φт – тепловой (температурный) потенциал. Зависимость φт от температуры описывается выражением

где k = 1,38·10-23 Дж/К – постоянная Больцмана; T – абсолютная температура, К; е = 1,6·10-19 Кл – заряд электрона.
При нормальной температуре (T = 300 К) φт ≈ 0,026 В.
Таким образом, нашей задачей является определение неизвестных пока параметров нелинейной модели диода r б, r ут, Is и m.
Сопротивление утечки r ут определяется так же, как и для кусочно-линейной модели диода.
Параметры r б и m определяются по прямой ветви ВАХ с помощью так называемого метода выравнивания характеристик. Суть метода заключается в том, что нелинейная зависимость I = f (U), описываемая нелинейным уравнением, заменяется эквивалентной линейной зависимостью в новой системе координат (назовем их условно x и y). Эта эквивалентная зависимость описывается классическим уравнением прямой y = b + kx с легко определяемыми параметрами b и k. Найдя эти параметры, можно перейти к исходному нелинейному уравнению и определить его коэффициенты.
Проиллюстрируем данный метод на примере – найдем параметры нелинейной модели диода (рис. 3), прямая ветвь ВАХ которого представлена на рис. 4.

| Рис. 4. К определению параметров нелинейной модели диода по прямой ветви его вольт-амперной характеристики |
Уравнение (2) можно переписать в виде
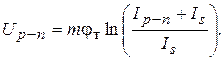 (3)
(3)
С учетом выражения (3) внешнее напряжение на диоде U д можно связать с его током I д следующим соотношением:
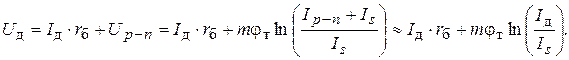 (4)
(4)
Показанное в выражении (4) упрощение возможно лишь в случае включения диода в прямом направлении, когда тепловым током насыщения Is и током утечки I ут можно пренебречь по сравнению с током p-n- перехода Ip-n (он превышает их на несколько порядков величины). Поэтому и можно считать, что I д = Ip-n + I ут ≈ Ip-n, а Ip-n + Is ≈ Ip-n ≈ I д.
Найти параметры r б и m можно, вспомнив, как определяется понятие дифференциального сопротивления – 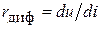 . Если имеется графическая зависимость I = f (U) (ВАХ), дифференциальное сопротивление можно определить по наклону касательной, проведенной к этой ВАХ в какой-либо ее точке. Очевидно, что при нелинейном характере зависимости I = f (U), характерном для диода, значение r диф будет различно для различных точек этой зависимости.
. Если имеется графическая зависимость I = f (U) (ВАХ), дифференциальное сопротивление можно определить по наклону касательной, проведенной к этой ВАХ в какой-либо ее точке. Очевидно, что при нелинейном характере зависимости I = f (U), характерном для диода, значение r диф будет различно для различных точек этой зависимости.
Найдем выражение для дифференциального сопротивления диода, взяв производную от правой части выражения (4) по току I д:
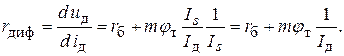 (5)
(5)
Если представить, что r диф – это зависимая переменная, а величина  – независимая переменная, то графиком функции
– независимая переменная, то графиком функции 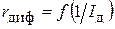 будет прямая. Действительно, уравнение (5) является по сути уравнением прямой вида y = b + kx, где y = r диф,
будет прямая. Действительно, уравнение (5) является по сути уравнением прямой вида y = b + kx, где y = r диф,  , а величины r б и m φт – коэффициенты b и k соответственно. Именно эти коэффициенты мы и будем искать.
, а величины r б и m φт – коэффициенты b и k соответственно. Именно эти коэффициенты мы и будем искать.
Так как графиком функции y = b + kx является прямая, для его построения достаточно найти две принадлежащие этой прямой точки. Отметим на прямой ветви вольт-амперной характеристики диода две произвольные точки 1 и 2 (рис. 4). Для большей точности определения параметров r б и m φт точки следует выбирать на участках ВАХ, имеющих значительно отличающуюся крутизну. Проведем через эти точки две касательные к характеристике. Значения дифференциальных сопротивлений определяются как котангенсы углов наклона этих касательных (при этом необходимо учитывать различие масштабов по осям тока и напряжения), но можно поступить и так, как мы определяли r пр в кусочно-линейной модели диода. Величину r диф можно найти как отношение длин катетов прямоугольного треугольника, гипотенузой которого является проведенная касательная (рис. 4):
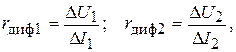
где r диф1, r диф2 – значения дифференциального сопротивления диода в точках 1 и 2 соответственно.
Для показанной на рис. 4 характеристики
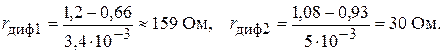
Величины  для выбранных точек 1 и 2 составляют
для выбранных точек 1 и 2 составляют
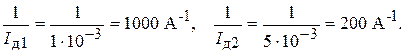
Построим зависимость (5) в системе координат 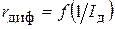 . Для этого отметим две точки (назовем их условно 1 ’ и 2 ’) с найденными только что координатами
. Для этого отметим две точки (назовем их условно 1 ’ и 2 ’) с найденными только что координатами  ,
,  и соединим их прямой (рис. 5). Точка пересечения этой прямой с осью r диф определяет значение r б. Действительно, когда второе слагаемое в выражении (5) обращается в ноль, т.е. когда
и соединим их прямой (рис. 5). Точка пересечения этой прямой с осью r диф определяет значение r б. Действительно, когда второе слагаемое в выражении (5) обращается в ноль, т.е. когда  = 0 и мы находимся на оси r диф, r диф = r б. Для показанной на рис. 5 зависимости r б ≈ 2 Ом.
= 0 и мы находимся на оси r диф, r диф = r б. Для показанной на рис. 5 зависимости r б ≈ 2 Ом.

| Рис. 5. Зависимость r диф = f (1/ I д), соответствующая вольт-амперной характеристике диода, приведенной на рис. 4 |
Значение произведения m φт в соответствии с выражением (5), являющимся для системы координат 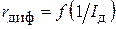 уравнением прямой, найдем по отношению разности координат двух точек на этой прямой. Удобнее использовать уже известные нам координаты точек 1 ’ и 2 ’. Тогда
уравнением прямой, найдем по отношению разности координат двух точек на этой прямой. Удобнее использовать уже известные нам координаты точек 1 ’ и 2 ’. Тогда

Зная величину φт для данной температуры, можно отдельно найти значение коэффициента m. Например, в нашем случае при T = 293 К, когда φт ≈ 0,025 В, m = 0,16/0,025 = 6,4.
Значение теплового тока насыщения p-n- перехода Is найдем, преобразовав выражение (2) и подставив в него координаты произвольной точки на ВАХ диода (например, точки 2) и найденные параметры r б и m φт. При этом, исходя из нелинейной модели диода (рис. 3), в качестве напряжения на p-n- переходе Up-n мы будем подставлять разность внешнего напряжения на диоде U д и падения напряжения на сопротивлении r б:

Методические указания к решению задач 11–20
По справочным вольт-амперным характеристикам биполярного транзистора (рис. 6) определим параметры его малосигнальных моделей в h- и y- параметрах в усилительной области при токе базы I б = 400 мкА и напряжении U кэ = 6 В.
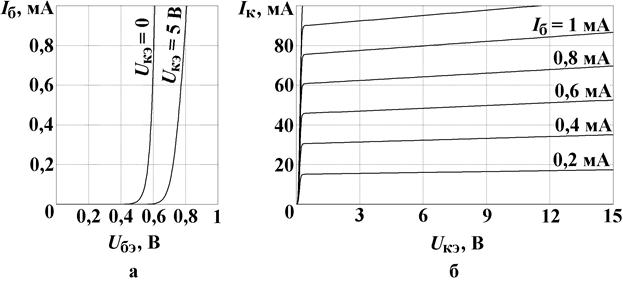 Рис. 6. Семейства входных (а) и выходных (б) ВАХ биполярного транзистора
Рис. 6. Семейства входных (а) и выходных (б) ВАХ биполярного транзистора
При анализе работы усилителя на биполярном транзисторе по переменному току (малосигнальный анализ) транзистор заменяют его малосигнальной моделью, представляющей собой классический четырехполюсник. Наиболее распространены малосигнальные модели в так называемых h- (рис. 7, а) и y- параметрах (рис. 7, б). При этом h- параметры легче определить, зато y- параметры удобнее использовать.

Рис. 7. Малосигнальные модели биполярного транзистора: а – модель в h- параметрах; б – модель в y- параметрах
При малосигнальном анализе рассматривается работа транзистора в режиме усиления переменного входного сигнала малой амплитуды, когда абсолютные значения входного тока и входного напряжения транзистора мало изменяются по сравнению с их постоянными составляющими (рис. 8). В этом случае транзистор можно описать системой линейных уравнений.

| Рис. 8. Временнáя диаграмма напряжения в режиме малого сигнала: U = – постоянная составляющая напряжения; u ~ – переменная составляющая |
Для модели в h- параметрах независимыми величинами являются переменные составляющие входного тока i вх и выходного напряжения u вых, а зависящими от них величинами – переменные составляющие выходного тока i вых и входного напряжения u вх:
 (6)
(6)
При включении биполярного транзистора по схеме с общим эмиттером систему (6) следует записать в виде
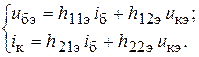 (7)
(7)
Буква «Э» в индексах h- параметров обозначает схему включения транзистора (при включении транзистора по схеме с общей базой или общим коллектором в обозначениях h- параметров появятся буквы «Б» и «К» соответственно; входными токами и напряжениями, выходными токами и напряжениями будут i э, u бэ, i к, u кб и i б, u бэ, i э, u кэ соответственно).
Значения h- параметров можно определить по входным и выходным ВАХ транзистора в окрестностях предварительно найденной точки покоя. Исходя из уравнений (7) параметр h 11э должен определяться как
 (8)
(8)
где Δ U бэ, Δ I б – малые изменения абсолютных значений напряжения и тока базы транзистора вблизи точки покоя; U кэ.п – выходное (в данном случае коллекторное) напряжение транзистора в точке покоя.
Поскольку параметр h 11 определяется как отношение входных напряжения и тока, он должен называться входным сопротивлением транзистора.
Аналогично определяются остальные h- параметры биполярного транзистора:
 (9)
(9)
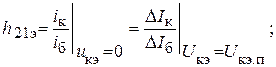 (10)
(10)
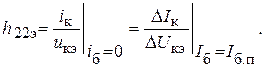 (11)
(11)
Здесь I б.п – входной ток транзистора (ток базы) в точке покоя; Δ U кэ, Δ I к – малые изменения абсолютных значений коллекторных напряжения и тока вблизи точки покоя.
Параметры h 12, h 21, h 22 называются соответственно коэффициентом обратной связи по напряжению, коэффициентом передачи входного тока и выходной проводимостью транзистора.
Параметры h 11 и h 12 определяются по входным ВАХ биполярного транзистора, а h 21 и h 22 – по выходным ВАХ. При этом коэффициент обратной связи по напряжению h 12 обычно настолько мал, что на практике можно считать его равным нулю.
Пусть в режиме покоя биполярный транзистор характеризуется следующими значениями тока и напряжения: I б.п = 600 мкА, U кэ.п = 6 В. Определим по входным ВАХ входное сопротивление транзистора h 11э в окрестностях точки покоя (рис. 9). Для выполнения условия U кэ = U кэ.п в выражении (8) мы должны использовать ветвь ВАХ, соответствующую выходному напряжению U кэ = 6 В, которая отсутствует на приведенной характеристике. В то же время известно, что при работе биполярного транзистора в усилительном режиме ветви его входных ВАХ, соответствующие различным значениям выходного напряжения, с увеличением этого напряжения свыше 2–3 В проходят настолько близко друг к другу, что практически сливаются в одну. Поэтому на рис. 9 мы отметили точку покоя А на имеющейся в нашем распоряжении ветви характеристики, соответствующей U кэ = 5 В.

| Рис. 9. К определению параметра h 11э по входной вольт-амперной характеристике транзистора |
Отметим на этой же ветви ВАХ рядом с точкой А две дополнительные точки B и C (чуть выше и чуть ниже точки покоя, как это показано на рис. 9). Тогда в соответствии с выражением (8) входное сопротивление транзистора в окрестностях точки покоя будет определяться как отношение разностей координат точек B и C:
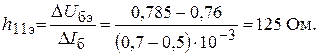
Параметры h 21 и h 22 определим по выходным ВАХ транзистора (рис. 10). Точкой покоя транзистора на выходных ВАХ является D.
Условием определения коэффициента передачи входного тока h 21э согласно выражению (10) является неизменность выходного напряжения U кэ = U кэ.п = 6 В. Выполняя данное условие, отметим на выходных ВАХ (рис. 10, а) две дополнительные точки E и F – точки пересечения прямой, описываемой уравнением U кэ = 6 В (вертикальная пунктирная прямая), с ветвями ВАХ, лежащими чуть выше и чуть ниже ветви, соответствующей току базы покоя I б.п = 0,6 мА. В данном случае мы выбрали ближайшие ветви ВАХ, соответствующие значениям тока базы 0,8 и 0,4 мА. Согласно выражению (10)

В качестве Δ I б мы подставили разность значений тока базы для точек E и F.

Рис. 10. К определению параметров h 21э (а) и h 22э (б) по выходным вольт-амперным характеристикам биполярного транзистора
Условием определения выходной проводимости h 22э согласно выражению (11) является неизменность входного тока I б = I б.п = 0,6 мА, т.е. мы должны оставаться на ветви ВАХ, соответствующей этому току. Выполняя данное условие, отметим на ней две дополнительные точки L и M слева и справа от точки покоя D (рис. 10, б). Строго говоря, мы должны отметить эти точки как можно ближе к точке покоя, исходя из самого понятия малосигнальной модели. Но как видно из рис. 10, б, ветвь ВАХ почти на всем своем протяжении является прямолинейной, и мы можем расставить точки L и M на большее расстояние – в этом случае нам будем удобнее измерять разность их координат по вертикальной оси (оси тока). Выходная проводимость h 22э находится как отношение разностей координат точек M и N:

Простые, как было только что показано, в определении, h- параметры, тем не менее, не очень удобно применять при малосигнальном анализе. Все дело в их «разнородности» – среди них есть и безразмерные коэффициенты (h 12, h 21), и сопротивление (h 11), и проводимость (h 22). Поэтому при составлении системы уравнений для транзисторной схемы по методу узловых потенциалов, когда потенциалы узлов схемы связывают друг с другом посредством проводимостей ветвей, удобнее использовать малосигнальную модель биполярного транзистора в y- параметрах (рис. 7, б). Эта модель описывается системой уравнений
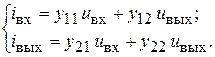 (12)
(12)
При включении транзистора по схеме с общим эмиттером система (12) преобразуется к виду
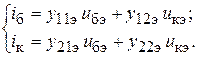 (13)
(13)
Очевидно, что y- параметры, связывающие переменные составляющие напряжений (независимые величины) с переменными составляющими токов (зависимые величины), имеют размерность проводимостей.
Значения y- параметров биполярного транзистора удобнее определять не из вольт-амперных характеристик, а из полученных ранее значений h- параметров:
 (14)
(14)
Подставив в выражения (14) найденные нами значения h- параметров, получим 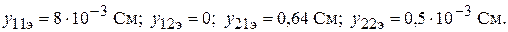
Методические указания к решению задач 21–30
Для схемы, представленной на рис. 11, найдем потенциалы всех узлов и токи всех ветвей. Исходные данные: J = 1 А, Е = 1 В, R 1 = 1 Ом, R 2 = 2 Ом, R 3 = 4 Ом, R 4 = 5 Ом, R 5 = 8 Ом, R 6 = 10 Ом.
| Рис. 11. Схема для проведения статического анализа | 
|
Обозначим узлы схемы номерами от 0 до 3 (узлы, находящиеся справа от узлов 2 и 3, мы никак не обозначили, поскольку они имеют такие же потенциалы). Приравняем потенциал одного из узлов схемы (узла 0) к нулю, а для всех оставшихся узлов составим систему уравнений по методу узловых потенциалов:
 (15)
(15)
где g 1, g 2, g 3, g 4, g 5, g 6 – проводимости ветвей с сопротивлениями R 1, R 2, R 3, R 4, R 5, R 6 соответственно (g = 1/ R).
Решаем данную систему уравнений любым из известных способов. Если число неизвестных больше двух, как в данном случае, систему удобнее решать не методом подстановки, а матричным методом (методом Крамера). В матричном виде система уравнений (15) будет выглядеть

Найдем сначала определитель матрицы проводимостей:
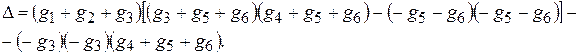
С учетом приведенных значений сопротивлений и параметров источников J и E имеем D» 0,238 См3.
Для определения потенциалов узлов j1, j2 и j3 необходимо предварительно найти определители матриц, полученных из матрицы проводимостей путем подстановки столбца с источниками токов вместо первого, второго и третьего столбцов матрицы соответственно:
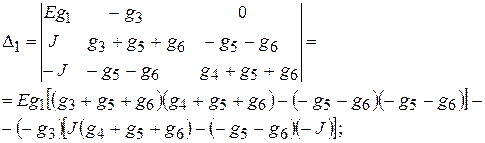
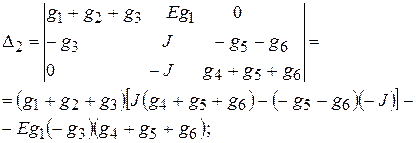
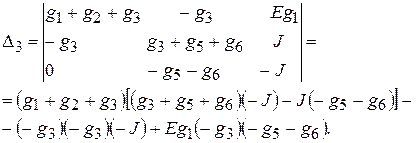
Подставив известные значения проводимостей, E и J, получим D1» 0,2 В×См3, D2» 0,46 В×См3, D3» – 0,32 В×См3. Теперь можно найти потенциалы узлов схемы:
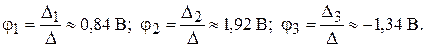
Зная потенциалы узлов схемы, можно определить также и токи ветвей. Обозначим токи, протекающие через резисторы R 1, R 2, R 3, R 4, R 5, R 6, соответственно IR 1, IR 2, IR 3, IR 4, IR 5, IR 6. Тогда, с учетом показанных на рис. 11 направлений токов, их значения можно определить как



Полученное отрицательное значение тока IR 4 означает, что его истинное направление противоположно показанному на рис. 11.
Проверим правильность решения с помощью Первого закона Кирхгофа: для любого узла схемы сумма всех втекающих в него токов должна быть равна сумме вытекающих. Так, например, для узла 2 должно выполняться равенство IR 1 + IR 3 = IR 2. Действительно, 0,16 + 0,27 = 0,43 ≈ ≈ 0,42 А. Небольшая погрешность, связанная с округлениями промежуточных и конечных результатов, вполне допустима.
Аналогично можно удостовериться в выполнимости Первого закона Кирхгофа и для остальных узлов схемы.
Методические указания к решению задач 31–40
Проведем частотный анализ показанной на рис. 12 схемы: получим выражения для амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик его коэффициента передачи по напряжению ku. Исходные данные: R 1 = 2 кОм, R 2 = 1 кОм, R 3 = 10 кОм, С = 1 мкФ. Операционный усилитель будем считать идеальным.
| Рис. 12. Схема для проведения частотного анализа | 
|
При малосигнальном анализе, в том числе и в диапазоне частот, идеальный операционный усилитель (ОУ) обычно представляют как источник напряжения, управляемый напряжением (рис. 13), с бесконечным входным сопротивлением. При этом часто считают выходное сопротивление r вых равным нулю, а коэффициент передачи дифференциального (разностного) входного напряжения k д – стремящимся к бесконечности. Вследствие этого, если для схемы с идеальным операционным усилителем записать систему уравнений по методу узловых потенциалов, то в уравнении для узла, к которому подключен выход ОУ, потенциал этого узла будет умножаться на сумму подключенных к нему проводимостей, одна из которых бесконечна. Поэтому при составлении уравнений по методу узловых потенциалов уравнения для узлов, к которым в схеме подключены выходы операционных усилителей, не записываются. Так как при этом число уравнений станет меньше числа неизвестных потенциалов узлов на количество ОУ в схеме, система станет неразрешимой. Поэтому ее дополняют уравнениями вида φи = φни, где φи, φни – потенциалы инвертирующего и неинвертирующего входов ОУ (это уравнение также вытекает из предположения об идеальности операционного усилителя).

| Рис. 13. Схема замещения идеального операционного усилителя |
С учетом этих особенностей составим систему уравнений по методу узловых потенциалов для схемы, представленной на рис. 12:
 (16)
(16)
где pC – изображение емкостной проводимости YC = j ω C (по Лапласу).
Нам необходимо получить зависимость от частоты коэффициента передачи схемы по напряжению ku, который определяется как отношение выходного напряжения схемы к входному:

Заменив в системе (16) потенциал φ1 на равный ему φ2, получим
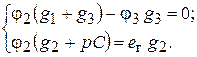
Данную систему удобно решить методом подстановки, выразив из второго уравнения φ2 через e г и подставив затем это выражение вместо φ2 в первое уравнение. Тогда
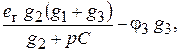
или
 .
.
Отсюда
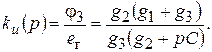
Произведя замену p на j ω, получим зависимость коэффициента передачи по напряжению от комплексной частоты:
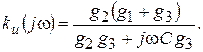 (17)
(17)
На практике вместо выражения (17) пользуются зависимостями от частоты отдельно модуля и аргумента коэффициента передачи – АЧХ и ФЧХ. Пусть в общем случае схемная функция (в нашем случае это коэффициент передачи по напряжению) представлена в виде
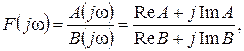
где Re A, Im A – реальная и мнимая части числителя схемной функции;
Re B, Im B – реальная и мнимая части знаменателя схемной функции.
Тогда модуль схемной функции (АЧХ) будет определяться как

а ее аргумент (ФЧХ) – как

В нашем случае выражением для АЧХ будет

а выражением для ФЧХ –
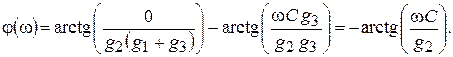
С учетом приведенных параметров элементов схемы имеем
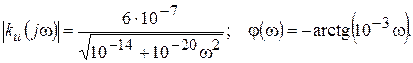 (18)
(18)
Построим качественно АЧХ и ФЧХ для нашего примера (рис. 14). Подставим в выражения (18) частоту ω = 0. При этом модуль коэффициента передачи будет равен 6. Это означает, что на нулевой частоте (на постоянном токе) схема усиливает входное напряжение e г в 6 раз. Угол фазового сдвига φ на нулевой частоте равен нулю.
Исследуя выражения (18), можно увидеть, что при ω → ∞ модуль коэффициента передачи стремится к нулю, а фазовый сдвиг – к углу -π/2.
Частота, на которой модуль коэффициента передачи уменьшается в 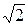 раз от своего максимального значения, т.е. в данном случае равен
раз от своего максимального значения, т.е. в данном случае равен 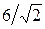 , называется граничной. Приравняв модуль коэффициента передачи к
, называется граничной. Приравняв модуль коэффициента передачи к 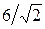 , получим, что граничная частота в нашем случае ωгр = 103 с-1. Угол фазового сдвига на этой частоте, как видно из выражения (18) для φ, равен -π/4.
, получим, что граничная частота в нашем случае ωгр = 103 с-1. Угол фазового сдвига на этой частоте, как видно из выражения (18) для φ, равен -π/4.

Рис. 14. Амплитудно-частотная (а) и фазо-частотная (б) характеристики коэффициента передачи по напряжению схемы на рис. 12
Методические указания к решению задач 41–50
Исследуем приведенную на рис. 12 схему на устойчивость с помощью критериев Гурвица и Михайлова.
Устойчивыми называются системы (цепи), в которых токи и напряжения после снятия внешнего воздействия с течением времени уменьшаются до нуля (затухают).
Неустойчивыми называют системы (цепи), в которых токи и напряжения по окончании действия внешнего возмущения продолжают возрастать. В реальных цепях неустойчивость вызывает самовозбуждение, т.е. генерацию нежелательных колебаний.
Анализ и расчет схем на устойчивость занимают в теории и практике применения электронных цепей очень важное место. Одна из глобальных целей расчета схем − обеспечить устойчивую работу соответствующих цепей в реальных условиях эксплуатации. Невыполнение указанной цели характеризует некачественность проведенных расчетов.
Анализ схемы на устойчивость проводят различными способами, основанными на анализе знаменателя схемной функции и отличающимися характером критерия. Среди них алгебраический критерий устойчивости Гурвица, частотный критерий устойчивости Михайлова, позволяющий судить об устойчивости по виду частотного годографа, и др.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 2457; Нарушение авторских прав?; Мы поможем в написании вашей работы!