Глоссарий 3 страница. 3.2.4.3 Зерттеліп жатқан белгінің деңгейіндегі өзгешеліктерді айқындау

3.2.4.3 Зерттеліп жатқан белгінің деңгейіндегі өзгешеліктерді айқындау.

3. Бұл жерде біз ДА сызбалық қарастырамыз, ол ерікті (т) санының деңгейінде зерттеледі. Бұл жағдайда А фактор қарастырып жатқан деңгейде қандай мәнге ие болғаны маңызды емес, яғни бұл деңгейлер қалай анықталғаны маңызды емес, тек ол екі мәнді болмаса болды. Деңгейлердің бәрә ретінде А факторының болмауын да айтуға болады. Осында ДА екі жағдайын қарастырайық әр деңгейдегі параллелді сынақ саны бірдей және әр түрлі болған жағдайда. Қайталмалы сынақтардың бірдей саны болғанда біз тәжірибенің келесі сызбасына ие боламыз т*п, мұнда т - А_j (j= 1,2,3,... т) факторларының деңгейлерінің саны және п - әр j деңгейіндегі параллелді сынақтар саны. Бұл сызбаның нәтижесі 6.2.1 кестесіне енгізілген. Ең алдымен деңгейлердегі дисперсиялардың тұрақтылығына көз жеткізу керек, ол үшін Бартлетт немесе Кохран бағамдарын қолдану керек.

Егер дисперсиялар тұрақты болмаса, оларды тұрақтандыру керек. Ары қарай жалпы дисперсия жиынтығын бөліктерге бөлуден тұрады, яғни деңгей ішіндегі және деңгей аралығындағы сәйкес тарату, бұл теңдеуге сәйкес (6.1.1) анықтау керек. Ол үшін белгілі квадраттардың соммаларының қатынасын есептеп анализдеу керек, квадраттар соммасы 6.2.1 кестесінде берілген.

Сұрыптаудың жалпы дисперсиясы 6.2.1 кестеде көрстеілген, ол былай анықталған:

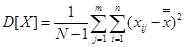(6.2.1)

Екі сомманы (6.2.1) формуласына салайық, бөліктерге бөлейік, олардың біреуі ішкі деңгейдегі (6.2.1 кестедегі бағана) таралу, ал басқасы –деңгейлер арасындағы таралу. Бұл бөліну келесі теңдеумен берілген:

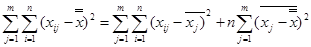(6.2.2)

Бұл теңдеудің бөліктерін түрлендіріп және мәндер енгізіп ауытқушылықтардың квадраттар соммасын есептеуге арналған формулаларды аламыз:

(6.2.3) теңдуінен әр уақытта:

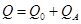(6.2.4)

Сонымен, тиісті дисперсиялар алу үшін, теңдіктің әр бөлігін тәуелсіздік дәрежесінің санына бөліп шығамыз. Бірақ алдымен көп таралған бір қатені талдайық.

Дисперсиялық анализдің негізін қалаушы р.Фишер дисперсияны есептеуді, олардың тәуелсіздік дәрежелерін ескере жүргізеді, сонымен:

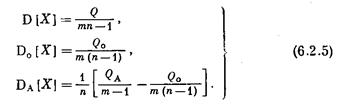
Мұндай дисперсия кезінде жалпы дисперсия бұл орташа арифметикалық кездейсоқ және факторлық дисперсиялардың тәуелсіздік дәрежесінің саны бойынша есептелген:

т≥2 және п≥2 кезінде D₀ [X] және D_А[X] алдындағы бөлшектік көбейткіштер (6.2.6) теңдеуінде әрдайым бірден төмен, яғни әр қашан

D [X] < D₀[X]+ D_А[X]

Және дисперсиялық анализдің негізгі теңдеуі (6.11.) теңдеуі бұзылады. Бірақ айта кету керек, жалпы дисперсия дұрыс есептелді. Осыдан Фишер әдістемесі бойынша D₀[X] және D_А[X] мәндері жоғары болады. Өкінішке орай математикалық статистика бойынша кітаптарда Фишер әдісі бойынша есептеу беріледі. Осыны ескере отырыпФишер әдісі бойынша шығарылған мысалдарды қарастырайық, ал содан соң ДА негізгі теңдеу бұзылмайтындай ДА нәтижелері кесте түрінде беріледі, онда нұсқау түрі, ауытқу квадраттарының соммасының мәні,(6.2.3) теңдеуіне сай, тәуелсіздік дәрежесінің саны, мүмкін дисперсия және (жиі) Ғ-бағамның мәні, сенімді мүмкіндік беріледі.

Фишер әдістемесі бойынша ДА нәтижелері 6.2.2 кестесінде көрсетілген. 6.2.3 кестесінде түзетілген әдіс бойынша есептелген дисперсия нәтижелері берілген.

Бұл әдістер бойынша ерекшеліктер дисперсияны есептеу және дисперсиялық қатынасты тексеруде тұрады, олар ауытқудың квадраттарының соммасын есептеуге әсер етпейді.

Дәріс №4.Өзін-өзі тексеру сұрақтары немесе тесттер

1.Психологиялық зерттеулердің детерминизм принципі.

2.Психологиялық зерттеулердің физиологиялық пен психикалықтың бірлігі принципі.

3.Психологиялық зерттеулердің сана мен іс-әрекет бірлігі принципі.

4.Психологиялық зерттеулердің объективтілік принцип.

5.Психологиялық зерттеулердің даму принципі мен жүйелі-құрылымдық принциптер

3.2.5 Дәріс №5. Дәрістің атауы. Тәуелсіз таңдамалар үшін Стьюденттің T-критерийі

1,Стьюдент критерийінің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

3.2.5.1 Сұрақ атауы 1 Стьюдент критерийінің жалпы тағайындалуы.

1. Тәуелді таңдауларға мысалы сол бір ғана топтың сыналушыларының тәуелсіз өзгергіштіктердің әсерге дейін және кейінгі нәтижелері жатады. Біздің жағдайда тәуелді таңдау үшін статистикалық әдістердің көмегімен жеке эксперименттік топ үшін жеке тексеру тобы үшін фондық деңгеймен әсерден кейінгі деңгейдің арасындағы айырмашылықтың дәл екендігі жайлы гипотезаны тексеруге болады. Тәуелді таңдау үшін орташалардың айырмашылықтарының дәлдігін анықтау үшін келесі формула қолданылады:

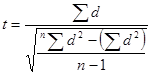
мұнда d әрбір жұптағы нәтижелердің арасындағы айырма, åd осы жеке айырмалардың суммасы, åd² жеке айырмалардың квадраттарының суммасы.

Алынған нәтижелер кестедегі t мәнімен тексеріледі, онда n-1 еркіндік дәрежесіне ие мәнді іздейміз; бұл жағдайда n жұп мәліметтердің саны болып табылады. Формуланы есептемес бұрын әрбір топ үшін барлық жұптардың нәтижелерінің арасындағы жеке айырмалар, осы айырмашылықтардың әрқайсысының квадраты, осы айырмашылықтардың суммасы, олардың квадраттарының суммасы есептелінеді. Ол үшін келесі операцияны жүзеге асыру керек.

Тексеру тобы. Фон және әсерден кейінгі нәтижелерді салыстыру.

Сыналушылар	Фон	Әсерден кейін	d	d^2
Қ1			+2
			-2
			+1
			-2
			+3
			-2
			-2
У1			+2
			+1
			-	-
			+1
			+1
			-3
			-	-
			+3
åd=+3	åd^2=55

t=0,39 болады, осы t=0,39 деген шамасы 0,05 мәнділік деңгейінде 14 еркіндік дәрежесінде ол кіші болып тұр, басқаша айтсақ t үшін ықтималдылық табалдырығы 0,05 жоғары. Сөйтіп нөлдік гипотеза жоққа шығарылмайды, таңдаулар арасындағы айырмашылық дәл емес. Оны келесі жолмен көрсетуге болады:

t=0,39; h=14; р>0,05 дәл емес.

Енді өзіңіз эксперименттік топ үшін екі бөлуге сәйкес тәуелді таңдау үшін Стъюдент әдісін қолданып көріңіз, жеке айырмашылықтарды есептегенде жұптар үшін келесі нәтиже алынуы керек:

åd=-59; åd²=349

Бұл параметрлік әдіс бірдей вариансаға ие болатын, нормалды бөлуге сәйкес келген популяция жайлы сандық мәліметтерді талдауда олардың орташаларының арасындағы айырмашылықтар дәл болады деген гипотезаны тексеруүшін қолданылады.

3.2.5.2 Сұрақ атауы 2 Әдістің шектеуліктері

2. Алайда Стъюдент әдісі өкінішке орай аз мөлшерлі таңдауларда көп қолданылады, алдын ала популяциядағы мәліметтер нормалды бөлуге бағынады деген жағдай тексерілмейді (мысалы, тапсырма өте жеңіл болып оны барлық сыналушылар тез бірдей орындайды немесе керісінше барлық сыналушылар қиын тапсырмаларды бірдей орындай алмайды бұл жағдайлар нормалды бөлуді бере алмайды).

Стъюдент әдісі тәуелді және тәуелсіз таңдаулар үшін айырмасы болады. Тәуелсіз таңдаулар сыналушылардың екі түрлі топтарын зерттеуде алынады (біздің экспериментте ол тексеру тобы мен эксперименттік топ). Тәуелсіз таңдау жағдайында орташалардың айырмашылығын талдау үшін келесі формула қолданылады:

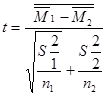
мұнда М1 – бірінші таңдаудың орташа мәні, М2 – екінші таңдаудың орташасы, s1 – бірінші таңдау үшін стандартты ауытқу, s2 – екінші таңдау үшін стандартты ауытқу; n1- n2- бірінші және екінші таңдаудағы элементтер саны.

Енді мәнділігі бойынша дайын кестеден t шамасын табамыз, ол еркіндік дәрежесін n2 бойынша табамыз, n екі таңдаудағы сыналушылардың жалпы саны және ол шаманы формула бойынша есептелген шамамен салыстырамыз.

Егерде алынған нәтиже 0,05 дәлдік деңгейі бойынша кестеден алынған мәнге қарағанда үлкен болса онда нөлдік гипотеза қабылданбайды, альтернативті гипотеза қабылданады, яғни орташалардың арасындағы айырмашылықтар дәл деп саналады.

Керісінше егерде кестеден алынған шамадан алынған нәтиже аз болса онда нөлдік гипотезаны жоққа шығаруға болмайды, ендеше орташалардың арасындағы айырмашылық дәл емес деп саналады.

Біз жоғарыда келтірген гипотетикалық эксперимент нәтижелері бойынша t есептесек ол t=0,53 тең болады, осыны кестедегі t мәнімен салыстырамыз да мына қорытындыға келеміз: біз алған t=0,53 шамасы 0,05 мәнділік деңгейінде 26 еркіндік дәрежесі үшін аз болады, сондықтан да ықтималдылық деңгейі t 0,05-тен жоғары болады және нөлдік гипотезаны жоққа шығаруға болмайды; сөйтіп екі таңдау арасындағы айырмашылық дәл емес, яғни олар міндетті түрде бір популяцияға жата алады:

t=0,39; h=14; р>0,05 дәл емеc (недостоверно).

Жоғарыда айтқанымыздай бұл жағдайда таңдау шамасы өте үлкен болмағандықтан, ал эксперименттік топтың әсерден кейін алынған нәтижелері нормалды бөлуге сәйкес келмегендіктен ең дұрысы параметрлік емес әдістер қолдану керек, мысалы Мана-Уитни және басқалар.

Алайда t тест біз әсерден кейінгі эксперименттік және тексеру топтарының нәтижелерінің арасындағы арасындағы орташалардың айырмашылықтарының дәлдігі жайлы гипотезаны тексеруге пайдалы болады. Бұл жағдайды өздеріңіз тауып салыстыруға болады.

3.2.5.3 Сұрақ атауы 3 Әдістің шектеуліктері.

3.Психологияда сандық өңдеудің тағы бір түрі әртүрлі статистикалық жиынтықтардың екі орташа мәндерінің мәнділіктерін тексеруде Стъюдент критерийін (Госсет) қолдану, орташа мәндердің айырмашылықтары статистикалық мәнділікке тексерілетін таңдаудағы нормалды бөлуді береді:

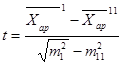
мұнда 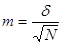орташа қате деп аталады, 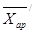және 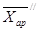айырмашылықтары тексерілетін арифметикалық орташалар, орташа қателер. №1-2 мысалдарды критерийлерін есептеп, салыстырамыз:

N^/=35 N^//=30

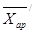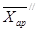=3,6 =9,1

d^/=1,03 d^//=1,83

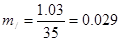
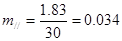
Бұл мәнді дайын кестемен салыстырамыз. Онда «еркіндік дәрежсі» есептелінген, ол былай анықталады:

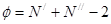
Біздің жағдайда j= 35+30-2=73

Кесте бойынша мәнділіктің 5% деңгейінде t мәні, тіпті 80 үшін 1,99 тең. Ендеше №1-2 мысалдардың орташа мәндерінің айырмашылықтары статистикалы мәнді емес, яғни алынған мәндер дәл емес. Бұл критерий екі орташаның жақындық дәрежесін бағаламайды, ол жақындықты кездейсоқ деп санау үшін қарастырады.

Дәріс №5.Өзін-өзі тексеру сұрақтары немесе тестер

1.Психологиялық зерттеу әдістерінің Пирьов, Ананьев, Дружинин бойынша классификациялау.

2.Психологиялық зерттеу жұмысында зерттеушіге қойылатын этикалық талаптар

3.Психологиялық ғылыми зерттеу жұмыстарының құрылымы туралы түсінік.

4.Проблеманы анықтау.

5.Гипотезаны ұсыну.

6.Гипотезаны тексеруді жүзеге асыру.

3.2.6 Дәріс №6. Өзгешеліктер статистикасы. Манна-Уитнидің U – критерийі

1.Критерийінің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

3.2.6.1 1. Критерийінің жалпы тағайындалуы.

1. Негізгі ұғымыдары белгілері мен ауыспалары - өлшегіштік құбылыстар сандық өлшенетін белгілі бір белгінің деңгейі бойынша 2 таңдау (выборка) арас-ғы өзгерістерді бағалау үшін қолданылады. Егер n₁*n₂ ≥3 және n₁=2, n₂≥5 болса және кіші таңдағандар арасында өзгешеліктерді анықтауға мүмкіндік береді.

Қиылысатын мағыналар облысыта неғұрлым кіші болса, өзгешіліктер соғұрлым дәл болады, яғни U қатарлар (тез таңдау өзгешелігі) арасындағы ұқсастықтардың неғұрлым үлкенін көрсетеді. Сондықтан

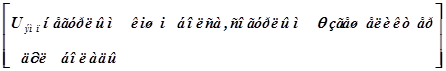
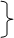Н₀: 2 топтағы белгілер деңгейі 1 топтан төмен

Н₁: 2 топтағы белгілер деңгейі 1 топтан төмен гипотеза

Шектер:

Әрбір таңдауда 3 бақылаудан кем болмау керек: n₁*n₂ ≥3. Бірақ І-де 2 болса, ІІ-де 5-тен кем болмауы керек.

60-тан артық болмау керек: n₁*n₂ ≥60. Бірақ n₁*n₂ ≥20 болғанда өте қиын болады.

Рангілеу:

Ең төменіне 1 ранг (ең төмен) берілген. Ең жоғарғысына ең үлкен ранг берілген. Мысалы: n₁=э болса ең үлкен ранг. Егер бірнеше мағыналар бірдей болса, онда олардың ортақ көрсеткіші шығады. Рангтердің ортақ саны (расчетной) сәйкес б.к => Ол анықт:

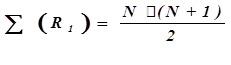N-рангінің мағыналарның жалпы саны

(М, 2 мағына 12 сек. тең. Олар 4 және 5 берілу керек

3.2.6.2 Сұрақ атауы 2.Анализ алгоритмі.

2. Алгоритм

Зерттеулер нәтижесінен инд-ды карточкаларға жазу.

1 таңдау – бір түс (қызыл); 2 таңдау – ІІ түс (көк)

1 ортақ (түсіне қарамай) ретке өсу, не кему ретімен орнату

Карт-рды рангілеу (ранг бойынша) (n₁+n₂)

2 қатарға (көк-қызыл) бөлу

Әр қатар бойынша ранг жиынын есептеу (должна совпадать с расчетной)

2 рангілі соммадан үлкенін табу

U табу

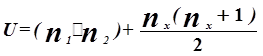
n₁ - 1-таңдаудағы ад. саны

n₂ - 2-таңдаудағы ад. саны

Т_х - 2 ранг санм. үлкені

n_х – рангілер соммасы үлкен топтың ад. саны

U таблица бойынша табу

Егер U_эмп > U_{кр 005}, онда Н_о қаб.

Егер U_эмп > U_{кр 005}, онда Н_о қабылдм.

&&&

$$$002-006-003$3.2.6.3 Сұрақ атауы 3.Әдістің шектеуліктері

3. => 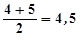Инверсия сан критерийі бұлда сериялы критерий сияқты екі таңдаудың мүшелерінің шамаларының айырмашылығын бағалауға арналған бірақ күші жағынан жоғары.

Бұл критерий Инверсия санын есептеуге арналған. Инверсияның жалпы саны кестемен салыстырылады.

№5-мысалға осы критерийді қолданамыз. Бірінші қадам, сериялы критерийдегідей жалпы реттелген қатарды аламыз, сондықтан да 15 кесте қайталанады.

Кесте 16.

Хі

Уі

n_х=8

Енді инверсия санын есептейміз. Бізде жоғарғы Х_і қатар мүшелер екінші У_і қатарының мүшелеріне қарағанда алда келеді. Сәйкес цифрларды жоғарғы қатардың үстіне орналастыру ыңғайлы. 30,30 сандарының алдында 29 цифры алды да келеді, ендеше жоғарғы жағына І цифрларды қоямыз. Х_і 32 және 33 шамаларының алдына У_і екі саны алдында келеді, сондықтан да /29 және 31/32 мен 33 үстіне 2 цифрлар қойылған. Ал 37 саны үшін төменгі қатардың 5 цифры алды да, ендеше оның үстіне 5 қойылады: Инверсияның жалпы саны: И=1+1+2+2+5=11 Кестемен салыстырсақ И /8,7/=12 яғни 5/ деңгейі үшін ерлер мен әйелдердің табалдырықтарының шамаларының айырмашылықтары статистикалы мәнді.

Дәріс №6.Өзін-өзі тексеру сұрақтары

1.Психологиялық зерттеу жұмысында зерттеушіге қойылатын этикалық талаптар

2.Психологиялық ғылыми зерттеу жұмыстарының құрылымы туралы түсінік.

3.Проблеманы анықтау.

3.2.7 Дәріс №7. Өзгешеліктер статистикасы. Крускал-Уоллистің Н – критерийі

1.Критерийінің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

$3.2.7.1 Сұрақ атауы 1. Критерийінің жалпы тағайындалуы.

1. Белгілі бір белгі бойынша 3, 4 және т.б таңд-лар арасыеда өзгеш-рді бағалау үшін қолданылады. Белгі деңгейінің топтан топқа өту кезінде өзгерулерін білдіреді.

Н₀: 1, 2, 3 таңдаулар арасындағы белгі бойынша кездейсоқ өзгерулер бар

Н₁: Кездейсоқ өзгерулер бар

Шектеулер:

3 таңд-ды сәйкестендіру кезінде біреуінде ъ болса, ал қалған 2-де n=2 болса жоғары деңгейде салыстыру үшін әрбір таңдауда 3 бақылау болу керек немесе 4:2:2 болу керек.

Н кр-нің критикалық мағыналары 3 таңдауға арн. Оларды кесте кесте бойынша қарау керек. Егер таңдаулар көп болса, онда х² критериі бойынша қарау керек. V=c-1 (еркіндік деңгейлерінің саны) с – сәйкестік таңдаулар саны.

3.2.7.2 Сұрақ атауы 2 Анализ алгоритмі.

2. Алгоритм.

Инд. картаға жазу

Әр топты 1 түске бөлу (көк, сары, жасыл)

Түсіне қарамай 1 топқа жіктеу

Рангілеу. Әр карт-ға сәйкес рангі жазу. Рангілеудің жалпы саны = орт. таңд-ғы ад. саны

Түске байланысты топтарға бөлу

Әр топтың ранг жиынын есептеу.

Н табу:

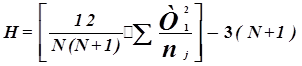
N – жалпы ад. саны

n - әр топтағы ад. саны

Т - әр топ бойынша ранг соммасы

8. а) с=3, n₁* n₂*n₃ ≤ 5 болса кесте бойынша анықт. (IV)

Н_эмп≥ Н_0,05 Н₀ қабылдм.

б) с>3, n₁* n₂*n₃ > 5 болса х² (ІХ) бойынша анықт.

Н_эмп≥ х² Н₀ қабылдм.

3.2.7.3 Сұрақ атауы 3. Әдістің шектеуліктері.

3. Белгілер критерийлері. (G)

Зерт-тін белгінің ауысуы бағытын анықтау. Сапалы немесе сандық ауысуларға да қолд.

Н₀: Ауысу бағытының (типичный) түрінің басымдылығы кездейсоқ.

Н₁: Кездейсоқ емес

Дәріс №7.Өзін-өзі тексеру сұрақтары

1.Гипотезаны ұсыну.

2.Гипотезаны тексеруді жүзеге асыру.

Дәріс №8. Дәрістің атауы. 8. Зерттеліп жатқан белгінің деңгейіндегі ығысуларды айқындау. Байланысты таңдамалар үшін дисперсионды анализ.

1.Байланысты таңдамалар үшін дисперсионды анализдің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері.

&&&

$$$002-008-001$3.2.8.1 Сұрақ атауы 1. Байланысты таңдамалар үшін дисперсионды анализдің жалпы тағайындалуы.

1 Дисперсиялық анализдің негізін қалаушы р.Фишер дисперсияны есептеуді, олардың тәуелсіздік дәрежелерін ескере жүргізеді, сонымен:

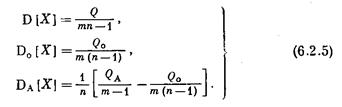
Мұндай дисперсия кезінде жалпы дисперсия бұл орташа арифметикалық кездейсоқ және факторлық дисперсиялардың тәуелсіздік дәрежесінің саны бойынша есептелген:

т≥2 және п≥2 кезінде D₀ [X] және D_А[X] алдындағы бөлшектік көбейткіштер (6.2.6) теңдеуінде әрдайым бірден төмен, яғни әр қашан

D [X] < D₀[X]+ D_А[X]

Және дисперсиялық анализдің негізгі теңдеуі (6.11.) теңдеуі бұзылады. Бірақ айта кету керек, жалпы дисперсия дұрыс есептелді. Осыдан Фишер әдістемесі бойынша D₀[X] және D_А[X] мәндері жоғары болады. Өкінішке орай математикалық статистика бойынша кітаптарда Фишер әдісі бойынша есептеу беріледі. Осыны ескере отырыпФишер әдісі бойынша шығарылған мысалдарды қарастырайық, ал содан соң ДА негізгі теңдеу бұзылмайтындай ДА нәтижелері кесте түрінде беріледі, онда нұсқау түрі, ауытқу квадраттарының соммасының мәні,(6.2.3) теңдеуіне сай, тәуелсіздік дәрежесінің саны, мүмкін дисперсия және (жиі) Ғ-бағамның мәні, сенімді мүмкіндік беріледі.

Фишер әдістемесі бойынша ДА нәтижелері 6.2.2 кестесінде көрсетілген. 6.2.3 кестесінде түзетілген әдіс бойынша есептелген дисперсия нәтижелері берілген.

Бұл әдістер бойынша ерекшеліктер дисперсияны есептеу және дисперсиялық қатынасты тексеруде тұрады, олар ауытқудың квадраттарының соммасын есептеуге әсер етпейді.

3.2.8.2 Сұрақ атауы 2. Анализ алгоритмі.

2. Сыни нүктелерге жақын Ғ мәндерде Фишер әдістемесі дұрыс нөлдік тұжырымдаманың алып тасталуына және орнына жалған балама тұжырымның қабылдануына әкеле алады, яғни екіншілік түрде қателер мүмкіндігі көп, егер есепті Фишер бойынша жүргізсек.

Дата добавления: 2014-12-25