Глоссарий 4 страница

3.2.8.3 Сұрақ атауы 3. Әдістің шектеуліктері.

3. Қайталмалы сынақтар саны тең болмағанда есептеу схемасы қиындайды. Эксперимент жоспары бар: 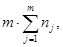мұнда n_j=А факторының j-деңгейіндегі сұрыптау көлемі.

Тәжірибенің нәтижелерін кестеге енгіземіз, алдынғы жағдайдағыдай, бірақ тағы бір n_j мәні қосылады. Ауытқу квадрат соммасының ауытқуын есептеуге арналған формула өзгереді. Ол енді мынандай түрде болады.

Мұнда

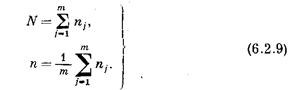
Егер Фишер әдісін қолдансақ, бағаланатын дисперсия бөлшектері ретінде:

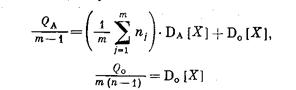
және

Дисперсияны есептеу үшін түзетілген әдісті қолданамыз, ал дисперсиялық қатынасты есептеу үшін Фишер әдісін қолданады.

Дәріс №8.Өзін-өзі тексеру

Фишер әдістемесіне реферат

3.2.9 Дәріс №9. Зерттеліп жатқан белгінің деңгейіндегі ығысуларды айқындау. Байланысты таңдамалар үшін Стьюденттің T-критерийі

1.Байланысты таңдамалар үшін Стьюденттің T-критерийінің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

3.2.9.1 Сұрақ атауы 1 Байланысты таңдамалар үшін Стьюденттің T-критерийінің жалпы тағайындалуы

3.2.9.2 Сұрақ атауы 2.Анализ алгоритмі

3.2.9.3 Сұрақ атауы 3. Әдістің шектеуліктері.

Жаңа әдістеменің құндылығы мынамен анықталады:

Өлшеудің дәлдігін жоғарлатады, сенімділігін арттырады.

Болжанылатын қасиеттер туралы толық сипаттама береді.

Зерттеу уақытын азайтады

Зерттелушілердің санын кеңейту (жас бойынша, білім деңгейі, кәсіби қызметі, психикалық денсаулық жағдайы, дамуы бойынша және т.б)

Нәтижелерді өндеудің оңайлатандыру(жеңілдету, алгоритмге салу)

Бірақ әдістемені кең қолданысқа әр түрлі салада қолдану үшін,оны психодиагностикалық тексеруден толық параметрлері арқылы өткізу керек және өтсе ғана қолдану керек.

Бұл процесс күрделі және ұзақ. Мұндай талаптарды психодиагностиканың аранайы әдебиеттерінде табуға болады. Бірақ ғылыми зерттеу мақсаты үшін, толық психометриялық тексеру әдістемесі болмаса да (анкеталық сұрау) қолданылып, бағалы ақпарат беруде және ғылыми мәнге ие болады.

Дәріс №9.Өзін-өзі тексеру сұрақтары немесе тестер

1.Психологиялық зерттеу жұмысында зерттеушіге қойылатын этикалық талаптар

2.Психологиялық ғылыми зерттеу жұмыстарының құрылымы туралы түсінік.

3.Проблеманы анықтау.

4.Гипотезаны ұсыну.

5.Гипотезаны тексеруді жүзеге асыру.

3.2.10 Дәріс №10. Дәрістің атауы. 10 Ығысулар статистикасы. Вилкоксоның Т – критерийі

1.Критерийдің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

3.2.10.1 Сұрақ атауы 1 Критерийдің жалпы тағайындалуы.

1. 2 түрлі жағдайда бір таңдауда өлшенген көрсет-рді анық-ға қолд. Ол өзгерулердің бағытын және күштілігін (выраженность) көрсет.

Н₀: тиісті (типичный) бағыттағы өзгеріс интен-лігі тиісті е. бағ-ғы өзгер. интен-нен басым е. Н₁: басым. Бұл да бұрынғы критерийлер сияқты жұпты кездесетін жиынтықтардың шамаларын салыстыруға қолданылады, бірақ оларда күші жоғары. Ол тек ғана салыстыратын қатарлардың арасындағы айырманы (таңба) ғана емес ол айырмашылықтардың абсолютті шамаларын да қарастырады.

Бұл критерийді төмендегі №7 мысалға қолданамыз. Төменгі қатардың сандарын жоғарғы қатардан алып тастаймыз, тек айырма таңбаны ғана емесоның шамасын да тіркейміз:

Кесте 14. n=12

Мамандық
Ғылыми абстракция
Айырма	+3	-1			-1	-1		-3
Абсолют шама бойынша айырмашылық рангісі	8,5			8,5			11,5	8,5		8,5	11,5

Енді барлық айырмашылықтарға таңбадан тәуелсіз айырмашылық шамасының өсу реті бойынша олардың рангілерін жазамыз. Осы операцияны түсіндірейік: айырмашылықытң ең кіші шамасы -1, ал мұндай 1 бізде бесеу, ендеше ол мына рангіні береді: 1,2,3,4,5.

Сондықтан да барлық 1-ге тең бір ғана 3 рангісін қоямыз, одан рангінің жалпы саны бес бірдің шамасы өзгермейді.

Содан кейінгі рангі -6, оған 2 шамасын береміз. 7,8,9,10 рангілеріне 3-ң төрт шамасы сәйкес келеді, себебі әрбір төрттік үшін рангі – 11,5 сәйкес. Енді теріс айырмашылықтар үшін Т рангілерінің қосындысын есептейміз:

Т=3+3+3+8,5=17,5

Кесте бойынша критикалық мән Т=17, яғни біздің эмпирикалық мән (0,05 деңгейі) үшін арналған кесте мәндерінен үлкен болды. сондықтан да әртүрлі сапалы сөздерді есте сақтай көлемінің шамаларының айырмашылықтары сыналушылар тобы үшін статистикалы мәнді емес.

3.2.10.2 Сұрақ атауы 2.Анализ алгоритмі.

2. Алгоритм.

Ретке салу (алф. бойынша)

І және ІІ өлшемдегі инд-ды мағын-рды алу. Олардың арасындағы айырмашылықты анықтау.

Айырмашылықтарды абсолютті биіктерге ауыстыру (абс. величина). Бір ретке келтіру.

Бұл абсолюттік өлшемдерді (величины) рангке салу.

«Тиісті е» бағ-қа тән өзгерістерге сәйкес рангтерді дөңгелектеп белгілеу.

Бұл рангтердің соммасын жинау

- жиі емес белгісі бар ранг.

n – ға тән Т-ны табу. Егер Т_эмп≤Т_кр, онда өзгеріс (дәл) шынайы болуы керек.

3.2.10.3 Сұрақ атауы 3 Әдістің шектеуліктері

3. Шектеулер:

2 жағд. өлшем-р өткен ад. саны≥5; max=50

О-к өзгер-р қарастырылм.

Дәріс №10.Өзін-өзі тексеру сұрақтары

1.Салыстыру әдісінің негіздері.

2.Лонгитюд әдісінің негіздері.

3.Тігінен және көлденең кесу ұғымдары.

5.Комплексті әдістерінің негіздері.

3.2.11 Дәріс №11. Дәрістің атауы. 11. Ығысулар статистикасы. Фридманның χ2r Критерий і

1.Критерийдің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері.

3.2.11.1 Сұрақ атауы 1 Критерийдің жалпы тағайындалуы.

1. Эксперименттік зерттеудің нәтижесін өңдеуде алғашқы (бірінші) статистикалық берілгендер тәсілі пайдаланылады: іріктелген арифметикалық орташа мәнді (эксперименттегі психологиялық қасиеттің орташа бағасының көрсеткіші) дисперсия деп аталады. Ол іріктелген жиілік арасындағы таңдамалы стандартты ауытқулардың орташа арифметикалық мәндерін сипат тайды. Мұндай есептеулер көрсеткіштердің көмегімен эксперименттен алынған нәтижелерді математикалық тұрғыдан бағалау үшін пайдаланылады. Алғашында берілгендерді өңдеуде жиі қолданылатын орталық тенденция өлшемін іріктелген арифметикалық шаманың орташа Х мәнімен анықталды. Орташа арифметикалық іріктелген мәні бастапқы шамаларды біртіндеп біріктіру арқылы есептеледі. Ол қосынды санды жалпы алынғандардың N санына бөлу арқылы төменде келтірілген теңдікпен анықталады

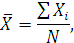
мұнда: – сандық көрсеткіштердің қосындысы;

N – іріктелген топтар саны.

Нәтижелердің өлшемдік өзгергіштері, кейбір шаманың орташа арифметикалық аумағында шашылу дәрежесін сипаттаушы ретінде, дисперсияны және таңдамалы стандарттық ауытқуларды есептеу былайша жүргізілді:

1. Орташа арифметикалық (О.А.) шама () есептелді,

2. Әр өлшенген (Х)-тен нәтиженің ауытқуы (О.А.) табылады

X=X_i - .

3. Іріктелген нәтиженің таңдамалы орташа мәнін квадратталынды

Х^2.

4. Әр нәтиженің ауытқу квадратының қосындысы табылды

.

5. Ауытқу квадратының қосындыларын, жалпы іріктелген топтардың N санына бөліп, дисперсия шамасы Д есептелінді

,

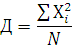
6. Квадрат түбірінен дисперсияны шығарып іріктелген мәндердің S стандарттық ауытқуы анықталды

.

7. Эксперименттік әдістеменің дұрыстығын шығарып іріктелген тексеруге және дәлелдеуге екінші (қайтара) статистикалық өңдеу әдістемесі, яғни χ² –критерий («хи квадрат критерий») көрсеткіштері пайдаланылды.

8. Ол көрсеткіш келесі теңдікпен анықталды

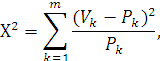
мұнда: Р_к – констатациялы эксперименттің топқа бөлінген көрсеткіштер жиілігі;

V _k – дамытатын эксперименттен кейінгі топқа бөлінген көрсеткіштер жиіліктері;

m – қарастырылған нәтижелердің топқа бөлінген жалпы саны.

Мұндағы Р_к және V _k жиіліктері анықталды.

Эксперименттерге Семей қаласының №15 жалпы білім беретін орта мектептің 8-9 сынып оқушылары қатысты. Эксперимент барысында 10 ұпайлық көлемінде анықталған сыналушылардың зейін қасиеттерінің көрсеткіштері анықталды.

Мысалы, 1-ші экспериментке қатысқан екі сыналушы – 9 ұпай, он бір сыналушы – 8 ұпай, он сыналушы – 7 ұпай, төрт сыналушы – 6 ұпай жинаған.

Онда P_k 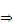2, 11, 10, 4 топтарына бөлінген сыналушылардың жиілік мәндеріне ие болады.

Дамытатын экспериментте 10 ұпай көлемімен анықталып, сыналушылардың зейін қасиеттерінің ұпайлық көрсеткіштері деректерінен алынды.

Мұнда дамытатын экспериментке қатысқан:

сегіз сыналушы – 10 ұпай,

он үш сыналушы – 9 ұпай,

бес сыналушы – 8 ұпай,

бір сыналушы – 7 ұпай жинаған, ал 6 ұпай жинаған ешкім болмады.

Онда V _k 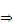8, 13, 5, 1 топтарына бөлінген сыналушылардың жиілік мәндеріне ие болады. Бостандық дәрежесінің саны m - 1 = 4 - 1 = 3.

Осы анықталған мәндерді пайдаланып χ² критерийінің деңгейі анықталады

,

.

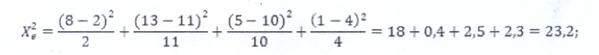
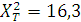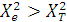χ²-ның эксперименттік есеп мәні кестедегі мәнінен көп болғандықтан және жіберілген қате 1%-дан аз болады деп қабылдағанда дамытатын эксперименттің нәтижелік жорамалы орындалды деуге болады.

3.2.11.2 Сұрақ атауы 2 Анализ алгоритмі.

2. Жалпы, өлшемдік емес Хи-квадрат әдісін қолдану үшін орташа немесе стандартты ауытқуды есептеуді қажет етпейді. Оның артықшылығы сол оны қолдану үшін екі өзгергіштіктен алынған нәтижелерді бөлу жиілігін ғана білу қажет болады. Сондықтан бұл статистикалық әдіс сапалы мәліметтерді өңдеуге арналады.

3.2.11.3 Сұрақ атауы 3 Әдістің шектеуліктері.

3. Аталмыш әдістеме эмпирикалық функциялардың қалыпты жіктелуінің сәйкестілігін тексеруге де пайдаланылады. Сонымен қатар әдістеме болжамның бірнеше мүмкіндік мәндерінің нақты теңдіктерін анықтауға мүмкіндік береді.

Хи–квадрат критерийі екі түрлі мақсатта қолданылады:

эмпирикалық жіктелуді теориялық теңдік, қалыпты немесе басқа да өлшемдермен салыстыру үшін, екі, үш немесе одан да көп эмпирикалық жіктелулерді бір ғана белгісі бойынша салыстыру үшін.

Дәріс №11.Өзін-өзі тексеру

1.Ауызша, жазбаша, еркінсауалнамалардың айырмашылығы неде.

2. Эксперимент түрлері ата.

3. Бақылау формалары ата.

3.2.12 Дәріс №12. Дәрістің атауы. Номиналды шкалалардағы өзгешеліктер статистикасы. Пирсонның χ2 критерий

1.Критерийдің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

&&&

$$$002-012-001$3.2.12.1 Сұрақ атауы 1 Критерийдің жалпы тағайындалуы.

1. Пирсонның корреляциялық коэффициенті қолданылады: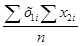

мұнда бірінші өлшеудегі сыналушының тест балы, сол сыналушының қайталанған өлшеудегі тест балы, сыналушылар саны.

Индивидтің тест балының «шын» мәнін есептеу формуласы:

мұнда Х¥ - шын балл, Хі – сыналушының эмпирикалық баллы, r-тестің эмпирикалық өлшенген сенімділігі, х – тест үшін орташа мән. Ретестілік сенімділікті тек индивидтердің психикалық сипаттамаларына қатысты қолданады. Ал тест эмоциялық күйге қатысты құрылса, онда ретестік сенімділік жарамайды. 2 максималды қолд:

- белгілеушінің эмп-қ және теор-қ үлестірулерін салыст-ға

- белгілі бір белгіге тән 2,3 не одан да көп эмп-қ үлестірмелерді салыст.

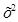критерий эмп-қ және тео-қ үлестірмелерде белгілерінің түрлі мағыналары бірдей жиілікпен кездесе ме деген сұрақ жауап береді. Түрлі шкалада ұсынылған белгілерді в салыстыруға мүмкіндік береді

Мін-не байланысты гипот-р түрлі бол:

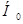: эмп-қ үлест теор-қтан ерекшеленбейді

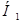: ерекшеленеді

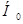: 1 эмп-қ 2 эмп.ү-ден ерекшеленбейді

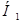: ерекшеленеді

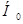: 1,2,3... эмп – қ ү-р өзара ерекшеленбейді

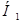: ерекшеленеді

3.2.12.2 Сұрақ атауы 2. Анализ алгоритмі.

2. Алгоритм.

1. Кестеге разряд атын және оған сәйкес эмп-қ жиілікті енгізу

2. әрбір эмп жиіліктің қасына тео-қ жиілікті түзіп шығу (2 баған)

3. 2ас-ғы әрбір разряд бойынша айырмашылықтары санау, жазу (3 баған)

4. Еркіндік деңгейінің санын анық

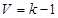
К –разряд саны

5. Алынған айырмашылықтарды квадратқа шығару, жазу (4 баған)

6. алынған квадрат санын тео-қ жиілікке бөлу, жазу (5 баған)

7. 5 бағанның қосындысын табу, оны деп белгілеу

8. Кесте бойынша анықтау.

Егер 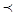кр. мағын., айырм шынайы е

Егер 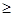кр. мағын., онда шынайы

3.2.12.2 Сұрақ атауы3. Әдістің шектеуліктері

3. Шектеулер:

1. (ад саны) таңдау V –мі

2. әрбір ячейка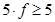

3. белгілердің вариативтік диапазонның меңг керек

Дәріс №12.Өзін-өзі тексеру

Пирсонның χ2 критерийіне мысал әзірлеу

3.2.13 Дәріс №13. Дәрістің атауы. Корреляциялық статистика. Пирсонның корреляциялық коэфициенті.

1.Критерийдің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

3.2.13.1 Сұрақ атауы 1.Критерийдің жалпы тағайындалуы.

1. Орталық тенденция өлшемдері және өзгеру өлшемдері не үшін керек? 1-ден, олар алғашқы мәліметтерді талдау үшін. Орталық тенденция өлшемдері мәндерінің негізінде басқа іріктеудің нәтижелерін табуға болады. Өзгеру өлшемдері негізінде жүргізумен есептеулер дұрыстығын есептеуге болады. 2-ден, бұл өлшемдер айырмашылықтардың статистикалық маңыздылығын тексеруге қажет және де корреляция коэффициенттерін есептеуге қажет.

Өзара қатынас өлшемдері. Корреляция коэффиценттерін 2 айнымалы арасындағы қатынасты және оның деңгейін анықтау үшін қолданады. Корреляция коэффиценті-1 ден +1 ге дейін өзгереді. Бұл аралықта жатқан шамалар салыстырылатын айнымалылардың өзара қатынасын көрсетеді. Егер корреляция коэффиценті 0-ге тең болса, өзара қатынас жоқ. Оң корреляциялық қатынас 2 айналымалылыларар асындағы тура пропорционалдықты, ал теріс – кері пропорционалдықты көрсетеді. Неғұрлым корреляция коэффиценті көп болса, соғұрлым өзара қатынас тығыз болады. Коэффицент + 1 болса, айнымалылар арасындағы теңдік туралы айтуға болады.

Реттік шамаларды салыстырғанды τ,Спирмен бойынша рангілік корреляция коэффицентін (p), интервалды шамаларды салыстырғанда –К.Пирсон бойынша көбейтінділер корреляциясының корреляция коэффицентін қолданады ()ч. Сол коэффиценттерді есептеулерді қарастырайық.

“Иә” немесе “жоқ” жауаптарын талап ететін 2 сұрақтама (х және у) көмегімен алғашқы нәтижелер зерттелушілердің жауаптары (N=15) алынған. Нәтижелері әрбір сұрақтамаға бөлек “иә” жауаптарының қосындысы түрінде алынады. Х және У сұрақтамалары зерттелетін тұлғалардың ұқсас қасиеттерін өлшей ме, жоқ па соны анықтау керек. Егер 2 сұрақтаманың мазмұны мен тұжырымдамаларының бір бірінен айырмашылығы аз болса онда балдарының қосындысы да бір біріне жақын болады.

Пирсон формуласының корреляция коэффициенті алғашқы нәтижелер және орта квадраттық ауытқудың орта арифметикалық мәнінен ауытқу негізінде есептеледі. Ол мынандай:

τxу= Σx*у/Nσx*σу

Мұндағы: х-Х шамасының орта арифметикалық Мх –тен ауытқуы; у-У шамасының Му-тен ауытқуы; Σx*у-х және у ауытқуларының көбейтіндісінің алгебралық қосындысы; N-салыстырылатын алғашқы нәтижелер қосның іріктеу көлемі; σx -алғашқы нәтижелер у үшін орта квадраттық ауытқу.

Мысал. Х айнымалысы бұлшық еттерін босаңсыту нұсқауларымен берілген тізе шартының шамасын өлшеу нәтижелерімен көрсетілген, ал У айнымалысы – бұлшық еттерін қатайту нұсқауымен берілген. (10.5.кесте) Тізе шарттарының шамалары бір – біріне қатыссыз туралы гипотеза тексеріледі.

1.Мx = Σx /N және Mу = Σу /N формулалары бойынша орта арифметикалық мәндерді есептейміз (Мx= 7,5 Mу =8,0)

2. Мx және Mу-тен ауытқу шамаларын табамыз. (4,5 -графа)

3.Х және У –ді квадраттаймыз: Х және У

Сонымен: τ =Σx*у/Nσx*σу =102,0/10*3,53*3,79=0,76

4.Орта квадраттық ауытқудың есептейтін формула бойынша σx және σу табамыз.(σx=3,53, σу=3,79)

5.Әрбір ауытқулар қосындысының көбейтіндісін табамыз

6.Табылған мәліметтерді формулаға қоямыз. Біздің мысалдан алынған корреляция коэффициенті τxу тізе шартының 2 шамасын өзара қатысты екенін көрсетеді.

3.2.13.2 Сұрақ атауы 2 Анализ алгоритмі.

3.2.13.3 Сұрақ атауы 3 Әдістің шектеуліктері.

3. Реттік шамаларды салыстырғанды τ,Спирмен бойынша рангілік корреляция коэффицентін (p), интервалды шамаларды салыстырғанда пайдаланылады

Дәріс №13.Өзін-өзі тексеру сұрақтары

1. Психодиагностикалық зерттеудің бланктер толтыру арқылы жүргізілетін сынақтарына жататын тәсілдер ата.

2. Есте сақтауды зерттеу әдістемелері көрсет.

3. Психофизиологиялық зерттеудің хаттамасын деректі рәсімдеп, құжаттау барысында тұлғаның қандай сапа-қасиеттері көрсетілген.

3.2.14 Дәріс №14. Корреляциялық статистика. Спирменнің корреляциялық коэфициенті.

1.Критерийдің жалпы тағайындалуы.

2.Анализ алгоритмі.

3.Әдістің шектеуліктері

3.2.14.1 Критерийдің жалпы тағайындалуы.

1.Бүгінгі күні эксперименттік психология мен математикалық психологияның өзара байланысы өте тығыз екені белгілі. Зерттеу нәтижелерін математикалық тұрғыдан өңдеу өте күрделі творчестволық процесс және үнемі ізденуді талап етеді. Зерттеуден алынған материалдарды өңдеу, оның нақты анализін жасау, гипотезамен, белгілі ғылыми нәтижелермен салыстыру ғылыми жалпылаудың негізі болып табылады. Эксперименттік зерттеудің қорытынды сатысына негіз болатын өңдеу сатысы зерттеудің методологиялық принциптеріне сүйеніп, алынған нәтижелерді сапалы және сандық (статистикалық) өңдеу анализінен өткізеді. Психологияға математиканы ендіру, эксперименттік зерттеулер талабынан туындады. Математиканың абстракциялық қуаты психология ғылымын жетілдіріп, табиғи ғылымдарға жақындатуда. Психология ғылымындағы сапалы анализдеу жағдайлары тек психикалық процестерге ғана емес, онда қолданылатын математикалық аппаратты да қамтуы керек. Математикалық операциялардың сапалы анализдері эксперименттен алынған зерттеу нәтижелерін анализдеу мен өңдеудің басты шарты болып саналады. Психологияда зерттеулерді математикаландыру міндетін шешу барысында қолданбалы математиканың ерекше бөлімі ретінде психометрия алынады. Бұрынғы кеңестік психологияда ол математикалық психология деген атау алады. Өлшеу процесі барлық эмпирикалық ғылымның негізіне жатады. Психологиядағы қолданылатын өлшеу процедураларының өзіндік ерекшеліктері бар. Психологиялық өлшеулер зерттеуге қатысты қолданылатын өлшеу шкалаларының типтерінен тәуелді болып топтанады. Мұнда ескеретін мәселе мынада, психологияда қолданылатын шкалаларды бөлу формальды сипатқа ие емес, әрбір шкала математикалық аппараттың белгілі бір шегінде ғана қолданылады. Психологиялық өзгергіштік немесе психологиялық шкалалау дегеніміз – психикалық процестер мен күйлердің ерекшеліктерін өлшеу үшін қолданылатын процестер мен күйлердің ерекшеліктерін өлшеуде қолданылатын эксперименттік және математикалық тәсілдердің жиынтығы. С.С. Стивенстен кейін «шкалалау» терминінің орнына «өлшеу» ұғымы қолданылады. Психологиялық процестерді шкалалау дегеніміз оларға сандарды белгілі бір ережемен теңестіру.Ол сандар өлшеуге түсетін құбылыстарды бейнелейді. Эмпирикалық жүйелерді математикалық жүйелер көмегімен суреттеп, әректтерді сандар қатынасымен алмастыратын өлшеу психология ғылымын суреттеуші сипаттан жаңа фактілерді көрсете алатын ғылымдарға айналдырады. Психологиялық өлшеудің ерекшелігі мынада, сандар теңестірілетін обьектілер үшін психикалық құбылыстардың өздері алынбайды, мінез-құлық пен іс-әрекеттің әртүрлі «бірліктері» және физиологиялық реакциялар алынады. Зерттеу нәтижелерін анализдейтін сандық және сапалы сипаттамалар-көрсеткіштер деп аталады. Кез-келген әрекет көптеген факторлармен шарттанады. Олардың кейбіреулері лабораториялық экспериментте де бақылауға көнбейді. Сондықтанда психологияда қолданылатын көптеген көрсеткіштер кездейсоқ шамалар болып табылады, яғни ықтималдылықтар арқылы сандық мәндердің көптігі ретінде қолданылатын шамалар болып табылады. Ғылыми қорытындылар бір ғана мәліметпен шектелмейді, көп мәліметті кажет етеді, ондай көптіктерді алу үшін өлшеулерді көп рет қайталау керек. Одан алынған сансыз көп сандық мәндерді математикалық статистиканың көмегімен арнайы өңдеу керек. Сондықтанда психолог зерттеуші әртүрлі зерттеу мәліметтерін жинаумен қатар оларды өңдеудің математикалық тәсілдерін игеру керек. Мәселен зерттеуден алынған орташа мән өлшенген процестің шын шамасы деуге болмайды, алайда оны «қателер» немесе өлшеу методикасы дәл деп те түсінуге болмайды. Бұл шама ықтималды мән болып табылады. Ықтималдылық математикалық термин, бұл ұғым шектеулі ұғым, кездейсоқтық ұғымымен математикалық тұрғыдан тәуелді. Психикалық құбылысты өлшеуде оның статистикалық сипаты көрінеді. Психикалық процестердің өту шарты мен өту салдарының арасында біржақты немесе функционалды байланыс жоқ. Бұлар статистикалық жиынтықты немесе сапалы және сандық жиынтықты өзіне жинайды. Статистикалық заңдылықтарды бөлу немесе анализдеу және берілген құбылысты қажетті және кездейсоқ деп бөлу мәселелерімен математикалық статистика айналысады. Психологияда өлшенетін көрсеткіштердің «кездейсоқтығы» немесе «тербелісі» физикадағыдай емес басқаша мәнге ие. Психикалық процестері мәні жағынан өзгермелі және фактінің өзін тұрақты ету үшін сыртқы жағын қамтиды, ал оның ішкі шарттар жүйесі психикалық іс-әрекеттің өзін детерминациялайды, сондықтан да ол тұрақтанбайды. Математикалық статистика тәсілдерін қолдану өлшеудің және сыналушылардың белгілі бір санын талап етеді. Бұл талаптар немесе статистикалық жиынтықтардың репрезентативтілігі математикалық жоспарлау сатысына өтеді. Алайда математикалық статистика әдістері өлшенген белгілердің өзгерген мәндеріне бірдей қолданыла бермейді. Сондықтанда статистикалық бөлуі формаларының өзін анализдеу қажет. Осыған байланысты өңдеуге адекватты математикалық аппаратты дұрыс іздеу керек. Математикалық статистика көп жақты пән, оның ішінде біз көп өлшемді және факторлы анализ, ықтималдылықтар теориясы, аналитикалық геометрия және басқа да аспектілерін қарастырған жоқпыз. Бұл математикалық теорияларды оқып үйрену үшін алдымен қарапайым математикалық статистика негіздерін білу керек. Біз өзімізге мына міндеттерді жүктедік: студенттерде математикалық әдістерді психологиялық зерттеулерде қолдану негіздерін қалыптастыру; негізгі математикалық ұғымдарды психологиялық зерттеулерде қолдана алу білімдерін тереңдету; психологияда кеңінен қолданылатын эксперимент нәтижелерін талдау әдістері мен модельдеу тәсілдерін беру. Сонымен жалпы алғанда психологиядағы барлық сандық бағалау мәні бойынша статистикалы болып саналады. Алынған зерттеу нәтижелері математикалық статистика көмегімен өңделеді. Математикалық статистика математиканың қолданбалы саласының бірі, эмпирикалық мәліметтерді талдайды және жүйелендіреді. Статистика-бақылау тәсілі, оның әдісі, мәліметтерді жинау және оны талдау. Ең бастысы таңдалған методиканың валидтылығын, сенімділігін және обьективтілігін дәлелдеу. Алынған зерттеу нәтижелері белгілі бір стстистикалық көрсеткіштер арқылы суреттеледі.Соның негізінде оларға сәйкес математикалық тәсілдерді қолдануды үйрену әрбір зерттеушінің кәсіби міндеті болып табылады «Статистика» деген сөз жиі турде «математика» деген сөзбен, күрделі формулалармен ассоциацияланып студенттерді үркітіп жүреді. Статистика (Мак Коннелл) ол ең алдымен ойлау тәсілі, оны қолдану үшін математиканың тек негізін ғана білу жеткілікті. Күнделікті өмірде өзіміз байқамаймыз статистиканы күнде жасаймыз. Бюджетті жоспарлаймыз, үнемдейміз сонымен қатар алған имформацияларды таңдаймыз, топтаймыз, жіктейміз, реттейміз оларды басқа мәліметтермен байланыстырамыз соның арқасында дұрыс шешім алуға тырысамыз. Осы жағдайлар ғылыми мәліметтерді синтездеу операциясынан ешбір айырмасы жоқ болады. Осы жағдайдың бәрін толық түсіну үшін статистика туралы хабарымыз болуы керек. 1.Суреттеуші статистика - алынған мәліметтерді кестелейміз, графикке саламыз, нәтижелерді бөлу көрсеткіштерін кесте, график түрінде өрнектейміз, сол берілген бөлудің орташа мәндерін есептейміз, оның жайылуын (размах) және дисперсияны есептейміз. 2. Индуктивті статистика - сол популяциядан алынған таңдау (выборки) берген мәліметтерді барлық популяцияға тарата аламыз ба сол жағдайды тексеруден тұрады.

Дата добавления: 2014-12-25