Теорема сложения вероятностей

Суммой А+В двух событий А и В называется событие, состоящее в появлении события А или В, или обоих этих событий. Например, если из орудия произведены два выстрела, событие А - попадание при первом выстреле, событие В — попадание при втором выстреле, то событие А+В — попадание при первом выстреле, или при втором, или в обоих выстрелах.

В частности, если два события А и В — несовместимы, то А+В событие, состоящее в появлении одного из этих событий.

Рассмотрим более сложный случай. Пусть имеются три станка. Событие A ₁ — безотказная работа первого станка (событие 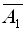—отказ в работе первого станка), событие А ₂ — безотказная работа второго станка (событие 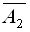—отказ в работе второго станка). Событие А ₃ — безотказная работа третьего станка. (Событие 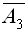—отказ в работе третьего станка).

Событие — безотказная работа только одного станка представляет собой сумму трех событий 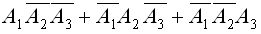, состоящее в безотказной работе первого станка и отказе в работе второго и третьего станков — событие 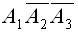; в безотказной работе второго станка и в отказе работы первого и третьего станков — событие ; в безотказной работе третьего станка и в отказе в работе первого и второго станков — событие 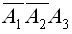. Итак, суммой трех указанных событий 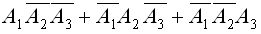называется событие, состоящее в появлени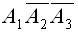и события или события илисобытия .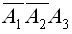

Как найти вероятность суммы случайных событий, если известны вероятности появления каждого из этих событий в отдельности?

Рассмотрим вначале несовместные события.

Теорема 1.

Вероятность суммы нескольких несовместных событий A₁, A₂...A_n равна сумме вероятностей этих событий

Р (А₁+А₂…+А_n) =Р (А₁) +Р (А₂) +...+Р (А_n).

Доказательство:

Проведем доказательство этой теоремы для схемы урн. Введем обозначения: n -общее число шаров в урне (цветных и белых), m - общее число цветных, (m ₁ — число шаров определенного цвета), так что .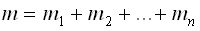

Число элементарных исходов, благоприятствующих извлечению цветного шара, равно 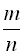. Следовательно

.

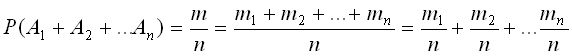Принимая во внимание, что ,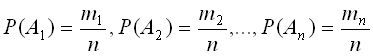

Окончательно получим .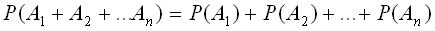

Теорема 2.

Сумма вероятности событий А₁, А₂...А_n, образующих полную группу, равна единице. Так как появление одного из событий полной группы достоверно, а вероятность достоверного событий равна единице, то

Р (А₁+А₂+...+А_n) = 1

События, составляющие полную группу событий, несовместны, поэтому, применяя теорему сложения вероятностей, получим:

Р (А ₁ +А₂+...+А_n) =Р (А ₁) +Р (А₂) +...+Р (А_n).

Окончательно

Р (А₁) +Р (А₂) +...+Р (А_n) = 1.

Противоположными называются два события, образующие полную группу событий. Из предыдущей теоремы следует, что сумма вероятностей противоположных событий А и 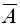равна единице.

Пример 1.5.1.

По цели осуществляется залп из двух орудий. Вероятность попадания в цель из первого орудия , из второго 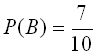. Какова вероятность поражения цели, если для этого достаточно хотя бы одного попадания в цель?

Исходим из того события: хотя бы одно попадание в цель и промах образуют полную группу событий. Искомая вероятность равна:

.

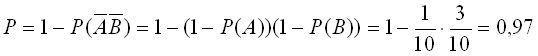Пример 1.5.2.

Вероятности обрывной работы трех ткацких станков равны, соответственно 0,1; 0,2 и 0,3. Найти вероятность безобрывной работы хотя бы одного из станков.

Решение:

События "работает безобрывно хотя бы один из станков" и "работают с обрывом все станки" составляют полную группу событий. Обозначим события - обрывную работу первого, второго и третьего станков соответственно через .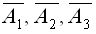

Искомая вероятность Р равна .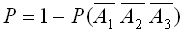

События 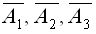—независимые. Применяя теорему умножения вероятностей, окончательно получим

Р =1- Р (А ₁) Р (А ₂) Р (А ₃)=1-0,1 0,2·0,3 = 0,994.

Пример 1.5.3.

Работница обслуживает три ткацких станка. Вероятность того, что в течение времени первый станок (событие A ₁ не потребует внимания Р (A ₁)=0,9, второй (событие А ₂) — Р (А ₂)=0,8 и третий (событие А ₃) Р (А ₃)=0,7. Найти вероятность того, что в течение того же времени:

а) все три потребуют внимания;

б) только один потребует внимания;

в) только два потребуют внимания.

а) События 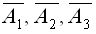противоположны событиям А ₁, А ₂, А₃ соответственно, следовательно:

; .

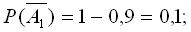
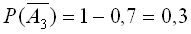Вероятность того, что все три машины потребуют внимания равно

;

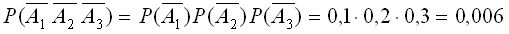б) Событие — работает только один станок, представляет собой сумму трех событий:

,

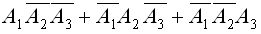Используя теорему сложения и умножения вероятностей, искомая вероятность равна:

.

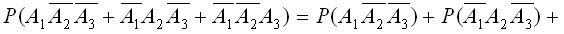
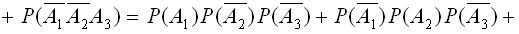
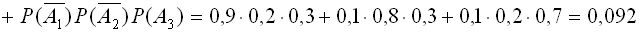в) Событие — работают только два станка, представляет собой сумму трех событий:

.

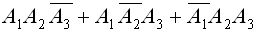Искомая вероятность равна:

.

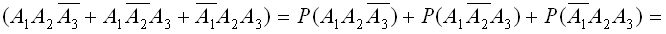
Рассмотрим теорему сложения вероятностей для совместных событий.

Теорема 3.

Вероятность суммы двух совместных событий A ₁ ,А₂-Р (A ₁ +A₂) равна сумме вероятностей этих событий Р (A ₁) и Р (А ₂) без вероятности их совместного появления P (A ₁ A ₂)

P (A _l+ A ₂) = P (A _I) + P (A ₂) - P (A₁A₂).

Доказательство:

Поскольку события A ₁ и А ₂ по условию совместны, то событие A ₁+ А ₂ наступит, если наступит одно из следующих несовместных событий:

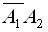, или .

По теореме сложения вероятностей,

Р (А₁+А₂) = 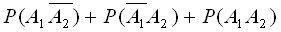(1).

Событие A ₁ наступит, если наступит одно из несовместных событий и .

По теореме сложения вероятностей

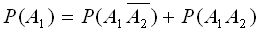, отсюда 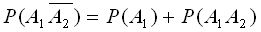(2)

Аналогично

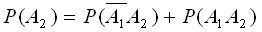, или .

Подставляя выражения (2) и (3)в выражение (1) получим:

.

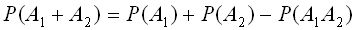На этом заканчивается доказательство теоремы.

Пример 1.5.4.

Вероятность попадания в цель при стрельбе из первого и второго орудий соответственно равна Р (А₁) = 0,7; Р (А₂)=0,8. Найти вероятность попадания при одном залпе (из обоих орудий), хотя бы одним из орудий.

Решение:

Искомая вероятность:

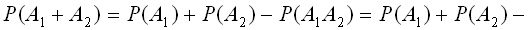
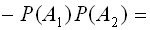0,7 +0,8 -0,56=0,94.

Дата добавления: 2014-12-25