
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вероятность отклонения относительной частоты от постоянной вероятности в независимых событиях
|
|
|
|
Пусть производится п, независимых повторных испытаний, в каждом из которых вероятность появления интересующего события равна Р. Найдем вероятность осуществления неравенства
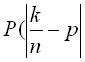 < δ)
< δ)
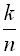 — относительная частота; δ >0 наперед заданное положительное число.
— относительная частота; δ >0 наперед заданное положительное число.
Неравенство  < δ перепишем в виде
< δ перепишем в виде  или после элементарных преобразований
или после элементарных преобразований
 .
.
Воспользуемся формулой предыдущего параграфа, обозначив
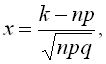
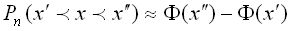
 .
.
При выводе последнего соотношения было учтено тождество
Ф(х)=-Ф(-х).
Пример 1.11.3.
Вероятность, что деталь нестандартна, р =0,1. Найти вероятность, что среди 900 деталей, относительная частота появления нестандартных деталей будет отличаться от постоянной вероятности р =0,1 по абсолютной величине менее; δ =0,03.
Решение:
Найдем искомую вероятность, пользуясь формулой
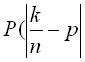 < δ)
< δ) 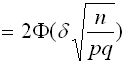 , получим
, получим
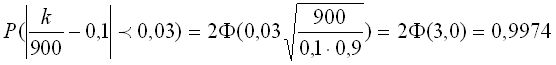 .
.
В группах по 900 отобранных деталей в 99,74% случаев отклонение относительной частоты появления нестандартной детали от вероятности Р =0,1 не превысит δ =0,03, т.е. не осуществится неравенство
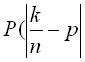 > δ).
> δ).
Пример 1.11.4.
Вероятность появления нестандартной детали р =0,1. Найдем, сколько надо отобрать деталей, чтобы с вероятностью, равной 0,9974, можно было утверждать, что относительная частота появления среди отобранных деталей нестандартных деталей будет отличаться от постоянной вероятности р =0,1 по абсолютной величине не более,чем на δ= 0.03.
Решение. Для решения воспользуемся формулой
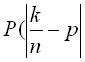 < δ)
< δ) 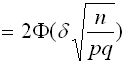 .
.
По условию p =0,1, q =0,9, δ =0,03

 .
.
По таблице для функций Фнаходим 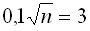 , следовательно n =900.
, следовательно n =900.
Полученный результат можно пояснить следующим образом. Если брать группы по 900 деталей, то в 99,74% случаев в указанной группе, будет нестандартных деталей не менее 63 (7% от 900), и не более 117 (13% от 900).
2. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
2.1. Определение дискретной случайной величины.
Определение:
Переменная величина х, принимающая в результате испытаний одно из конечной или бесконечной последовательности значений x 1, х 2,..., х n называется дискретной случайной величиной, если каждому значению х n соответствует определенная вероятность Рn того, что переменная величина х примет значение х n.
Закон распределения вероятностей дискретной случайной величины х можно представлять в виде таблицы:
Пример 2.1.1. Переменная величина х есть число очков, выпадающих на верхней грани игральной кости при ее однократном бросании. X в этом случае принимает одно из следующих значений: 1,2,3,4,5,6. Вероятность выпадания каждого значения есть
То, что случайная величина х примет одно из значений последовательности x 1, х 2,..., х n, есть событие достоверное и поэтому выполняется условие:
Пример 2.1.2. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 рублей и десять выигрышей по I руб. Найти закон распределения случайной величины х -стоимости возможного выигрыша для владельца одного лотерейного билета. Решение: напишем возможные значения х: х 1=50, х2 =1, х 3=0. Вероятности этих возможных значений Р 1=0,01; Р 2=0,1; Закон распределения запишем в виде
|
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 603; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 . Следовательно, закон распределения этой случайной величины будет иметь вид:
. Следовательно, закон распределения этой случайной величины будет иметь вид: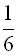
 в случае конечной последовательности или
в случае конечной последовательности или в случае бесконечной последовательности.
в случае бесконечной последовательности. .
.