Инженерная графика

Лист4

Лист 3

Лист2

Алгоритм решения задачи следующий (рисунок. 3):

1. Определяем натуральную величину плоскости S(A, EF) и строим основание тетраэдра. Для этого используем способ замены плоскостей проекций. Заменим плоскость П₂на плоскость П₄(П₅^π 1 Ù П₄çç S(AEF), при этом ось x14 ⊥ h1, а затем П₁заменяем на П₅(П₅^ П₄Ù П₅|| S(A, EF)), при этом ось x45 || Sπ 4. После этого строим основание тетраэдра – равносторонний треугольник A5B5C5. Для нахождения новых проекций точек проводим новые линии связи перпендикулярно к новым осям. На их продолжении от новых осей откладываем отрезки, равные расстояниям от заменяемых проекций точек до предыдущих осей. Конечная точка отрезка является искомой проекцией точки на новой плоскости проекций.

Например: | x14A4 | = | x12A2 |; | x45A5 | = | x14A1 |.

2. Строим плоскость медиального сечения Q, и находим проекцию вершины тетраэдра точку S5. Затем произведем еще одну замену плоскостей проекций. Плоскость П₄заменим на плоскость П₆(П₆^ П₅Ù || Q). В новой плоскости строим проекции основания тетраэдра и его вершины S6. Для чего из точки B6 на линии связи S5S6 делаем засечку радиусом, равным натуральной величине ребра тетраэдра. Найдя проекции точек всех вершин тетраэдра в плоскостях проекций П₅и П₆, обратными построениями находим проекции этих точек в исходных плоскостях П₁и П₂. Выполнив все построения, необходимо выделить цветными карандашами

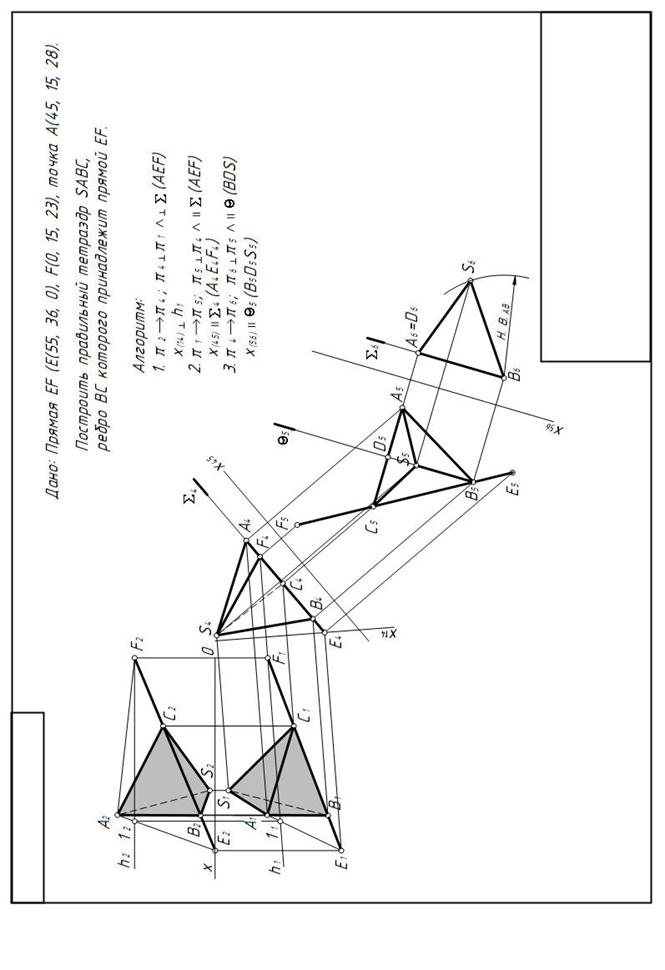
Рисунок 3 Построение тетраэдра

проекции тетраэдра с учетом видимости его ребер. Видимость определяется методом конкурирующих точек (в примере эти точки не показаны).

Для определения натуральной величины грани SAC надо преобразовать чертеж так, чтобы плоскость грани стала параллельна плоскости проекций.(рисунок 4) Для этого сделаем две замены плоскостей проекций: сначала заменим плоскости проекций так, чтобы плоскость грани стала перпендикулярной плоскости П₄, а затем параллельной плоскости П₅.

Проведем в треугольнике SAC горизонталь h и расположим П₄перпендикулярно горизонтали (Х _1,4^ h1) (см. рисунок. 3). Для нахождения новых проекций точек проводим линии связи перпендикулярно к новым осям. На их продолжении от новых осей откладываем отрезки, равные расстояниям от заменяемых проекций точек до предыдущих осей (на рис. 4 они помечены черточками). В результате первой замены плоскостей проекций плоскость треугольника SAC станет перпендикулярной к плоскости П_4. Треугольник спроецируется в отрезок S4A4. Затем делаем вторую замену плоскостей проекций (плоскость П₅параллельна плоскости треугольника (ось x45 || S4A4)), на плоскости П₅получим натуральную величину треугольника S5A5C5 = SAC.

Двугранный угол спроецируется в линейный, если общее ребро угла станет перпендикулярным к плоскости проекций. Сначала поворачиваем двугранный угол так, чтобы общее ребро стало параллельным плоскости проекций и перемещаем в параллельных плоскостях на свободное место, а затем поворачиваем двугранный угол до положения перпендикулярного к плоскости проекций и перемещаем еще раз в параллельных плоскостях на свободное место.

Перемещаем двугранный угол в свободное поле чертежа без изменения горизонтальной проекции (см. рисунок. 5). Проекции ребра A'1С'1 = A1C1 ставим параллельно оси x, и затем методом засечек определяем положение проекций точек B'1, S' 1. (Расстояния A' 1 B'1 = A1B1, С'1B'1 = C1B1 и A'1S'1 = A1S1, С'1S'1 = C1S1). Затем определяем фронтальные проекции точек A'2, B'2, С' 2, S' 2. Проводим вертикальную линию связи из проекции точки A' 1 и фронтальный след горизонтальной плоскости, в котором перемещается точка, и на пересечении получим проекцию A'2. Аналогично определяем проекции B'2, C'2, S'2. Затем перемещаем двугранный угол в свободное поле чертежа до положения перпендикулярного к П₁. Проекции ребра A'' 2 С'' 2 = A'2C'2 ставим перпендикулярно оси x, и затем методом засечек определяем положение проекций точек B''2, S''2. (Расстояния A''2B''2 = A'2B'2, С''2B''2 = C'2B'2 и A'' 2 S'' 2 = A'2S' 2, С''2S''2 = C'2S'2). И, наконец, определяем горизонтальные проекции точек A''1 = С''1, B''1,, S''1). Проводим вертикальные линии связи из проекции точки A''2 и горизонтальные следы фронтальных плоскостей, в которых перемещается точка A из A'1, и на пересечении получим проекцию A''1. Аналогично определяем проекции B''1, C''1, S''1. и, таким образом, получаем искомый угол α.

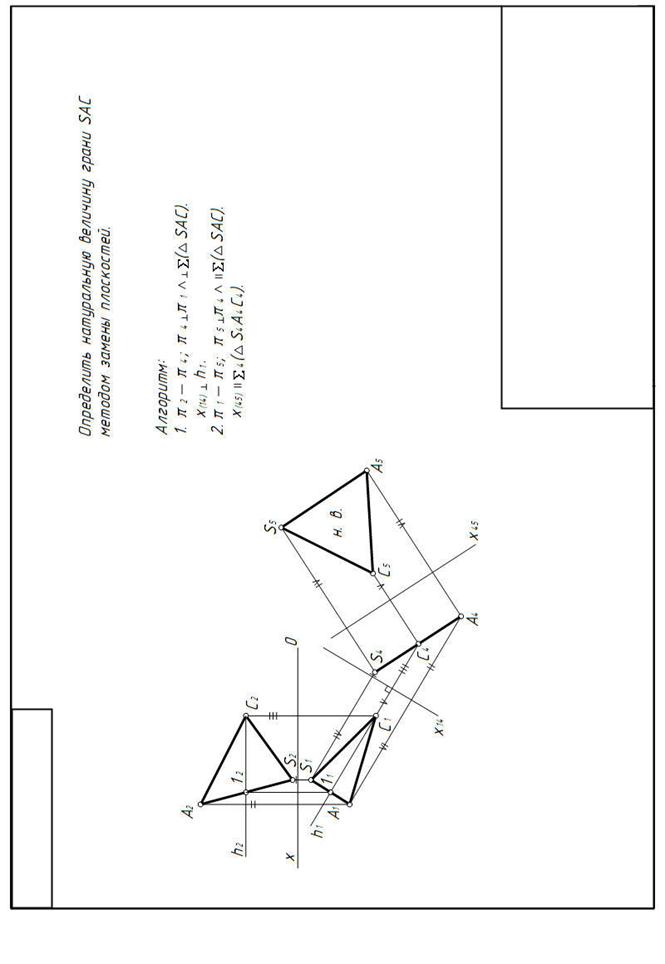
Рисунок 4 Определение натуральной величины грани

Примечание. В вариантах 6 и 16 построения необходимо выполнять используя метод вращения. На рисункеt 5 показано построение прямой SC, наклоненной под углом 30° к плоскости П₂и 45° к плоскости П₁.

1. Для построения выбираем произвольную точку S (S1, S2) и проводим две прямые линии: SA || П₁ (S1A1 || x12) и наклоненную к плоскости П₂ под углом 30° и SB || П₂(S1B1 || x12) и наклоненную к плоскости П₁под углом 45°. При этом | SA | = | SB |.

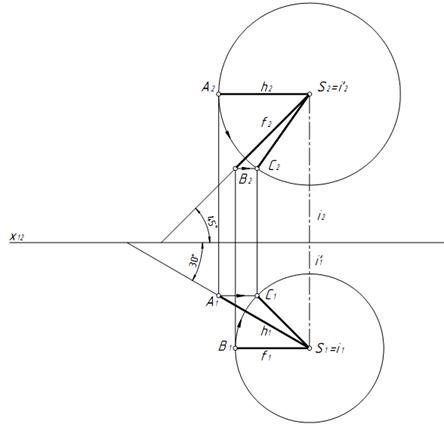
Рисунок 5 Метод вращения вокруг оси i

2. Вращаем отрезок SB вокруг оси i перпендикулярной П₁, а отрезок SA вокруг оси i' перпендикулярной П₂до совмещения этих отрезков.

3. Совместившиеся отрезки будут принадлежать прямой SC, наклоненной к плоскости П₁под углом 45° и к плоскости П₂под углом 30°.

Задача3. Лист 5

Даны ортогональные проекции двух поверхностей.

Требуется построить линию пересечения поверхностей в ортогональных проекциях. Построить развертки двух поверхностей с нанесением линий пересечения.

Эпюр выполняется на трех листах чертежной бумаги формата А3 в масштабе 1:1. Задание представлено в табл. 2. На первом листе необходимо определить линии пересечения этих поверхностей. Задачи рекомендуется решать способами секущих плоскостей и концентрических сфер (рисунок 6).

Рассмотрим решение первой части эпюра.

Т а б л и ц а 2 З а д а н и е к задаче № 3

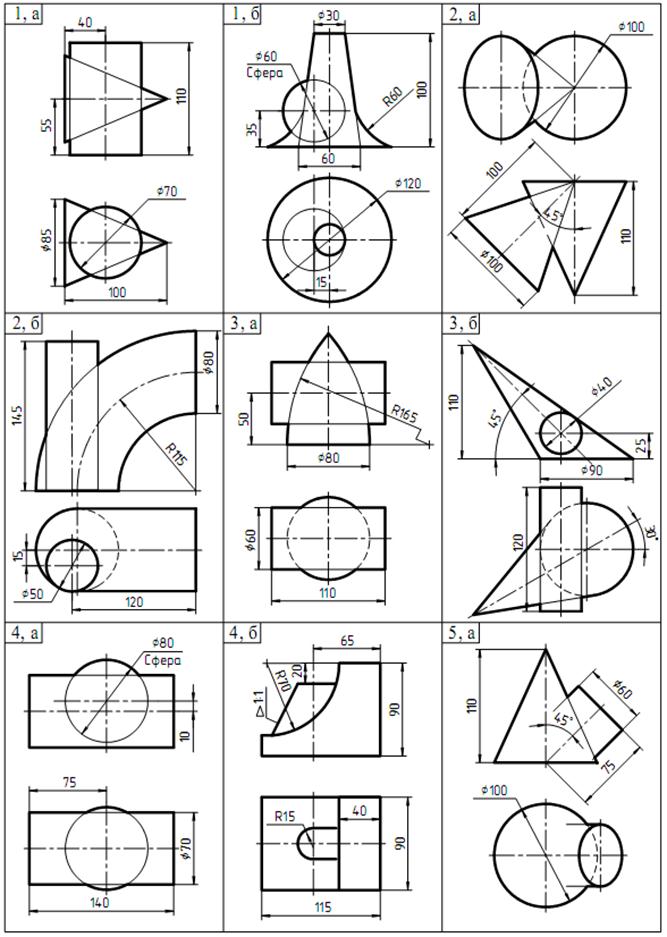
Продолжение таблицы 2

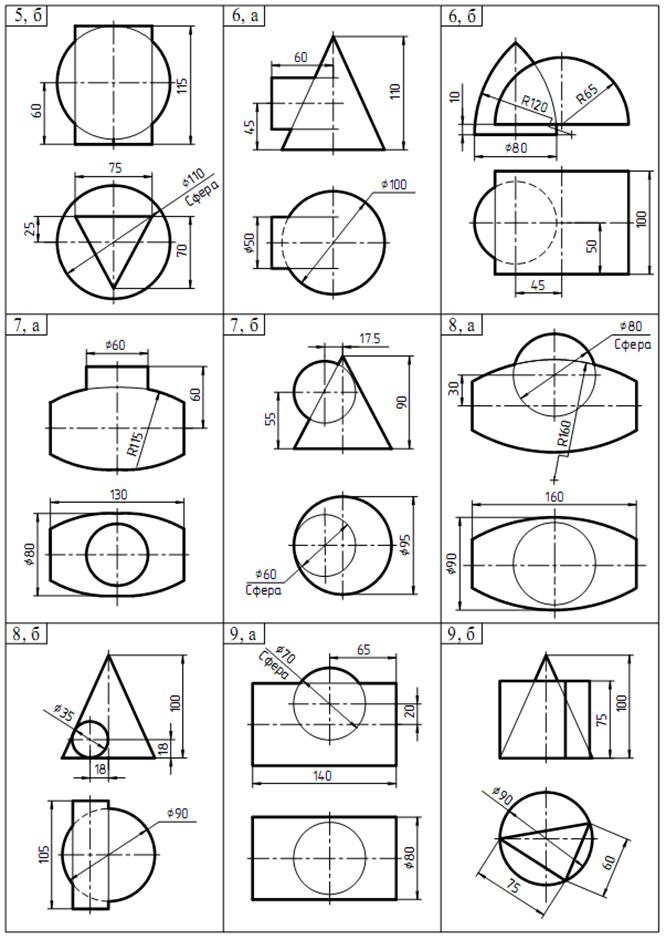
Продолжение таблицы 2

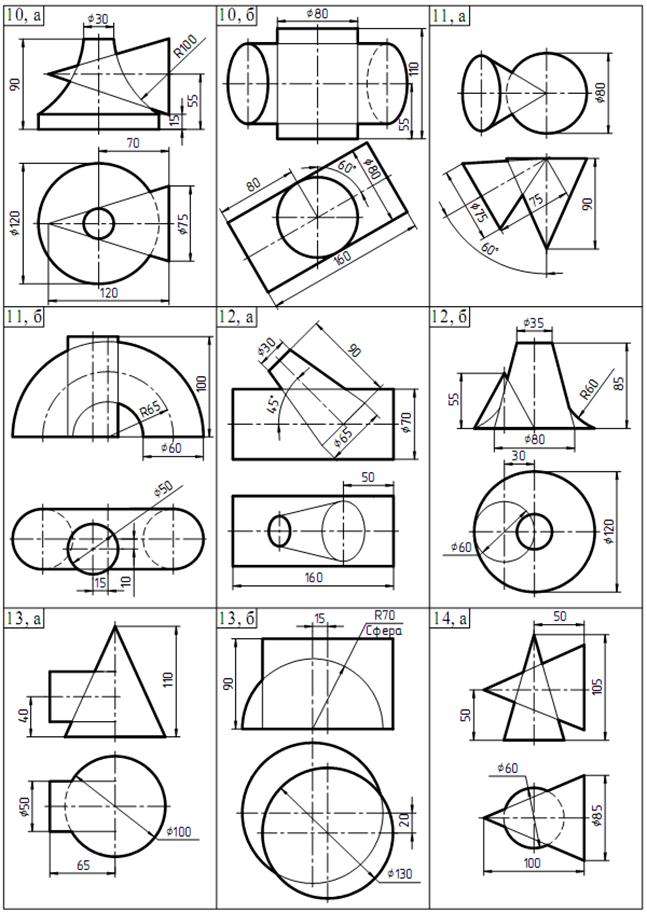
Продолжение таблицы 2

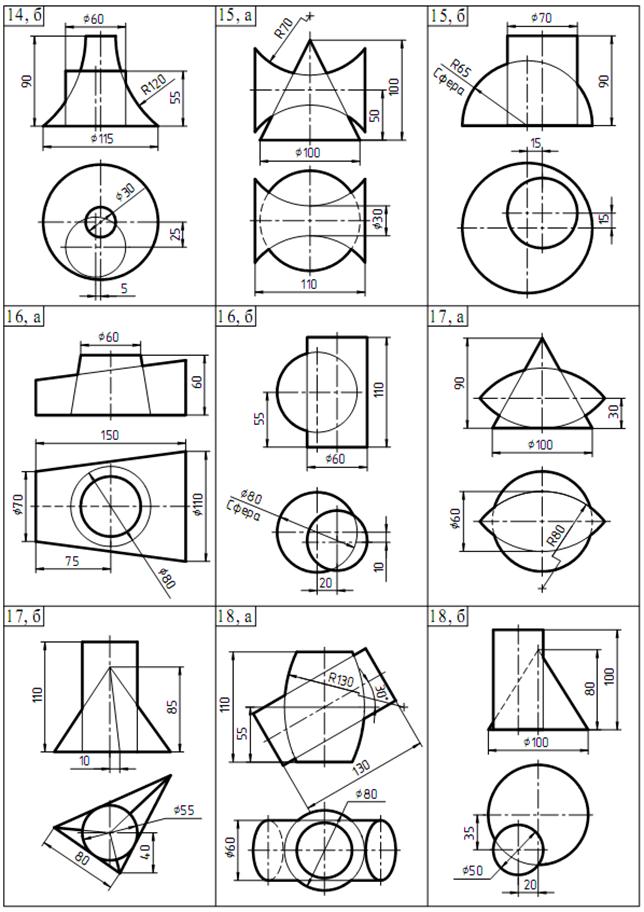
Продолжение таблицы 2

Продолжение таблицы 2

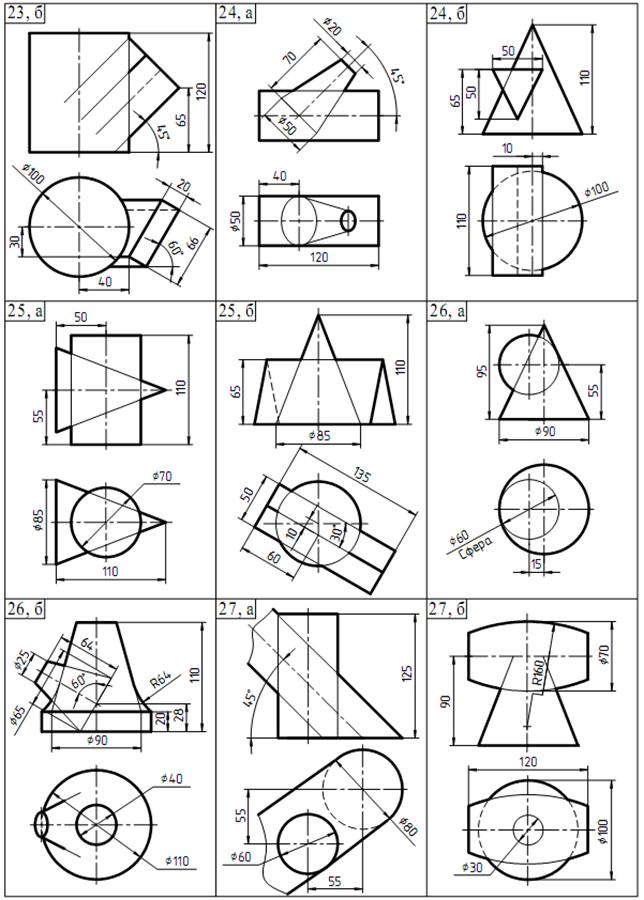
Перечертить на первый лист из таблицы 2 пересекающиеся поверхности размеры не проставлять Для нахождения линий пересечения двух поверхностей выбираем рациональный способ решения, т. е. выбираем такие секущие плоскости или сферы, которые бы одновременно пересекали обе заданные поверхности по прямым линиям или окружностям). Каким бы способом не решалась задача, построение линии пересечения надо начинать с определения опорных точек. К этим точкам относятся:

– точки, проекции которых лежат на проекциях очерковых линий одной из поверхностей, например на крайних образующих цилиндра или конуса, на главном меридиане и экваторе сферы, а также точки, отделяющие видимую часть линии пересечения от невидимой;

– точки, наиболее удаленные от плоскостей проекций и наиболее близкие, высшие и низшие.

Этапы решения задачи пересечения сферы с конусом (см. рисунок 6):

1. Решение начинаем с построения опорных точек A и B. Через ось симметрии проводим плоскость λ || π 2, которая пересекает поверхности сферы и конуса по очеркам на фронтальной плоскости проекций. По линиям связи находим горизонтальные проекции точек A (A1) и B (B1).

2. Находим точки 1 и 2, которые отделяют видимую часть линии пересечения от невидимой. Для этого через экватор сферы проводим секущую плоскость S || π 1 ^ ^П₂(S 2), которая пересечет сферу по окружности радиуса R, а конус – по окружности радиуса r. В пересечении этих окружностей на плоскости П₁определятся точки 11 и 21, а по линиям связи – 12 и 22.

3. С помощью горизонтальных плоскостей-посредников β и γ, которые пересекают данные поверхности по окружностям находим точки 3, 4, 5, 6

4. Фронтальную и горизонтальную проекции линии пересечения сферы с конусом обводим красным цветом (с учетом видимости).

Во второй задаче даны конус и наклонный цилиндр, оси которых пересекаются и лежат в одной плоскости, параллельной плоскости π 2. Поэтому для построения линий пересечения принимаем способ концентрических сфер, центр которых расположен в точке O пересечения осей.

1. Решение начинаем с определения проекций A2, B2, A1, B1 опорных точек A и B, лежащих на пересечении очерковых образующих поверхностей.

2. Чтобы определить точку перегиба линии пересечения, необходимо задать сферу Rmin. Ее выбираем так, чтобы она вписалась в очерк одной поверхности и пересекала очерк другой поверхности. В данном случае сфера Rmin касается образующих конуса и пересекает образующие цилиндра. На основании теории о соосных поверхностях заданные поверхности будут пересекаться со сферой по окружностям, которые на π 2 проецируются в отрезки прямых. В пересечении этих отрезков отмечаем общие точки 12 и 12, принадлежащие обеим заданным поверхностям. По линии связи находим горизонтальные проекции 11 и 21.

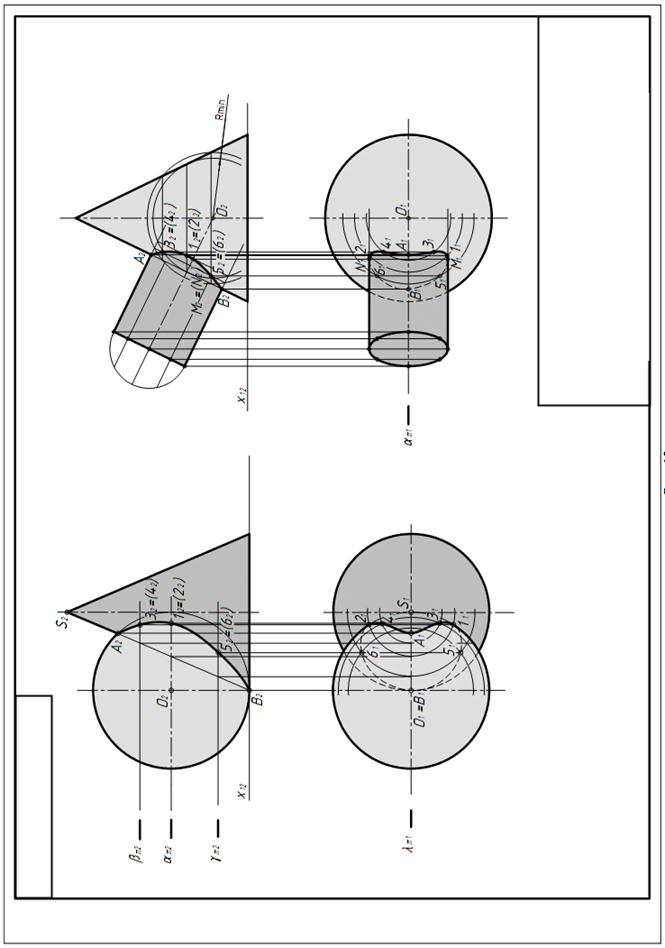
Рисунок 6, Построение линии пересечения поверхностей

3. Изменив радиус вспомогательной сферы на больший, чем Rmin, но оставив ее центр в точке O (O2), определяем промежуточные точки линии пересечения заданных поверхностей (52 = 62; 32 = 42). По линиям связи находим их горизонтальные проекции.

4. Там, где линия пересечения на π 2 пересекает ось цилиндра, отмечаем точки M (M2) = N (N2), отделяющие на π 1 видимую часть линии пересечения от невидимой на горизонтальной плоскости проекций.

5. Обводим линию пересечения красным цветом (с учетом видимости)

Рассмотрим решение второй части задачи. Построение развертки двух из четырех поверхностей с нанесением линии пересечения. Разверткой поверхности называется фигура, построенная совмещением ее с плоскостью. Развертка цилиндрической поверхности выполняется аналогично развертке призмы.(рисунок 7)

Развертка конической поверхности выполняется аналогично развертке пирамиды. Сначала в заданный конус вписываем n-угольную пирамиду, затем строим развертку боковой поверхности вписанной пирамиды. Соединив концы ребер плавной кривой, получаем приближенную развертку боковой поверхности конуса. Для нанесения линии пересечения на развертку конуса точки, принадлежащей линии пересечения, сначала проецируем на очерковую образующую, так как только она проецируется на плоскость П₂в натуральную величину. Затем замеряем расстояния L1 – L, отмечаем их на соответствующих образующих (см. рисунок 7, а, б), и соединяем полученные точки.

Для поверхностей, относящихся к неразвертываемым, например, сферы, тора, возможно построение условной приближенной развертки. Для выполнения ее поверхность обычно разбивают на ряд элементов, которые могут быть заменены элементами цилиндрической или конической поверхностей.

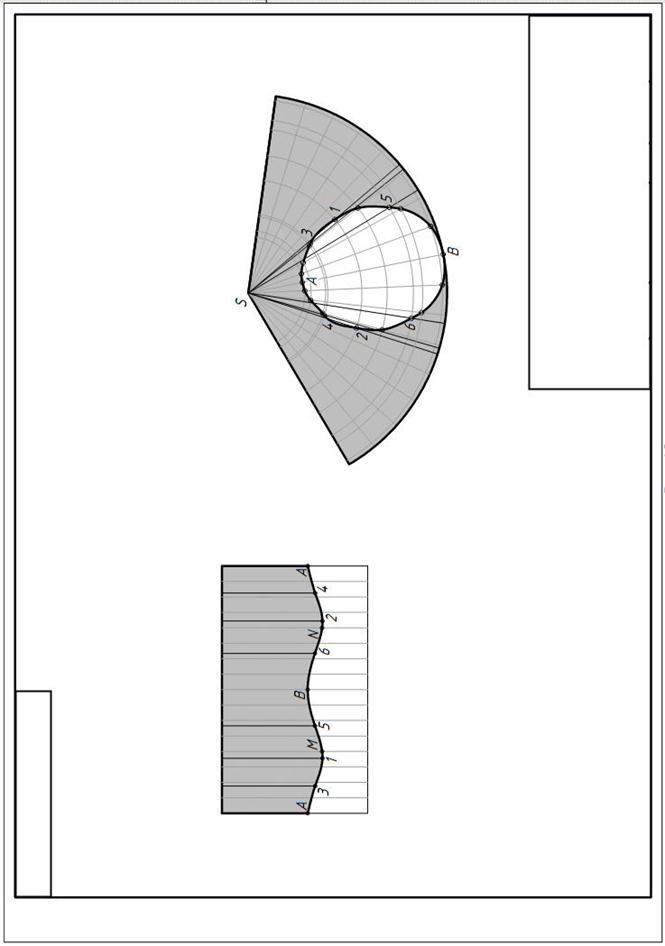
Рисунок 7 Построение развертки цилиндра и конуса

Лист1 (Титульный лист)

Работа является общей для всех студентов и выполняется с образца, помещенного на рисунке 8.

Целью выполнения чертежа является приобретение навыков в написании букв и цифр чертежным шрифтом в соответствии с требованием ГОСТа 2.304-81. Перед выполнением чертежа необходимо изучить ГОСТ 2.301-68, 2.304-81 и литературу.

На листе ватмана формата А4 вычертить рамку. Равномерно распределить содержание надписей на подготовленном формате, чтобы общий примерный центр тяжести надписей находился в центре листа. При выполнении надписей крупного размера необходимо подготовить сетку, состоящую из горизонтальных линий с расстоянием между ними, равными высоте букв соответствующего номера шрифта, и линий под углом 75о к основанию строки и расположенных друг от друга на расстоянии, равном ширине букв и промежуткам между ними.

Для мелких шрифтов (2,5; 3,5; 5) достаточно провести две горизонтальные параллельные линии. Для контроля правильности наклона букв проводят линии под углом 75о через 10-20 мм.

Сетку лучше проводить иглой по линейке или тонко заточенным карандашом Т или 2Т. Надписи выполнять шрифтом типа Б. Карандашом ТМ или М обвести буквы и цифры толщиной в соответствии с ГОСТ 2.304-81.

Рамку обвести карандашом толщиной не менее 0,7 мм.

Дата добавления: 2014-12-25