Робота сили ваги 4 страница

; ,

звідки

.

Підставивши значення сталих інтегрувань, дістанемо рівняння відносного руху кільця:

.

Підставляючи в ліву частину рівняння, визначимо значення 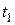тривалості руху кільця вздовж стержня:

,

звідки

.

Припустимо, що , а . Тоді останнє рівняння набуває вигляду:

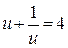або ,

звідки

.

Оскільки час руху кільця 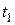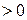, то . Тому з двох коренів обираємо 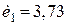, а не , що <1.

Таким чином, , звідки після логарифмування одержимо:

.

Для того щоб отримати модулі вертикальної і горизонтальної складових повної реакції стержня 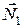та 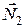спроектуємо векторне рівняння на осі 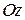та .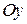

Враховуючи, що та 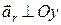, отримаємо відповідно:

та ,

звідки матимемо:

;

.

Таким чином, горизонтальна складова тиску кільця на стержень у поперечному напрямі, змінна за часом.

Розділ ХІІ Загальні теореми динаміки точки і механічної системи

Лекція 24

Загальні відомості про механічну систему.

МОМЕНТИ ІНЕРЦІЇ ТІЛ

24.1. Класифікація і властивості сил, що діють на механічну систему

Механічною системою матеріальних точок називається така їх сукупність, у якій положення або рух кожної матеріальної точки залежить від положення і руху всіх інших точок системи.

Якщо на рух матеріальних точок механічної системи не накладено жодних кінематичних обмежень, то така система називається вільною (Сонячна система).

Якщо вільність руху матеріальних точок механічної системи обмежується будь-якими в’язями, то така система називається невільною (будь-який механізм).

Введений розподіл механічних систем на вільні та невільні зумовлює розподіл сил, які діють на точки механічної системи, на задані та реакції в’язей, а також на зовнішні й внутрішні.

Зовнішніми називаються сили, з якими на точки заданої системи діють інші тіла, які не входять до складу цієї системи.

Внутрішніми називаються сили взаємодії між матеріальними точками однієї механічної системи.

В подальшому зовнішні сили будемо позначати 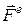, а внутрішні – .

Наведений розподіл сил на задані та реакції в’язей, а також на зовнішні й внутрішні є умовним. Одну й ту саму силу можна вважати як внутрішньою так і зовнішньою залежно від того, чи розглядаємо ми рух механічної системи в цілому або окремої її частини.

Внутрішні сили механічної системи мають такі властивості:

1. Головний вектор всіх внутрішніх сил механічної системи дорівнює нулю:

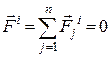. (24.1)

2. Головний вектор-момент всіх внутрішніх сил механічної системи відносно довільного нерухомого центра дорівнює нулю:

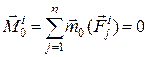. (24.2)

24.2. Центр мас механічної системи і його положення.

Маса системи дорівнює сумі мас її матеріальних точок:

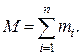
Рух механічної системи залежить не лише від маси системи і прикладених до її точок сил, а й від розподілу мас у цій системі.

Розподіл мас у механічній системі при її поступальному русі повністю характеризується положенням центра мас.

У розділі «Статика» виведені формули для визначення положення центра ваги тіла, яке характеризує розподіл сил ваги окремих частин тіла.

Якщо врахувати, що сили ваги пропорційні їх масі, то положення центра мас механічної системи можна знайти за формулою, аналогічною формулі для визначення центра ваги, тобто

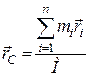. (24.3)

Якщо спроектуємо обидві частини векторного рівняння (24.3) на осі декартової системи координат, то отримаємо формули координат центра мас системи:

, , . (24.4)

Отже, центром мас механічної системи називається геометрична точка С, положення якої визначається з рівностей (24.3) або (24.4).

Неважко переконатись, що центр мас механічної системи збігається з положенням центра ваги тіла, яке знаходиться в однорідному полі тяжіння. Проте ці поняття не є тотожними. Поняття «центр мас механічної системи» зберігає свій зміст незалежно від того, знаходиться дана механічна система в однорідному полі тяжіння чи ні.

24.3. Момент інерції твердого тіла, що обертається навколо нерухомої осі. Радіус інерції.

Якщо тіло здійснює не поступальний рух, тоді для характеристики розподілу мас тіла відомості тільки про положення центра мас недостатньо.

Наприклад, якщо збільшити відстань від осі 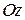кожної з кульок (рис. 24.1) на одну й ту саму величину, то при цьому положення центра мас не зміниться, але розподіл мас стане іншим.

Це зумовить інший характер обертання стержня АВ навколо осі Оz. Обертання стане більш сповільненим.

Врахувати такий розподіл мас дозволяює осьовий моменти інерції тіл.

Осьовий момент інерції тіла – це фізична величина, що характеризує міру інертності тіла під час його обертального руху навколо нерухомої осі.

Моментом інерції твердого тіла відносно деякої осі називається скалярна величина, яка дорівнює сумі добутків маси кожної з точок тіла на квадрат відстані від точки до даної осі (рис. 24.2):

; . (24.5)

При неперервному розподілі мас суми у формулах (24.5) переходять в інтеграли по всій масі тіла:

; ;

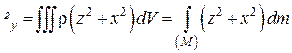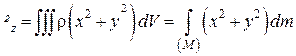. (24.6)

Тут 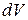– елементарний об’єм, координати якого x, y, z і маса ; 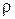– густина матеріалу об’єму.

Іноді зручно виразити момент інерції тіла відносно осі за допомогою радіуса інерції.

Радіусом інерції тіла називається відстань від осі до деякої уявної точки, в якій необхідно зосередити масу даного тіла, щоб момент інерції цієї точки відносно заданої осі дорівнював моменту інерції тіла відносно тієї самої осі:

, (24.7)

де – маса тіла; – радіус інерції тіла відносно осі Ох:

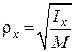. (24.8)

24.4. Теорема про моменти інерції тіла відносно паралельних осей:

Момент інерції тіла відносно довільної осі дорівнює моменту інерції відносно осі, яка паралельна їй і проходить через центр мас тіла, плюс добуток маси тіла на квадрат відстані між осями ().

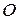Доведення. Центр мас тіла обираємо за початок відліку системи координат (рис. 24.3). Візьмемо на осі довільну точку за початок нової системи координат , осі якої паралельні до осей вибраної системи відліку . При цьому осі і 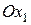збігаються.

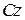Позначимо через відстань між осями і .

Визначимо моменти інерції даного тіла відносно осей 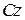і :

,

.

Встановимо залежність між координатами 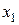і ; і . З рис.24.3 видно, що = , звідки .

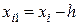Тоді .

Крім того .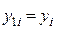

Підставивши ці значення в вираз для , отримаємо:

.

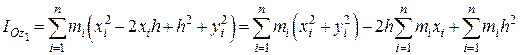Тут перший доданок – момент інерції тіла відносно осі 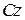. Третій доданок дорівнює добутку маси тіла на квадрат відстані між осями 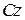і 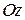, тобто

.

Для визначення другого доданку скористаємось першою з формул координати центра мас системи (22.4). Звідки

.

Тоді

,

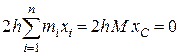оскільки 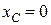за вибором системи відліку.

Остаточно маємо

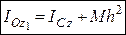. (24.9)

Теорему доведено.

24.5. Приклади визначення моментів інерції тіл канонічної форми

1. Моменти інерції тонкого однорідного стержня.

Визначимо моменти інерції однорідного стержня 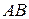масою і довжиною 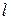відносно осі 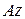, перпендикулярної до стержня. Вісь спрямуємо уздовж стержня 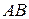(рис.24.4).

Рис.1

Виділимо елементарну ділянку стержня довжиною , яка знаходиться на відстані 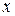від точки .

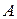Маса цієї ділянки стержня на початку відліку

де – густина матеріалу, S – площа поперечного перерізу стержня.

Тоді момент інерції стержня відносно осі 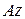дорівнює:

.

Оскільки маса всього стержня

,

то

. (24.10)

Для визначення моменту інерції стержня відносно осі , яка проходить через центр мас стержня, скористаємось теоремою про моменти інерції тіла відносно паралельних осей:

,

звідки

,

тобто

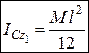. (24.11)

2. Моменти інерції однорідного кільця або порожнистого циліндра.

Кільце радіуса 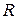має площу поперечного перерізу і густину матеріалу . Тоді маса кільця дорівнює:

.

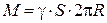Спрямуємо вісь 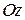перпендикулярно до площини рисунка та визначимо відносно неї момент інерції кільця (рис. 24.5).

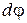Якщо виділити елементарну ділянку кільця довжиною з центральним кутом , то маса цієї ділянки кільця дорівнює:

Тоді для моменту інерції кільця відносно осі 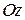маємо:

,

або . (24.12)

3. Момент інерції кругової однорідної пластини, диска або циліндра.

Розглянемо однорідну кругову пластину (рис. 24.6) радіуса 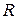і масою

,

де – густина матеріалу, h – товщина пластини

Виділимо елементарне кільце радіусами 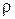і . Маса цього кільця дорівнює:

.

Момент інерції цієї пластини відносно центральної осі Оz, яка перпендикулярна до пластини, становить:

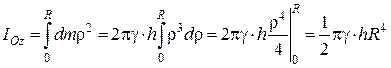
або

.

Отже,

. (24.13)

4. Момент інерції.кулі

Маса кулі

Виділимо в кулі елементарну пластину товщиною і радіуса 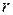, яка знаходиться від площини 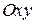на відстані (рис. 24.7). Елементарна маса цієї пластини

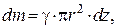
де r – радіус за теоремою Піфагора дорівнює

.

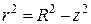Визначимо момент інерції такої елементарної пластини відносно осі 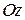за формулою (24.20):

.

Момент інерції кулі відносно осі 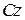дорівнює:

.

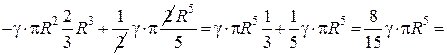
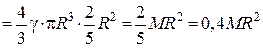Остаточно маємо:

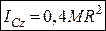. (24.14)

5. Момент інерції однорідного прямого колового конуса.

Маса прямого конуса

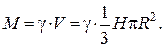
Виділимо в конусі пластину товщиною і радіуса 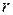, яка знаходиться від площини основи на відстані (рис. 24.8). Елементарна маса цієї пластини

,

де r – радіус, який визначається з такого співвідношення:

Визначимо момент інерції елементарної пластини відносно осі :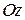

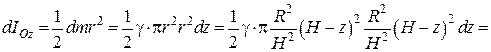
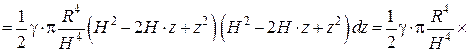
Момент інерції конуса відносно осі :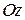

.

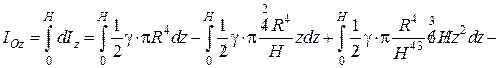
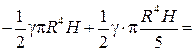
Під час перетворень взаємознищується відповідно перший та четвертий а також другий і третій доданки. Залишається тільки п’ятий.

Отже,

. (24.15)

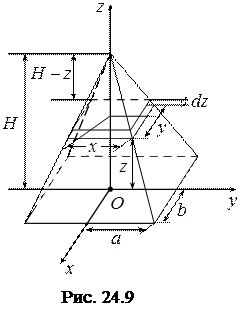
6. Момент інерції однорідної правильної прямокутної піраміди.

Для прямокутної піраміди (рис. 22.9) об’єм та маса визначаються за формулами:

; ,

де

; .

Виділимо в піраміді елементарну прямокутну пластину товщиною і сторонами та . Елементарна маса цієї пластини:

,

де 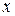та визначаються зі співвідношень:

, ;

, .^.

Тоді елементарна маса пластини:

.

Для моменту інерції відносно осі 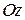матимемо:

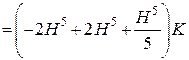
або

.

Отже, момент інерції прямокутної піраміди відносно її висоти дорівнює:

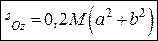. (24.16)

6. Моменти інерції прямокутного паралелепіпеда:

; ; . (24.17)

Лекція 25

РУХ ЦЕНТРУ МАС МЕХАНІЧНОЇ СИСТЕМИ. КІЛЬКІСТЬ РУХУ МАТЕРІАЛЬНОЇ ТОЧКИ. ГОЛОВНИЙ ВЕКТОР КІЛЬКОСТІ РУХУ МЕХАНІЧНОЇ СИСТЕМИ

25.1. Теорема про рух центра мас механічної системи

Центр мас механічної системи рухається як матеріальна точка, маса якої дорівнює масі механічної системи, під дією зовнішніх сил, прикладених до точок цієї системи.

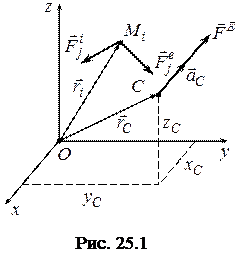Доведення: Нехай механічна система матеріальних точок рухається під дією зовнішніх () і внутрішніх () сил відносно обраної системи координат (рис. 25.1).

Положення центра мас 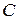системи визначається за формулою:

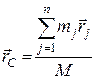, де . (25.1)

Запишемо диференціальні рівняння руху усіх 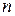точок механічної системи

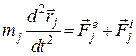
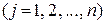. (25.2)

Підсумовуючи рівняння (23.2) за кількістю точок, дістаємо

. (25.3)

Перетворимо ліву частину рівняння (23.3), з урахуванням формули (25.1):

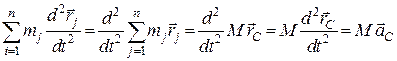. (25.4)

Враховуючи властивості внутрішніх сил механічної системи (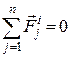) та підставляючи значення (23.4) в (23.3), остаточно дістанемо

Дата добавления: 2014-12-25