Робота сили ваги 6 страница

Позначимо елементарну площу трикутника 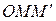через 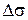, тоді

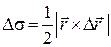, (26.11)

де 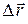– векторелементарного переміщення.

Розділимо обидві частини рівняння (26.11) на 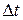і переходячи до границі при 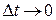, отримаємо

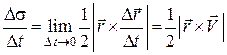. (26.12)

З урахуванням (26.10) маємо:

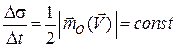. (26.13)

Величина 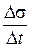називається секторною швидкістю і характеризує міру зміни у часі площі 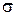, що описує радіус-вектор 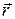точки .

Таким чином, я кщоточка рухається під дією центральної сили, то траєкторією її руху буде плоска крива і рухається вона із векторною сталою секторною швидкістю, тобто так, що її радіус-вектор за рівні проміжки часу описує рівні площі.

Це положення називається законом площ і являє собою другий закон Кеплера, щодо руху планет навколо Сонця.

Лекція 27

КІНЕТИЧНИЙ МОМЕНТ МЕХАНІЧНОЇ СИСТЕМИ

27.1 Головний момент кількості руху механічної системи або кінетичний момент механічної системи відносно центра та відносно осі

Вектор кількості руху матеріальної системи 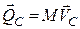визначає її поступальний рух. Обертальний рух матеріальної системи відносно центра 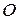визначається іншою векторною величиною – кінетичним моментом механічної системи або, так званим, головним моментом кількості руху механічної системи .

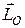Кінетичним моментом механічної системи або головним моментом кількості руху механічної системи відносно деякого центраназивається векторна величина, яка дорівнює геометричній сумі моментів кількостей рухів усіх точок системи відносно того самого центра:

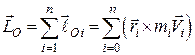. (27.1)

Кінетичним моментом механічної системи або головним моментом кількості руху механічної системи відносно деякої осі називається скалярна величина, яка дорівнює алгебраїчній сумі моментів кількостей рухів усіх точок механічної системи відносно тієї самої осі.

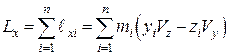. (27.2)

Залежність між кінетичним моментом механічної системи відносно центра 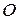і осі, наприклад, 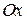, яка проходить через центр, має вигляд

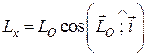. (27.3)

27.2. Кінетичний момент тіла, що обертається навколо нерухомої осі, відносно цієї осі

Запишемо моменти кількості руху кожної точки тіла, що обертається з кутовою швидкістю 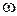відносно осі 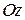(рис. 27.1).

.

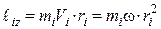
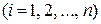Тоді кінетичний момент тіла, яке обертається навколо нерухомої осі, має такий вигляд:

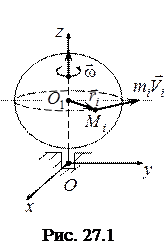
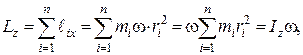
де

.

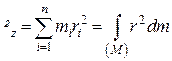Отже, кінетичний момент тіла, яке обертається навколо нерухомої осі, дорівнює добутку моменту інерції тіла відносно осі обертання і кутової швидкості його обертання.

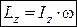. (27.4)

27.3. Теорема про зміну кінетичного моменту механічної системи.

Векторна похідна за часом від кінетичного моменту механічної системи відносно деякого центра дорівнює головному моменту зовнішніх сил, прикладених до точок механічної системи, відносно того самого центра.

Доведення: Розглянемо механічну систему, яка складається з 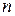матеріальних точок, на які діють зовнішні і внутрішні сили. Теорема про зміну моменту кількості руху для 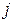-ої точки системи відносно деякого нерухомого центра 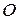має вигляд:

.

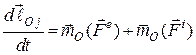
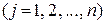Запишемо таких рівнянь стільки, скільки точок має дана система, підсумуємо їх:

.

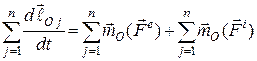Перетворимо ліву частину цього рівняння і, з урахуванням (27.1), отримуємо

.

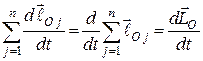Враховуючи, що 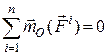остаточно маємо:

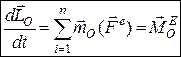. (27.5)

Рівняння (27.5) визначає теорему про зміну кінетичного моменту механічної системи відносно нерухомого центра.

Проектуючи обидві частини рівняння (27.5) на координатні осі, дістаємо:

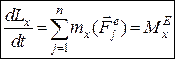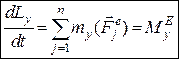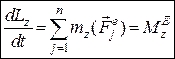; ; . (27.6)

Отже, перша похідна за часом від кінетичного моменту механічної системи відносно деякої осі дорівнює головному моменту зовнішніх сил, прикладених до точок механічної системи, відносно тієї самої осі.

Наслідки з теореми:

1. Внутрішні сили безпосередньо не впливають на зміну кінетичного моменту механічної системи. (Вони можуть здійснювати лише непрямий вплив через зовнішні сили).

2. Якщо головний момент всіх зовнішніх сил системи відносно деякого центра дорівнює нулю, то кінетичний момент механічної системи відносно того самого центра є векторною сталою величиною, тобто якщ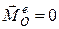о , то .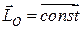

3. Якщо головний момент зовнішніх сил системи відносно будь-якої осі дорівнює нулю, то кінетичний момент механічної системи відносно тієї самої осі є сталою величиною, тобто якщ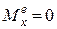о , то .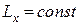

Другий та третій наслідки називаються відповідно законами збереження кінетичних моментів механічної системи відносно центра і осі.

При розв’язанні багатьох задач динаміки рух механічної системи відносно інерціальної системи відліку раціонально представляти як складний рух, що розкладається на переносний (поступальний) разом із центром мас і відносний (обертальний) рух навколо центра мас.

Зауваження: теорему про зміну кінетичного моменту механічної системи для відносного руху системи, записують вважаючи центр мас (т. С) нерухомим:

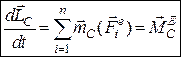. (27.7)

27.4. Збереження кінетичного моменту механічної системи

Розглянемо механічну систему, яка обертається навколо нерухомої осі. Якщо при цьому головний момент усіх зовнішніх сил відносно осі обертання дорівнює нулю, то кінетичний момент механічної системи відносно цієї осі є сталою величиною, тобто .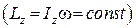

Якщо механічна система незмінна, то момент інерції її відносно осі обертання буде сталим і обертання системи відбувається зі сталою кутовою швидкістю.

Якщо механічна система змінна, тоді під дією внутрішніх або зовнішніх сил окремі її точки можуть наближатись чи віддалятись від осі обертання, що призведе до зменшення або збільшення моменту інерції І_z.

При цьому кінетичний момент системи відносно осі обертання і в цьому випадку повинен бути сталим. Тому зменшення момента інерції системи призведе відповідно до збільшення кутової швидкості і навпаки, тобто

,

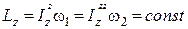звідки:

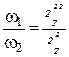. (27.8)

Умова (27.8) наочно демонструється на пристрої, що зветься платформою Жуковського. Цей пристрій являє собою круглу горизонтальну платформу, що обертається навколо центральної вертикальної осі з малим тертям.

Платформі з людиною, що знаходиться на ній, надають обертального руху. Оскільки на дану механічну систему діють тільки вертикальні сили (сили тертя досить малі), то їх моменти відносно осі обертання дорівнюють нулю. Дорівнюють нулю і моменти реакцій в’язей, оскільки вони перетинають вісь. Розводячи руками в боки, людина збільшує момент інерції механічної системи, що призводить до відповідного зменшення кутової швидкості платформи. Досить ефектно зміни кутової швидкості використовуються в балеті і фігурному катанні.

27.5. Приклад розв’язання задачі

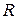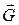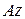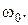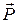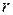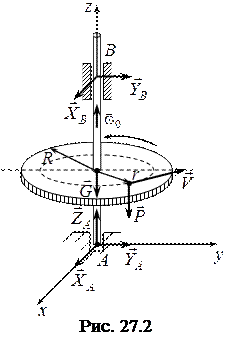
Кругла однорідна горизонтальна платформа радіуса і вагою обертається без тертя навколо вертикальної осі з кутовою швидкістю На платформі на відстані r від осі обертання стоїть людина вагою . Чому буде дорівнювати кутова швидкість платформи, якщо людина почне рухатись вздовж платформі за колом радіуса з відносною швидкістю 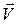в напрямку обертання платформи (рис. 27.2).

Розв’язання. На механічну систему, яка складається з платформи і людини, діють зовнішні сили: сили ваги платформи 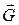і людини 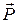, а також реакції в’язей в точках 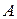і .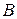

Головний момент зовнішніх сил відносно осі 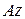дорівнює нулю, оскільки сили ваги паралельні цій осі, а реакції в’язей перетинають цю вісь. Отже, виконується закон збереження кінетичного моменту системи відносно осі :

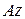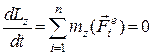
і тому

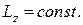
Кінетичний момент механічної системи відносно осі 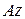у початковий момент часу коли людина відносно платформи не рухається, дорівнює:

,

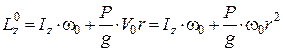де 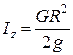– момент інерції платформи – круглого диска; 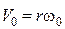– швидкість людини, яка нерухома по відношенню до платформи.

Кінетичний момент у випадку, коли людина рухається платформою з відносною швидкістю 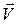, дорівнює:

.

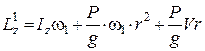Зважаючи на те, що виконується закон збереження кінетичного моменту системи відносно осі 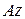, запишемо 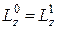, тоді:

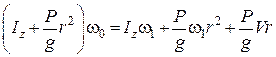
або

.

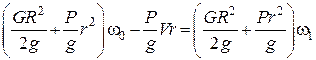Звідки

.

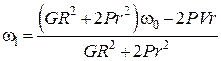РОБОТА СИЛИ ТА КІНЕТИЧНА ЕНЕРГІЯ МАТЕРІАЛЬНОЇ ТОЧКИ МАТЕРІАЛЬНОЇ СИСТЕМИ

Лекція 28

Робота сили ТА ЇЇ Потужність

28.1. Формули визначення роботи сили та її потужності потужності

У динаміці розглядається два випадки перетворення механічного руху.

У першому випадку механічний рух переноситься з однієї матеріальної системи на іншу у вигляді механічного руху.

У другому випадку механічний рух перетворюється в інші форми руху матерії (теплоту, електрику, потенціальну енергію і т.п.).

Кількісною міроюдії сили при перетворенні механічного руху в інші форми руху є робота сили А.

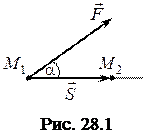Якщо сила стала за модулем і напрямом, а точка її прикладання переміщується прямолінійно (рис. 28.1), то робота сили дорівнює добутку модуля вектора сили на довжину вектора переміщення 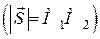і на косинус кута 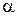між напрямом вектора сили і вектора переміщення:

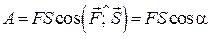. (28.1)

Якщ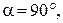о то 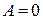; якщ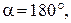о то .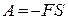

З векторної алгебри відомо, що скалярний добуток двох векторів дорівнює добутку модулів цих векторів на косинус кута між ними:

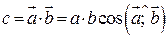. (28.2)

Тому, рівняння (28.1), враховуючи (28.2) набуває вигляду:

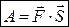, (28.3)

Отже, робота сили, яка стала за модулем і напрямом та точка прикладення якої рухається прямолінійно, дорівнює скалярному добутку вектора сили та вектора переміщення точки її прикладення.

Якщо сила змінна за модулем і напрямом, а точка її прикладання рухається за криволінійною траєкторією, то криволінійне переміщення точки прикладання сили розбивають на елементарні (нескінченно малі) ділянки 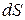. Далі обчислюють роботу сили на кожній елементарній ділянці, вважаючи силу сталою, а переміщення 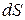– прямолінійним.

А потім визначають інтегральну суму елементарних робіт на даному переміщенні .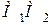

Елементарну роботу сили позначимо символом 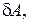а не 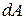, оскільки в загальному випадку вона не є диференціалом функції:

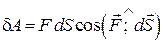. (28.4)

Використовуючи (28.3), рівняння (28.4) можна записати у вигляді:

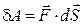. (28.5)

Оскільки вектор переміщення 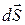дорівнює прирощенню 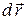радіуса – вектора точки прикладання сили 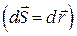(рис. 28.2), то рівняння (28.5) набуває вигляду:

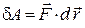. (28.6)

Аналітичний вираз для обчислення елементарної роботи отримаємо з рівняння (28.6), виразивши вектор сили і вектор переміщення 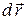через проекції на координатні осі:

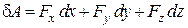. (28.7)

Повна робота сили на переміщенні 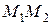визначається за формулами:

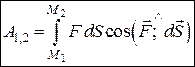; (28.8)

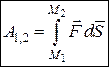; (28.9)

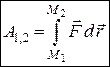; (28.10)

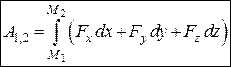. (28.11)

Поряд з поняттям роботи сили вводять також поняття її потужності.

Потужність сили дорівнює роботі, яка виконується за одиницю часу. Тому з урахуванням формул (28.5) або (28.8), маємо:

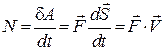
або

.

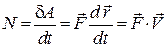Отже, потужність сили дорівнює скалярному добутку вектора сили та вектора швидкості руху точки її прикладання:

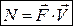. (28.12)

Таким чином, потужність N – це фізична величина, що характеризує швидкість виконання роботи силою, яка прикладена до матеріальної точки.

28.2. Теорема про роботу рівнодійної:

Робота рівнодійної на деякому переміщенні дорівнює алгебраїчній сумі робіт складових сил на тому самому переміщенні.

Нехай точка знаходиться під дією сил 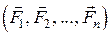. Оскільки ці сили утворюють збіжну систему сил, дію цих сил на дану точку можна замінити їх рівнодійною , яка дорівнює геометричній сумі заданих сил:

.

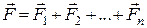Домножимо обидві частини цього рівняння скалярно на вектор 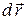елементарного переміщення точки :

.

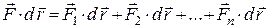Обчисливши інтегральні суми вздовж всього переміщення точки 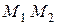, маємо:

,

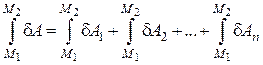остаточно:

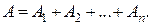
Теорему доведено.

28.3. Теорема про роботу внутрішніх сил незмінної системи

На будь-якому скінченому переміщенні сума робіт усіх внутрішніх сил абсолютно твердого тіла дорівнює нулю

Силу ваги 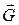матеріальної точки поблизу земної поверхні можна вважати сталою. Вона дорівнює добутку маси точки (тіла) на прискорення вільного падіння, тобто 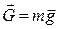і спрямована вертикально вниз.

Направимо вісь 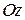вертикально вгору (рис. 28.3) та скористаємось аналітичним виразом елементарної роботи сили.

Проекції сили ваги 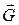на осі координат:

; ; .

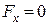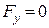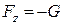Повна робота сили ваги на переміщенні :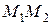

.

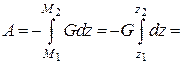
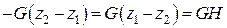Тут через 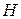позначена відстань вздовж вертикалі між горизонтальними площинами, проведеними через початкове і кінцеве положення точки .

Отже, робота сили ваги дорівнює взятому з відповідним знаком добутку сили ваги на вертикальне переміщення точки її прикладення:

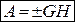. (28.13)

Робота сили ваги не залежить від довжини та форми траєкторії руху точки її прикладання, а залежить тільки від відстані між горизонтальними площинами, які проходять через початкове та кінцеве положення точки.

28.5. Робота сили пружності на скінченому прямолінійному переміщенні

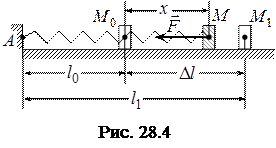Розглянемо матеріальну точку, яка прикріплена до вільного кінця горизонтальної пружини (рис. 28.4). За початок відліку системи 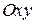візьмемо положення точки 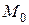, що відповідає недеформованій пружині, тобто коли точка 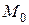знаходиться від точки 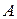на відстані 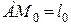. Якщо розтягувати пружину, то на точку діятиме змінна за модулем сила пружності пружини 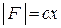, яка спрямована до точки .

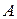Визначимо роботу, яку здійснює сила пружності на переміщенні :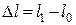

.

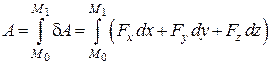Проекції сили пружності на координатні осі:

; ; .

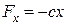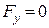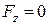Тоді

.

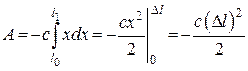При стисканні пружини знак роботи сили пружності буде додатним.

Отже, робота сили пружності дорівнює взятій з відповідним знаком половині добутку коефіцієнта пружності на квадрат деформації пружини.

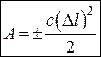. (28.14)

Аналогічно, легко довести, що робота сили пружності спіральної пружини при її кутовій деформації, дорівнює взятій з відповідним знаком половині добутку коефіцієнта пружності на квадрат деформації пружини.

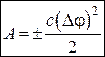. (28.15)

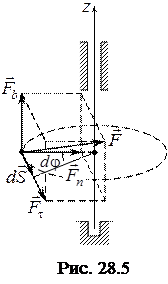28.6. Робота і потужність сили, прикладеної до твердого тіла, що обертається навколо нерухомої осі

Обчислимо елементарну роботу 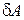сили , прикладеної до тіла, що обертається навколо нерухомої осі на переміщенні 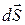, яке обумовлене поворотом тіла на елементарний кут .

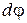Розкладемо силу на складові за натуральними осями (рис. 26.5):

.

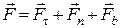На підставі теореми про роботу рівнодійної, робота сили буде дорівнювати сумі робіт її складових , , .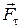

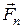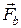Робота складових 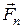і 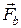, що перпендикулярні до переміщення 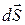, дорівнює нулю. Тому елементарна робота сили дорівнюватиме:

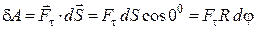. (28.16)

Визначимо момент сили відносно осі обертання, як суму моментів її складових. Оскільки складова 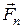паралельна осі, а складова 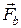перетинає цю вісь, тому вони момента відносно осі не утворюють.

Отже, маємо:

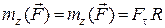. (28.17)

Враховуючи (26.17), рівняння (26.16) запишемо у вигляді

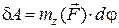. (28.18)

Отже, елементарна робота сили, прикладеної до твердого тіла, що обертається навколо нерухомої осі, дорівнює добутку моменту цієї сили відносно нерухомої осі обертання на елементарний приріст кута повороту тіла.

Повна робота сили на кінцевому переміщенні вздовж дуги кола дорівнює:

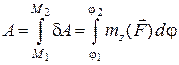. (28.19)

Якщо 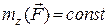, а 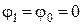, то маємо:

Дата добавления: 2014-12-25