
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Робота сили ваги 5 страница
|
|
|
|
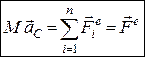 . (25.5)
. (25.5)
Рівняння (25.5) визначає доведену теорему про рух центра мас.
Проектуючи обидві частини (25.5) на координатні осі, дістаємо диференціальні рівняння руху координат центра мас:
 ;
; 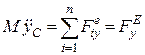 ;
;  . (25.6)
. (25.6)
З теореми випливають такі наслідки:
1. Внутрішні сили безпосередньо не впливають на рух центра мас механічної системи. (Вони можуть здійснювати лише непрямий вплив через зовнішні сили).
2 Якщо головний вектор всіх зовнішніх сил, які діють на точки механічної системи, весь час дорівнює нулю, то центр мас механічної системи перебуває в стані спокою або рухається рівномірно і прямолінійно.
Кінематичний стан центра мас при цьому залежить відпочаткової швидкості.
3. Якщо проекція головного вектора всіх зовнішніх сил на будь-яку вісь дорівнює нулю, то проекція центра мас механічної системи на цю вісь залишається нерухомою або рухається рівномірно і прямолінійно.
Другий та третій наслідки називаються законами збереження руху центра мас механічної системи.
25.2. Імпульс сили та його проекції на координатні осі
Спостереження вказують на те, що одна і та сама сила може різним тілам надати однакові кінематичні стани, але при цьому час дії сили на ці тіла повинен бути різним.
Дію сили на матеріальну точку за деякий проміжок часу можна визначити імпульсом сили.
Імпульс сили характеризує передачу матеріальній точці механічного руху за деякий проміжок часу з боку інших тіл, з якими взаємодіє дана матеріальна точка.
Якщо сила, що діє на матеріальну точку, є сталою за модулем і напрямом, то імпульс сили за проміжок часу 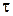 дорівнює добутку вектора сили на проміжок часу τ і має напрям цієї сили, тобто:
дорівнює добутку вектора сили на проміжок часу τ і має напрям цієї сили, тобто:
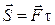 , (25.7)
, (25.7)
де
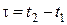 .
.
Якщо сила, що діє на точку, змінюється з плином часу за модулем чи напрямом, то проміжок часу 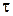 розбивають на елементарні проміжки часу, вважаючи при цьому силу сталою, а потім обчислюють інтегральну суму елементарних імпульсів
розбивають на елементарні проміжки часу, вважаючи при цьому силу сталою, а потім обчислюють інтегральну суму елементарних імпульсів
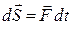 ; (25.8)
; (25.8)
 . (25.9)
. (25.9)
Проектуючи обидві частини (23.9) на координатні осі маємо:
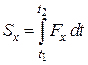 ;
; 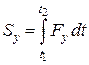 ;
; 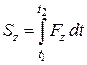 . (25.10)
. (25.10)
Отже, проекція імпульсу сили на вісь дорівнює імпульсу проекції сили на цю вісь.
Модуль і напрям імпульсу сили визначаєтьсязаформулами:
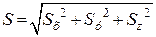 ;
;
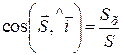 ;
;  ;
;  . (25.11)
. (25.11)
25.3. Теорема про зміну кількості руху матеріальної точки.
Кількістю руху або векторною мірою механічного руху матеріальної точки називається вектор 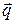 , який дорівнює добутку маси точки на вектор її швидкості і має напрям вектора швидкості
, який дорівнює добутку маси точки на вектор її швидкості і має напрям вектора швидкості
 . (25.12)
. (25.12)
 Запишемо основне рівняння руху матеріальної точки
Запишемо основне рівняння руху матеріальної точки 
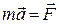 і перетворимо його ліву частину
і перетворимо його ліву частину
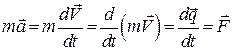 .
.
Отже,
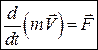 . (25.13)
. (25.13)
В правій частині цього рівняння силу  можна розглядати як окрему силу, або як рівнодійну кількох сил, що діють на матеріальну точку (рис. 23.2).
можна розглядати як окрему силу, або як рівнодійну кількох сил, що діють на матеріальну точку (рис. 23.2).
Рівняння (25.13) визначає теорему про зміну кількості руху матеріальної точки в диференціальній формі:
Векторна похідна за часом від кількості руху матеріальної точки дорінює вектору сили, яка діє на матеріальну точку.
Розділимо змінні в рівнянні (25.13) і зінтегруємо обидві його частини, після цього отримаємо:
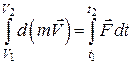
або
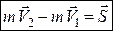 . (25.14)
. (25.14)
Рівняння (25.14) визначає теорему про зміну кількості руху матеріальної точки в інтегральній (скінченій) формі:
Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнює імпульсу сили, що діє на точку, за той самий проміжок часу.
Проектуємо обидві частини рівняння (23.14) на координатні осі:
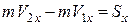 ;
; 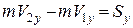 ;
;  . (25.15)
. (25.15)
Отже, зміна проекції кількості руху матеріальної точки за деякий проміжок часу дорівнює проекції імпульсу сили, що діє на точку, за той самий проміжок часу і на ту саму вісь.
25.4 Теорема про зміну головного вектора кількості руху механічної системи
Головним вектором кількості руху механічної системи називається векторна величина, що дорівнює геометричній сумі кількості рухів матеріальних точок, які складають механічну систему:
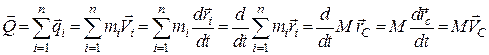 .
.
Отже, головний вектор  кількості руху механічної системи дорівнює добутку маси системи на вектор швидкості її центра мас і має напрям цього вектора:
кількості руху механічної системи дорівнює добутку маси системи на вектор швидкості її центра мас і має напрям цього вектора:
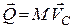 . (25.16)
. (25.16)
Розглянемо механічну систему, яка складається з n матеріальних точок. Нехай на точки цїєї системи діють зовнішні (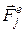 ) та внутрішні (
) та внутрішні ( ) сили.
) сили.
Тоді теорема про зміну кількості руху для j- ої точки цієї системи в диференціальній формі матиме вигляд:
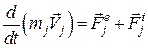 . (25.17)
. (25.17)
Запишемо таких рівнянь стільки, скільки точок має дана система 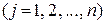 та підсумуємо їх:
та підсумуємо їх:
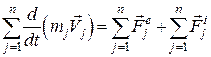 . (25.18)
. (25.18)
Перетворимо ліву частину рівняння (23.18):
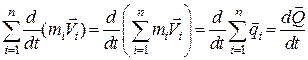 . (25.19)
. (25.19)
Підставивши отримане значення (23.18) в (23.19) та враховуючи, що 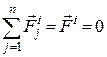 , остаточно маємо:
, остаточно маємо:
 . (25.20)
. (25.20)
Рівняння (25.20) визначає теорему про зміну головного вектора кількості руху механічноїсистеми в диференціальній формі.
Векторна похідна за часом від головного вектора кількості руху механічної системи дорівнює геометричній сумі всіх зовнішніх сил, прикладених до точок системи, або головному вектору всіх зовнішніх сил, які діють на точки механічної системи.
Проектуємо обидві частини рівняння (23.20) на осі декартової системи координат:
 ;
; 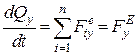 ;
; 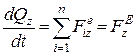 . (25.21)
. (25.21)
Отже, перша похідна за часом від проекції головного вектора кількості руху механічноїсистеми на будь-яку вісь дорівнює алгебраїчній сумі проекцій зовнішніх сил, які діють на точки механічної системи, або проекції головного вектора зовнішніх сил на ту саму вісь.
Для отримання теореми про зміну кількості руху механічної системи в інтегральній (скінченій) формі використаємо рівняння (25.21).
Домножимо обидві його частини на 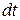 і зінтегруємо в межах від
і зінтегруємо в межах від 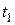 до
до 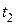 :
:
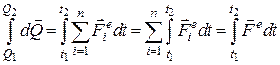 .
.
Після інтегрування остаточно дістанемо:
 . (25.22)
. (25.22)
Рівняння (25.22) визначає теорему про зміну головного вектора кількості руху механічної системи:
Зміна головного вектора кількості руху механічної системи за деякий проміжок часу дорівнює геометричній сумі імпульсів зовнішніх сил, які діють на точки механічної системи за той самий проміжок часу, або повному імпульсу головного вектора зовнішніх сил.
Спроектувавши обидві частини рівняння (25.22) на координатні осі дістанемо:
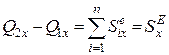 ;
; 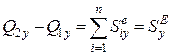 ;
; 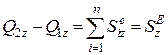 . (25.23)
. (25.23)
Отже, зміна проекції головного вектора кількості руху механічної системи на будь яку вісь за деякий проміжок часу дорівнює алгебраїчній сумі проекцій імпульсів зовнішніх сил, що діють на точки механічної системи за той самий проміжок часу і на ту саму вісь, або проекції повного імпульсу головного вектора зовнішніх сил на цю вісь.
Наслідки з теореми:
1. Внутрішні сили безпосередньо не впливають на зміну головного вектора кількості руху механічної системи.
2. Якщо головний вектор усіх зовнішніх сил, які діють на точки механічної системи, дорівнює нулю, то головний вектор кількості руху цієї системи є векторною сталою величиною 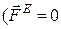 ;
; 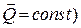 .
.
3. Якщо проекція головного вектора зовнішніх сил, що діють на точки механічної системи, на будь-яку вісь дорівнює нулю, то проекція головного вектора кількості руху механічної системи на ту саму вісь є сталою величиною(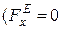 ;
;  .
.
Другий і третій наслідки називаються законами збереження кількості руху механічної системи.
25.5. Приклади розв’язання задач
Приклад 1. Людина вагою  стоїть на кормі човна вагою
стоїть на кормі човна вагою 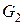 і довжиною
і довжиною 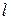 , що перебуває в стані спокою (рис. 23.3). Визначити відстань
, що перебуває в стані спокою (рис. 23.3). Визначити відстань 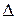 , на яку переміститься човен, якщо людина перейде на ніс човна. Опором води знехтувати.
, на яку переміститься човен, якщо людина перейде на ніс човна. Опором води знехтувати.
 Розв’язання. На човен діють зовнішні сили, до яких належать сили ваги човна
Розв’язання. На човен діють зовнішні сили, до яких належать сили ваги човна 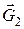 і людини
і людини 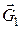 , а також архімедова сила
, а також архімедова сила 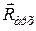 , лінія дії якої проходить через центр мас механічної системи, що складається з човна та людини.
, лінія дії якої проходить через центр мас механічної системи, що складається з човна та людини.
Оскільки зовнішні сили вертикальні, то проекція головного вектора зовнішніх сил на вісь 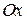 дорівнює нулю. Отже, виконується закон збереження кількості руху центра мас, тобто швидкість руху центра мас є стала величина
дорівнює нулю. Отже, виконується закон збереження кількості руху центра мас, тобто швидкість руху центра мас є стала величина 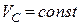 .
.
Оскільки система на початку руху перебувала в стані спокою 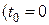 ,
,  ), то координата
), то координата 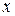 центра мас протягом руху залишається незмінною
центра мас протягом руху залишається незмінною 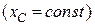 , тобто
, тобто
виконується умова 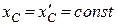 .
.
Це можливо лише в тому випадку, якщо при русі людини праворуч, човен переміщується ліворуч.
Визначимо координату  і
і 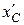 центра мас системи в початковий і кінцевий моменти часу:
центра мас системи в початковий і кінцевий моменти часу:
 ;
; 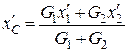 .
.
Виразимо координати 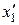 і
і 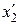 через
через 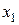 і
і  :
:
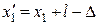 ;
; 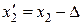 .
.
Тоді отримаємо:
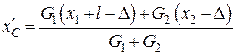 .
.
Оскільки 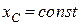 , то
, то  і тому:
і тому:
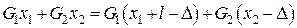 .
.
Звідки, після нескладних перетворень дістанемо:
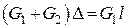 .
.
Остаточно
 .
.
Приклад 2. Швидкість корабля тоннажністю 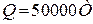 за час
за час  після зупинення роботи турбіни зменшилась на 3,6 км/год, тобто на 1м/с (рис. 25.4). Визначити середню силу опору води, вважаючи рух корабля прямолінійним.
після зупинення роботи турбіни зменшилась на 3,6 км/год, тобто на 1м/с (рис. 25.4). Визначити середню силу опору води, вважаючи рух корабля прямолінійним.
 |
Розв’язання: Враховуючи, що корабель здійснює поступальний рух, приймемо його за матеріальну точку. Вага корабля
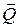 врівноважується силою Архімеда
врівноважується силою Архімеда 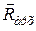 . Сполучимо вісь
. Сполучимо вісь 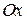 з прямолінійною траєкторією руху корабля.
з прямолінійною траєкторією руху корабля.
Скористаємось теоремою про зміну кількості руху матеріальної точки в проекції на вісь 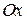 :
:
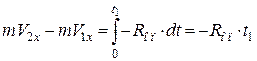 ,
,
звідки
 ,
, 
де 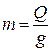 ; тоді
; тоді
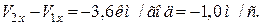
Приклад 3. На нерухомій горизонтальній платформі вагою 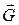 знаходиться людина вагою
знаходиться людина вагою 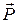 (рис. 25.5). В деякий момент часу людина почала рухатись вздовж платформи з відносною швидкістю
(рис. 25.5). В деякий момент часу людина почала рухатись вздовж платформи з відносною швидкістю 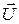 . Нехтуючи тертям між рейками і колесами, а також опором повітря, визначити закон зміни швидкості руху платформи.
. Нехтуючи тертям між рейками і колесами, а також опором повітря, визначити закон зміни швидкості руху платформи.
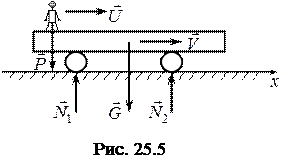 Розв’язання. Механічна система складається з платформи та людини. На систему діють активні зовнішні сили – сили ваги платформи
Розв’язання. Механічна система складається з платформи та людини. На систему діють активні зовнішні сили – сили ваги платформи 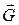 та людини
та людини 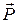 , а також реакції рейок
, а також реакції рейок 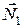 і
і 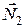 .
.
Сумістимо вісь з горизонтальною рейкою та застосуємо до розв’язування задачі теорему про зміну кількості руху механічної системи в проекції на цю вісь (в диференціальній формі).
 , тоді
, тоді  .
.
Отже, виконується закон збереження проекції кількості руху механічної системи. В початковий момент часу швидкість руху платформи.  і швидкість руху людини по платформі
і швидкість руху людини по платформі 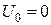 , тоді
, тоді 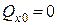 .
.
В момент 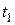 , коли людина почала рухатись вздовж платформи з відносною швидкістю
, коли людина почала рухатись вздовж платформи з відносною швидкістю 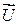 , абсолютна швидкість платформи дорівнює
, абсолютна швидкість платформи дорівнює 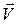 , а абсолютна швидкість людини
, а абсолютна швидкість людини 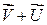 , тоді проекція на вісь
, тоді проекція на вісь 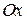 кількості руху механічної системи платформа – людина буде дорівнювати
кількості руху механічної системи платформа – людина буде дорівнювати
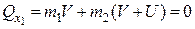 ,
,
оскільки 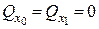 .
.
Звідси
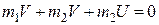 ;
;
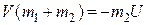 або
або 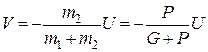 .
.
Знак «мінус» показує на те, що платформа рухається в бік протилежний руху людини.
Лекція 26
МОМЕНТ КІЛЬКОСТІ РУХУ МАТЕРІАЛЬНОЇ ТОЧКИ
26.1. Момент кількості руху матеріальної точки відносно центра і осі
Момент кількості руху матеріальної точкивідносно центравизначається так само, як і момент сили 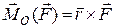 .
.
Момент кількості руху матеріальної точки відносно нерухомого центра 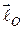 дорівнює векторному добутку радіуса-вектора точки
дорівнює векторному добутку радіуса-вектора точки 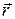 і вектора кількості руху точки
і вектора кількості руху точки  (рис. 26.1):
(рис. 26.1):
 . (26.1)
. (26.1)
За модулем:  .
.
Отже, моментом кількості руху матеріальної точки відносно деякого центра називається вектор 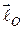 який дорівнює за модулем добутку модуля кількості руху точки
який дорівнює за модулем добутку модуля кількості руху точки 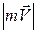 на плече d і має напрям перпендикулярний до площини, яка проходить через вектор
на плече d і має напрям перпендикулярний до площини, яка проходить через вектор  і центр О в той бік, звідки вектор
і центр О в той бік, звідки вектор  відносно центра О видно спрямованим проти руху годинникової стрілки (рис. 26.1).
відносно центра О видно спрямованим проти руху годинникової стрілки (рис. 26.1).
Величина момента кількості руху матеріальної точки відносно деякої осі, наприклад 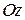 , записуються аналогічно відповідному виразу для момента сили (рис. 26.2):
, записуються аналогічно відповідному виразу для момента сили (рис. 26.2):
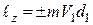 ; (26.2)
; (26.2)
Аналогічно запишемо таку залежність:
 |
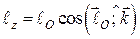 . (26.3)
. (26.3)
Отже, проекція вектор-моменту кількості руху матеріальної точки відносно деякого центра на вісь, яка проходить через цей центр, дорівнює моменту кількості руху точки відносно цієї осі.
Проектуючи вектор момент кількості руху 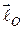 точки
точки  відносно центра
відносно центра 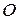 (26.1) на осі прямокутної декартової системи координат, отримаємо вирази для обчислення моментів кількості руху матеріальної точки відносно координатних осей:
(26.1) на осі прямокутної декартової системи координат, отримаємо вирази для обчислення моментів кількості руху матеріальної точки відносно координатних осей:
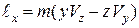 ;
; 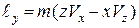 ;
; 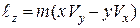 . (26.4)
. (26.4)
26.2. Теорема про зміну моменту кількості руху матеріальної точки:
Векторна похідна за часом від моменту кількості руху матеріальної точки відносно деякого центра дорівнює вектору-моменту сили, прикладеної до цієї точки, відносно того самого центра.
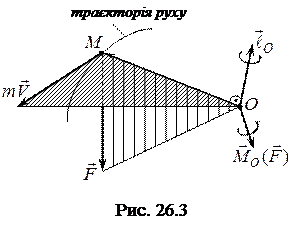 Доведення. Нехай матеріальна точка
Доведення. Нехай матеріальна точка  масою
масою  рухаєтьс я зішвидкістю
рухаєтьс я зішвидкістю  під дією сили
під дією сили  (рис. 26.3).
(рис. 26.3).
Момент кількості руху даної матеріальної точки  відносно нерухомого центра
відносно нерухомого центра  визначається за формулою (26.1):
визначається за формулою (26.1):
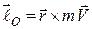 .
.
Знайдемо першу похідну за часом від останнього виразу
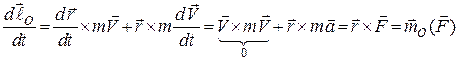 . (26.5)
. (26.5)
Тут  , як векторний добуток двох колінеарних векторів.
, як векторний добуток двох колінеарних векторів.
Остаточно маємо:
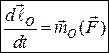 . (26.6)
. (26.6)
Рівність (26.6) визначає доведену теорему про зміну моменту кількості руху матеріальної точки відносно нерухомого центра.
Проектуючи обидві частини рівняння (26.6) на координатні осі, дістаємо:
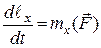 ,
, 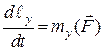 ,
, 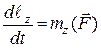 . (26.7)
. (26.7)

Отже, перша похідна за часом від моменту кількості руху матеріальної точки відносно деякої осі дорівнює моменту сили, прикладеної до точки, відносно тієї самої осі.
Наслідки з теореми:
1. Якщо момент сили, прикладеної до точки, відносно деякого центра за весь час руху дорівнює нулю, то вектор-момент кількості руху матеріальної точки відносно того самого центра є векторною сталою величиною:
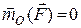 ;
; 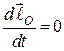 ;
; 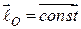 . (26.8)
. (26.8)
2. Якщо момент сили, прикладеної до точки, відносно деякої осі, наприклад 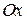 за весь час руху дорівнює нулю, то момент кількості руху матеріальної точки відносно тієї самої осі є сталою величиною:
за весь час руху дорівнює нулю, то момент кількості руху матеріальної точки відносно тієї самої осі є сталою величиною:
 ;
;  ;
; 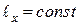 . (26.9)
. (26.9)
26.3. Рух матеріальної точки під дією центральної сили. Закон площин
 Сила, лінія дії якої весь час проходить через деякий нерухомий центр, називається центральною силою. Прикладом такої сили є сила притягання планет Сонячної системи до Сонця.
Сила, лінія дії якої весь час проходить через деякий нерухомий центр, називається центральною силою. Прикладом такої сили є сила притягання планет Сонячної системи до Сонця.
Розглянемо рух матеріальної точки  під дією сили
під дією сили  , лінія дії якої під час руху проходить через точку
, лінія дії якої під час руху проходить через точку 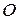 (рис. 26.4.).
(рис. 26.4.).
Вектор момент сили  відносно точки
відносно точки 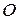 весь час дорівнює нулю і рівняння (26.6) матиме вигляд:
весь час дорівнює нулю і рівняння (26.6) матиме вигляд:
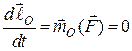 ,
,
звідки
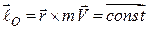 .
.
Оскільки маса точки розглядається як стала величина, то вектор-момент вектора швидкості 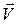 відносно центра
відносно центра 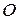 залишається незмінним, тобто
залишається незмінним, тобто
 . (26.10)
. (26.10)
Цей вектор весь час спрямований перпендикулярно до площини, яка утворюється за допомогою векторів 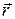 і
і 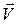 .
.
Оскільки вектор  зберігає незмінним не тільки модуль, а і напрям, то радіус-вектор
зберігає незмінним не тільки модуль, а і напрям, то радіус-вектор 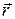 точки
точки  і вектор її швидкості
і вектор її швидкості 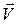 повинні весь час знаходитись в одній площині. З цього випливає, що траєкторією руху точки
повинні весь час знаходитись в одній площині. З цього випливає, що траєкторією руху точки  є плоска крива, а радіус вектор і швидкість точки
є плоска крива, а радіус вектор і швидкість точки  змінюються відповідно таким чином, що момент швидкості відносно центра
змінюються відповідно таким чином, що момент швидкості відносно центра 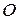 залишається під час руху незмінним.
залишається під час руху незмінним.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 444; Нарушение авторских прав?; Мы поможем в написании вашей работы!