Приклади розв’язання задач. Приклад 1. Рух точки задано рівняннями:

Приклад 1. Рух точки задано рівняннями:

; .

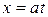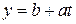Визначити рівняння траєкторії точки.

Розв’язання. 3 першого рівняння знайдемо час t і, підставляючи його значення у друге, одержимо рівняння траєкторії точки в координатній формі:

.

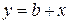Це рівняння прямої, але траєкторією буде не вся пряма, а тільки та її частина, по якій рухається точка. З рівнянь руху витікає, що на початку руху () точка 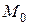мала координати 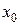=0, = b. Із збільшенням часу координати точки збільшуються.

Отже, траєкторією точки буде та частина прямої, яка на рис. 11.4 показана суцільною лінією.

Приклад 2. Рух точки задано у декартових координатах рівняннями:

; ,

де 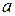, 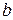і 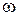– сталі. Перейти до натурального способу задання руху точки.

Розв’язання. Із заданих рівнянь вилучимо час 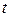. Для цього у першому рівнянні величину 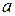переносимо в ліву частину. Далі, підносимо обидва рівняння у другий ступінь і додавши їх, отримаємо рівняння траєкторії точки у координатній формі: .

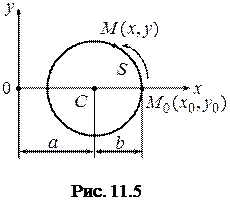Траєкторія точки – коло радіуса 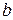, центр якого має координати (рис. 11.5).

При координати точки , , 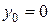тобто точка знаходилась в положенні 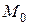. З рівнянь руху виходить, що за зростанням 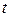координата 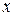зменшується, а координата 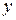збільшується. Отже, точка з початкового положення 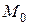рухається у напрямку, що показано стрілкою на рис. 11.5.

Обчислюємо похідні від заданих рівнянь:

; .

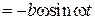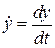
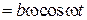За формулою (11.6) одержимо рівняння руху точки за траєкторією:

= .

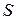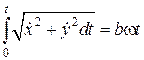Отже, точка описує коло радіуса b з центром С так, що її дугова координата 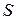збільшується пропорційно часу за лінійним законом.

Приклад 3. За заданими рівняннями руху точки

;

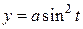
знайти рівняння її траєкторії, визначити цю траєкторію, а також знайти закон руху точки за траєкторією, відраховуючи відстань від початкового положення точки.

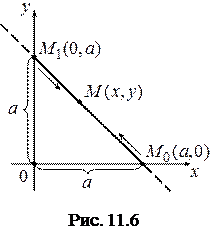Розв’язання. Рівняння траєкторії точки у координатній формі – рівняння прямої

.

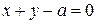Траєкторія точки – це відрізок прямої, позначений на рис. 11.6 суцільною лінією. Рух точки починається з положення 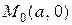. Через час 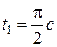точка займе положення 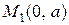, а через 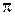повернеться у точку .

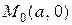Враховуючи формулу (11.6) знаходимо рівняння руху за траєкторією:

, ;

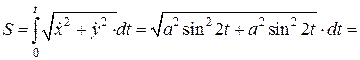
Отже, точка рухається вздовж відрізка в його межах за гармонійним законом, тобто відстань М відповідно збільшується або зменшується.

Приклад 4. Рух точки, що описує фігуру Ліссажу, задається рівняннями:

; .

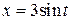Знайти рівняння траєкторії точки, побудувати цю траєкторію та визначити напрям руху точки у різні моменти часу. Знайти також найближчий після початку руху момент часу 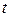, коли траєкторія перетинає вісь Ох.

Розв’язання. Враховуючи обмеження з рівнянь руху точки 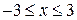; 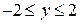, встановлюємо область розташування траєкторії точки (рис. 11.7).

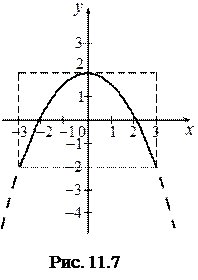Знайдемо рівняння траєкторії у координатній формі, вилучивши з рівнянь руху параметр 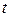. Для цього з першого рівняння виділимо:

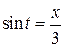
і піднесемо до квадрату:

.

Використовуючи формулу з тригонометрії

,

запишемо:

.

Звідки отримуємо:

.

Це рівняння квадратної параболи з вертикальною віссю симетрії .Траєкторієюточки є верхівка цієї параболи, що знаходиться у середині визначеної областіі показана на рис. 11.7 суцільною лінією.

Момент часу 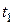– момент перетину точкою 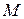осі після початку руху відповідає координаті

.

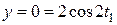Враховуючи, що 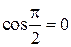, маємо:

; ,

тобто

.

Дата добавления: 2014-12-25