Визначення швидкостей точок плоскої фігури за допомогою МЦШ

Лекція 17

Проекції швидкостей двох точок плоскої фігури на пряму, що проходить через ці точки, рівні між собою.

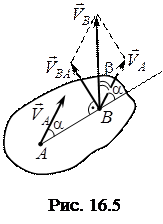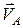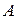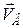Розглянемо рух плоскої фігури у її площині (рис. 16.5). Нехай – швидкість точки , а – швидкість точки 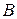. Приймаючи точку 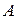за полюс і використовуючи теорему про швидкості точок плоскої фігури (16.4), отримаємо:

,

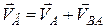де .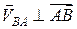

Проектуючи обидві частини цієї рівності на пряму АВ, одержимо

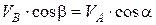, (16.7)

що і виражає сформульовану вище теорему.

Ця теорема дозволяє знайти швидкість точки плоскої фігури, якщо відомий напрям її швидкості, а також відома швидкість іншої точки цієї плоскої фігури за величиною і напрямом.

17.1. Теорема про миттєвий центр швидкостей (МЦШ):

При непоступальному русі плоскої фігури у своїй площині в кожний момент часу існує точка, швидкість якої по відношенню до плоскої фігури в цей момент часу дорівнює нулю.

Ця точка позначається літерою 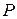і називається миттєвим центром швидкостей (МЦШ). Під час руху плоскої фігури точка безперервно змінює своє положення.

Отже, миттєвий центр швидкостей є точкою перетину миттєвої осі обертання з площиною руху.

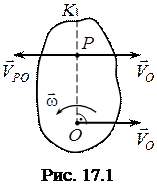
Уявімо собі плоску фігуру, яка рухається в своїй площині (рис. 17.1).

Припустимо, що в даний момент часу відома швидкість 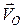точки 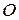і кутова швидкість обертання плоскої фігури навколо точки .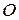

Візьмемо точку 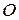за полюс і знайдемо ту точку 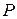плоскої фігури, швидкість якої у даний момент часу дорівнює нулеві.

Для цього повернемо пряму, по якій направлений вектор 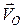, на прямий кут у бік обертання плоскої фігури. На цій прямій 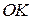на відстані 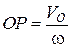від полюса визначимо точку 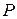. Використовуючи ,

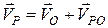знайдемо швидкість точки 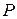. Причому швидкість 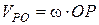і спрямована перпендикулярно 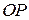у бік обертання. Отже, швидкість 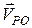в обертальному русі точки 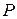навколо полюса 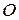спрямована в протилежний бік швидкості 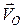полюса 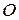, перенесеної в точку .

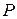Тоді ці вектори, що діють по одній прямій, додаються алгебраїчно:

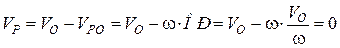, тобто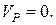

Отже, доведено, що миттєвий центр швидкості плоскої фігури лежить на перпендикулярі до швидкості 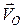, на відстані 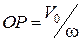від полюса .

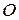Миттєвий центр швидкості є єдиною точкою плоскої фігури для даного моменту часу. В інший момент часу миттєвим центром швидкості для неї буде вже інша точка.

Наслідок І. Якщо прийняти миттєвий центр швидкостей за полюс, то рух плоскої фігури в даний момент часу можна розглядати як обертальний навколо миттєвої осі, яка перпендикулярна до плоскої фігури і проходить через миттєвий центр швидкості (МЦШ).

Припустимо, що миттєвий центр швидкостей 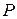відомий. Тоді, прийнявши точку 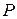за полюс і враховуючи, що в цьому випадку швидкість його 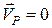, знайдемо швидкість довільної точки :

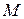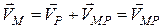, (17.1)

Тут 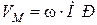і спрямований вектор 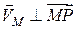у бік обертання.

Для будь-якої іншої точки 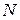можна записати аналогічно:

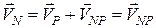, (17.2)

Тут 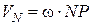і спрямований вектор 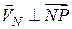у бік обертання.

Наслідок ІІ. Швидкості точок плоскої фігури пропорційні відстаням до миттєвого центру швидкостей і направлені перпендикулярно до відрізків, які з'єднують ці точки з миттєвим центром швидкостей, у бік обертання плоскої фігури

З формул (17.1) і (17.2), які визначають абсолютне значення швидкостей точок плоскої фігури, виходить що:

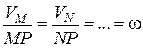. (17.3)

Отже, швидкості точок плоскої фігури розподіляються пропорційно відстаням цих точок до миттєвого центра швидкостей.

Дата добавления: 2014-12-25