Термодинамічний процес (незамкнутий цикл)

· Розглянемо оборотній цикл 1a2b1, в якому 1a2 – оборотній процес і 2b1 – теж оборотній процес (рис. 6.8). Для оборотнього циклу запишемо інтеґрал Клаузіуса:

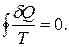(6.75)

Рис. 6.8. Схема циклу для означення термодинамічних процесів

Розіб’ємо цей інтеґрал на частини:

(6.76)

і представимо вираз (6.76) у вигляді:

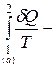
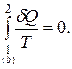(6.77)

Тоді

. (6.78)

За означенням інтеґрал (6.78) є зміна ентропії в кінцевому процесі 1→2:

(S₂ – S₁). (6.79)

· Висліди з (6.79):

1) зведене тепло 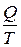для оборотнього процесу є параметром термодинамічного стану;

2) при адіабатному процесі (δQ=0)

(S₂ – S₁)= ΔS= 0 (6.80)

тобто для ізольованої системи зміна ентропії в оборотньому процесі дорівнює нулю;

3) при ізотермному процесі (Т=const)

(6.81)

· Нехай цикл 1a2b1 необоротній (рис. 6.8), при цьому процес 1a2 – необоротній, а 2b1 – оборотній.

Запишемо другий інтеґрал Клаузіуса для необоротнього циклу:

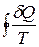<0. (6.82)

Розіб’ємо (6.82) на два інтеґрали:

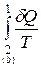<0 (6.83)

і представимо вираз (6.83) у вигляді:

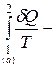
<0. (6.84)

Звідки

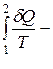(S₂ – S₁) <0, (6.85)

<(S₂ – S₁). (6.86)

· Висліди з (6.86):

1) зведене тепло 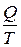для необоротнього процесу не є параметром термодинамічного стану;

2) при адіабатному процесі (δQ=0)

(S₂ – S₁)>0 – принцип зростання ентропії в ізольованій системі;

3) таким чином, для ізольованої системи зростання ентропії визначає напрямок самочинного процесу і досягнення рівноваги при

(S₂ – S₁)≥0; (6.87)

і у цьому полягає фізичний смисл ентропії;

4) при ізотермному процесі (Т=const)

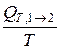< (S₂ – S₁); (6.88)

5) різниця

Δ=(S₂ – S₁) – 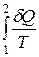(6.89)

визначає ступінь відхилення необоротнього процесу від оборотнього і в цьому полягає термодинамічний смисл ентропії.

Дата добавления: 2014-12-25