Ентропія, внутрішня енергія і ентальпія як характеристичні функції

ОЗНАЧЕННЯ ХАРАКТЕРИСТИЧНИХ ФУНКЦІЙ І ТЕРМОДИНАМІЧНИХ ПОТЕНЦІАЛІВ

Лекція 7

ХАРАКТЕРИСТИЧНІ ФУНКЦІЇ. ТЕРМОДИНАМІЧНІ ПОТЕНЦІАЛИ. ТЕРМОДИНАМІЧНА РІВНОВАГА

Характеристичні функції. Термодинамічні потенціали. Ізохорно-ізотермний потенціал Гельмгольца. Ізобарно-ізотермний потенціал Ґіббса. Утворення термодинамічних потенціалів Гельмгольца і Ґіббса за допомогою термодинамічних функцій. Співвідношення між термодинамічними параметрами і характеристичними функціями.

Умови термодинамічної рівноваги. Критерії рівноваги і оборотности. Рівняння Гельмгольца. Рівняння Ґіббса. Рівняння Ґіббса-Гельмгольца.

1. У хемічній термодинаміці для визначення характеристик процесів застосовують різні термодинамічні функції, які отримали назву характеристичних функцій.

Термодинамічними характеристичними функціями називають функції термодинамічного стану, за величинами яких або їх похідних можна визначити термодинамічний стан у явній формі і розрахувати будь-які термодинамічні величини. До таких функцій відносять: ентропію S, внутрішню енергію U, ентальпію H, «енергію» Гельмгольца F, «енергію» Ґіббса G тощо.

Ці функції набувають ознак характеристичних, якщо:

S=S (U, V) (7.1)

U=U (V,S) (7.2)

H=H (p, S) (7.3)

F=F (V, T) (7.4)

G=G (p, T) (7.5)

2. Поруч з ентропією S, зміною якої DS найбільше зручно характеризувати процеси в ізольованій системі, внутрішньою енергією та ентальпією, використовують термодинамічні потенціали, які дозволяють отримувати характеристики процесів при різних умовах їх проведення. U, H, F, G називають термодинамічними потенціалами.

1. Ентропія. Для ізольованої системи і протікання оборотніх (знак рівности) або необоротніх (знак нерівности) згідно другого начала термодинаміки:

, (7.6)

звідки TdS≥δQ. (7.7)

Для (7.6) із врахуванням першої форми запису першого начала термодинаміки для оборотніх процесів отримаємо диференціальне визначення ентропії S=S (U, V):

(7.8)

де pdV=δL – термодинамічна робота.

З (7.8) витікає:

· при U=const ; (7.9)

· при V=const 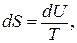; (7.10)

· при U, V=const 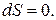(7.11)

Для нерівновагових процесів в ізольованих системах:

(7.12)

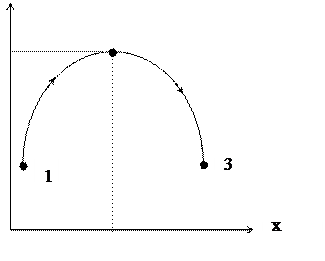
При умовах протікання процесів U, V=const dS≥0, при цьому граничний стан (рівновага при х₀) досягається при dS=0, d²S<0 (максимум S_max). Тобто в ізольованих системах при U, V=const самочинно відбуваються процеси, які супроводжуються зростанням ентропії (рис.7.1).

У таких системах при умовах U, V=const можливі процеси при dS<0, але вони протікають несамочинно і вимагають витрат енергії.

S

S_max

x₀

Рис.7.1. Самочинні (1→2) і несамочинні (2→3) процеси в ізольованих системах при U, V=const (тут х – хід процесу)

До числа термодинамічних потенціалів, що характеризують стан термодинамічної системи, відносять зокрема такі характеристичні фугкції:

2. Внутрішню енергію при виборі в якості основних незалежних змінних S і V:

U= U (S, V). (7.13)

Повний диференціал при цьому для U:

dU=TdS – pdV, (7.14)

· при S=const dU= – pdV, звідки , (7.15)

· при V=const dU= TdS, звідки . (7.16)

Для необоротного процесу:

dU≤TdS – pdV. (7.17)

3. Ентальпію при виборі в якості незалежних змінних S і р:

Н=Н (S, р).

Повний диференціал при цьому для Н:

dH=TdS+Vdp, (7.18)

· при S=const dH=Vdp, звідки , (7.19)

· при p=const dH= TdS, звідки (7.20)

Для необоротного процесу:

dH≤TdS+Vdp. (7.21)

Дата добавления: 2014-12-25