Ізохорно-ізотермний потенціал Гельмгольца

Із врахуванням другого начала термодинаміки, першої форми запису першого начала термодинаміки та лише термодинамічної роботи рівняння для нерівновагових процесів запишемо так:

TdS ³ dU + pdV. (7.22)

Враховуючи, що TdS = d(TS) – SdT,

рівняння (7.22) запишемо так:

d(TS) – SdT ³ dU+ pdV, (7.23)

звідки – SdT – pdV ≥ dU – d(TS). (7.24)

Зрозуміло, що

dU – d(TS) = d (U – TS). (7.25)

Тоді вираз (7.24) набуде вигляду:

– SdT – pdV ≥ d (U – TS).

Термодинамічну функцію F=(U – TS) називають ізохорно-ізотермним потенціалом (ізохорним потенціалом, потенціалом Гельмгольца, гельмгольцівським потенціалом, «вільною енергією»*, «енергією Гельмгольца»*, гельмгольцівською «енергією»*, «вільною енергією» при сталому об’ємі* тощо):

F = U – TS, (7.26)

* Терміни «вільна енергія», «енергія Гельмгольца», «гельмгольцівська енергія», «вільна енергія при сталому об’ємі» є некоректними і можуть викликати помилкове уявлення про існування особливої форми енергії. В дійсности це данина історії науки і ніякої особливої форми енергії, що відповідає термодинамічному ізохорно-ізотермному потенціалу F, в тілі не існує.

де (TS) – зв’язана частина внутрішньої енергії, яка в ізохорно-ізотермній системі при ізохорно-ізотермних процесах не може бути перетворена в роботу.

Повним диференціалом функції F є

dF = dU – TdS – SdT. (7.27)

Записавши (7.26) так

U = F + (TS), (7.28)

враховуючи, що в ізохорно-ізотермній системі робота може бути звершена тільки за рахунок зменшення F, можна стверджувати, що в такій системі в роботу може бути перетворена не вся внутрішня енергія, а тільки її «вільна» частина F.

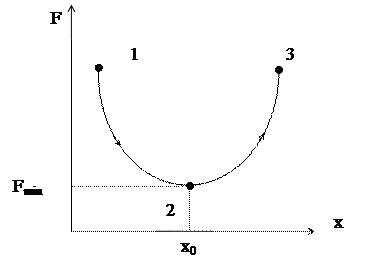Рис. 7.2. Самочинні (1→2) і несамочинні (2→3) процеси в системах при V,Т=const (тут х – хід процесу)

Таким чином, рівняння (7.24) для нерівновагових процесів запишемо так:

– SdT – pdV ≥ dF. (7.29)

Звідки витікає, що критерієм рівноваги системи, для якої V, T = const (ізохорно-ізотермна система), є умови:

dF £ 0, (7.30)

тобто, з наближенням до стану рівноваги ізохорно-ізотермний потенціал зменшується, досягаючи мінімуму у стані рівноваги. Таким чином, у стані рівноваги:

F = F_min; dF = 0; d²F > 0 (мінімум F). (7.31)

Таким чином, самочинні процеси, які відбуваються при умовах V, T=const, можливі лише у напрямку зменшення F і їх границею, тобто умовою рівноваги, є досягнення мінімального значення F (рис. 7.2). При цих же умовах можливі процеси при dF > 0, але вони є несамочинними і вимагають витрат енергії.

На підставі (7.26) запишемо при T = const:

ΔF = ΔU – TΔS, тобто ΔU= ΔF+ TΔS, (7.32)

де ΔU – ізохорний тепловий ефект;

ТΔS – ентропійний фактор.

На підставі рівняння (7.29) для рівновагових процесів запишемо:

– SdT – pdV = dF, (7.33)

звідки

· при V=const 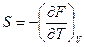; (7.34)

· при Т=const 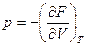. (7.35)

Дата добавления: 2014-12-25