Метод итераций. Преобразуем уравнение (2.1) к эквивалентному виду

Преобразуем уравнение (2.1) к эквивалентному виду

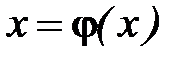. (2.15)

Выбрав в качестве начального приближения точку 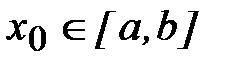, построим последовательность

(2.16)

Докажем, что эта последовательность при любом 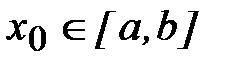сходится к единственному на отрезке [a, b] корню уравнения (2.1), если:

1) функция 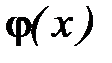определена и дифференцируема на отрезке

[a, b];

2) все ее значения принадлежат этому отрезку при ;

3) существует такое число 0<q<1, что 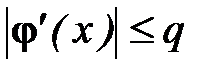при .

Рассмотрим ряд

(2.17)

где x_n определено формулой (2.16). Частичная сумма этого ряда

.

Оценим по модулю каждый член ряда

,

где точка a - расположена между x_i-1 и x_i.

Имеем:

Следовательно, ряд (2.17) сходится абсолютно, т.е. существует

,

откуда следует сходимость последовательности (2.16)

.

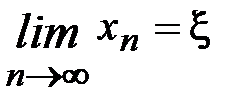Перейдем к пределу в равенстве (2.16):

,

т.е. x - является корнем уравнения (2.15) и эквивалентного ему уравнения (2.1). Докажем единственность x. Пусть существуют два корня уравнения (2.15):

где точка a расположена между x и x₁, т.е. 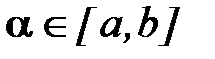Преобразуем это равенство

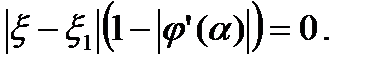
Но 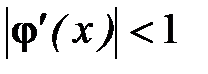на [a, b], значит,

.

Оценим абсолютную погрешность приближения 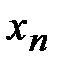, полученного методом итераций

Укажем теперь достаточно общий прием построения функции 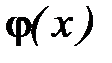, для которой будет обеспечено выполнение условий сходимости итерационного процесса (2.16). Пусть на отрезке [a, b] существует f’(x) и сохраняет знак так, что

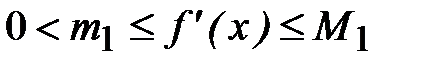
(мы приняли здесь, что 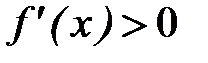, в противном случае рассматривается функция – f(x)). Умножив уравнение (2.1) на число l и вычтя результат из тождества , получим

.

Выберем l так, чтобы

.

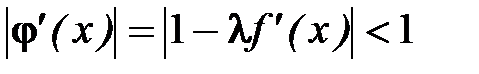Отсюда

.

Из правого неравенства получим l > 0, а из левого

.

Обычно полагают . Тогда

.

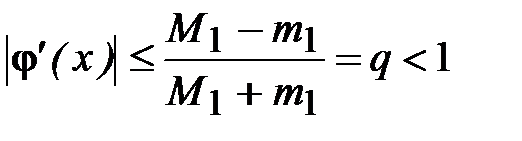Тренировочные задания.

I. Методом хорд вычислить наибольший корень уравнения 2х³ + 3х² – 7х + 1 = 0 с точностью до двух верных знаков в узком смысле. Предварительно провести отделение корней данного уравнения.

II. Вычислить методом касательных корень уравнения 2х³ + 3х² – 7х + 1 = 0, расположенный на отрезке [0; 1] с точностью до 0,005.

III. Методом итераций вычислить отрицательный корень уравнения 2х³ + 3х² – 7х + 1 = 0 с точностью до ε = 0,05.

Дата добавления: 2014-12-25