З.2. Метод прогонки

Метод прогонки применяется для решения систем специального вида, матрица которых является трехдиагональной:

(3.7)

Такие системы обычно возникают при численном решении краевых задач для дифференциальных уравнений, интерполировании сплайнами и моделировании некоторых процессов.

Выразим из первого уравнения системы (3.7) переменную x₀, а из последнего - переменную x_n, предполагая, что 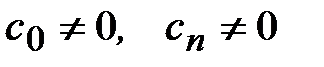, и запишем эту систему в следующем виде:

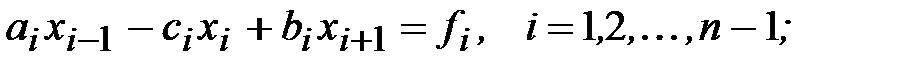(3.8)

(3.9)

Уравнения (3.8) в совокупности обычно называются разностным уравнением второго порядка или точечным разностным уравнением, а уравнения (3.9) - краевыми условиями для разностного уравнения (З.8). Система же (3.8)-(3.9) в целом называется разностной краевой задачей.

Выведем расчетные формулы метода прогонки для решения системы (3.8)-(3.9). Подставим первое краевое условие в первое уравнение (3.8). Получим уравнение

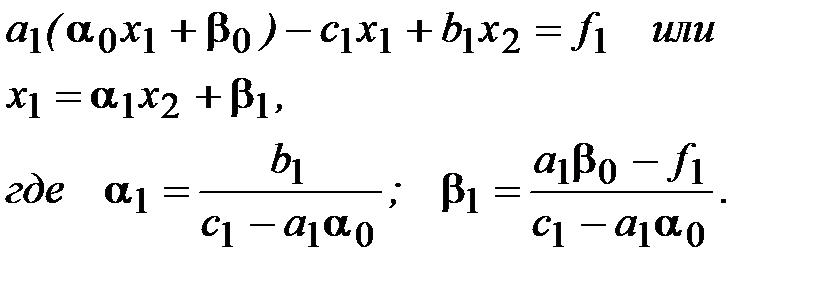(3.10)

Найденное выражение (3.10) для x₁ подставим в следующее уравнение (3.8) и получим уравнение, связывающее переменные x₂ и x₃ и т.д.

Допустим, что уже найдено соотношение

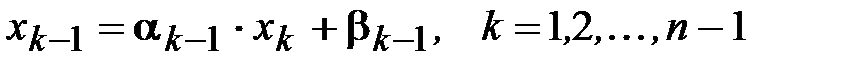. (3.11)

Подставим (3.11) в k -е уравнение (3.8)

Разрешим это уравнение относительно x _k:

, (3.12)

(3.13)

Таким образом, коэффициенты уравнений (3.12), связывающие соседние переменные , 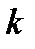= 1,2,...,п-1, можно определить из рекуррентных соотношений (3.13), поскольку заданы в (3.9).

Подставив во второе краевое условие (3.9) выражение для x_n-1, вытекающее из формулы (3.12) при 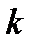= п-1, получим

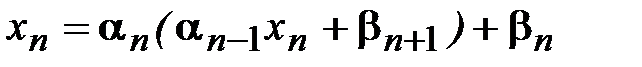, (3.14)

где - заданные в (3.9) коэффициенты, а вычислены по формулам (3.13). Из уравнения (3.14) вычисляем x_n:

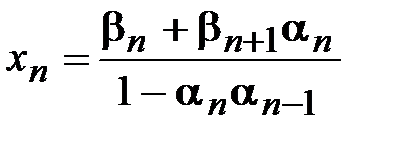. (3.15)

Затем по формуле (3.12) в обратном порядке вычисляем остальные неизвестные 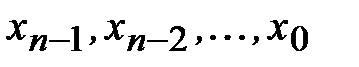. Формула (3.12) при = 0 совпадает с первым краевым условием (3.9).

Процесс вычисления коэффициентов 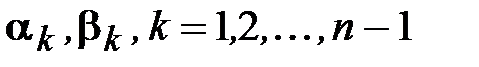по формулам (3.13) называется прямой прогонкой, а вычисление неизвестных по формулам (3.15), (3.12) - обратной прогонкой.

Метод прогонки можно применять, если знаменатели формул (3.15), (3.12) не обращаются в нуль. Докажем, что для возможности применения метода прогонки достаточно потребовать, чтобы коэффициенты системы (3.8)-(3.9) удовлетворяли условиям

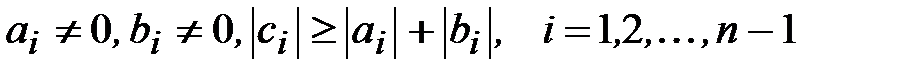, (3.16)

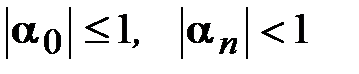. (3.17)

Сначала докажем индукцией, что при условиях (3.16), (3.17)

.

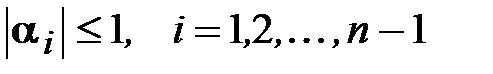По первому условию (3.17)

.

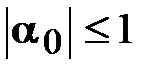Предположим, что все

,

и докажем, что

.

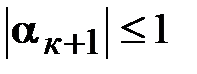Из оценок

и условий (3.16) получаем

,

т.е. знаменатели выражений (3.13) не обращаются в нуль. Кроме того,

,

Следовательно,

.

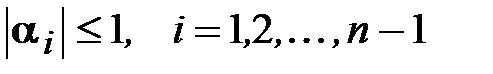Далее, учитывая второе из условий (3.17) и только что доказанное неравенство 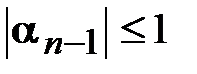, имеем

,

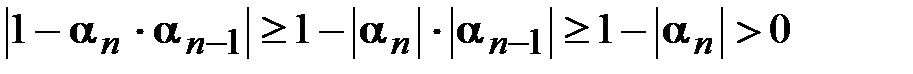т.е. не обращается в нуль и знаменатель в выражении для х_п.

К аналогичному выводу можно прийти и в том случае, когда условия (3.16), (3.17) заменяются условиями

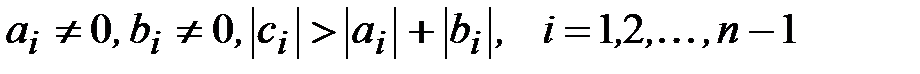, (3.18)

(3.19)

или условиями

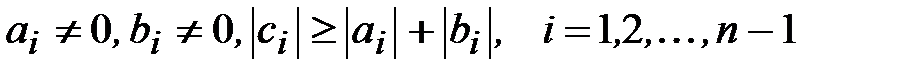, (3.20)

. (3.21)

При условиях (3.18), (3.19) из предположения следует

.

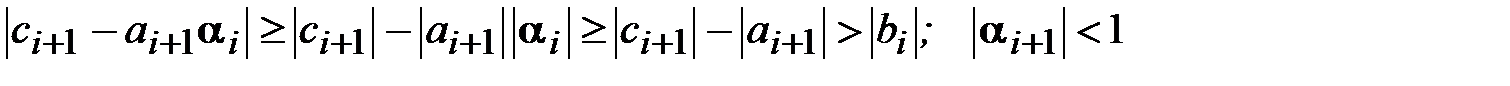Т.е. все прогоночные коэффициенты, начиная с первого, по модулю строго меньше единицы. При этом

.

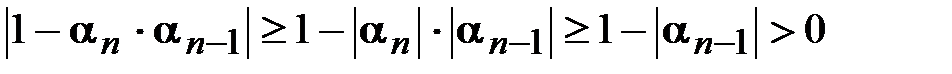При условиях (3.20), (3.21) из предположения 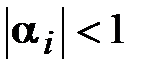следует

Таким образом, при выполнении условий (3.16), (3.17) (так же как и условий (3.18), (3.19) или условий (3.20), (3.21)) система (3.8)-(3.9) эквивалентна системе (3.12), (3.15), т.е. эти условия гарантируют существование и единственность решения системы (3.8)-(3.9) и возможность нахождения этого решения методом прогонки. Кроме того, доказанные неравенства 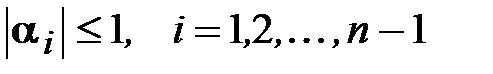обеспечивают устойчивость счета по рекуррентным формулам (3.12). Последнее означает, что погрешность, внесенная на каком - либо шаге вычислений, не будет возрастать при переходе к следующим шагам. Действительно, пусть в формуле (3.12) при вместо вычислена величина .

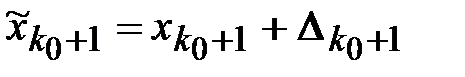Тогда на следующем шаге вычислений, т.е. при , вместо 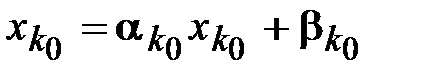получим величину 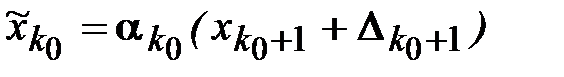и погрешность окажется равной .

Отсюда получим, что

,

т.е. погрешность не возрастает.

Дата добавления: 2014-12-25