
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частичная проблема собственных значений
|
|
|
|
Задача определения собственных значений и собственных векторов важна и как самостоятельная задача, и как вспомогательная задача. Её можно разбить на три естественных этапа:
построение характеристического многочлена
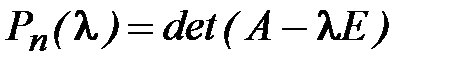 ;
;
решение алгебраического уравнения 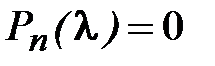 ,
,
т.е. отыскание собственных значений 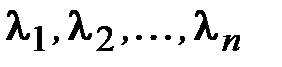 матрицы;
матрицы;
отыскание ненулевых решений однородной системы
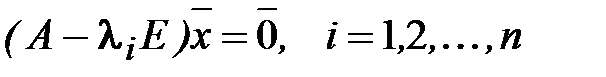 ,
,
т.е. нахождение собственных векторов матрицы А. Каждый из трех отмеченных этапов представляет собой достаточно сложную задачу. Однако иногда можно вычислить собственные значения и соответствующие им собственные векторы, минуя этап построения характеристического многочлена и не прибегая к решению указанных выше систем однородных алгебраических уравнений. Этого удается достичь при помощи различных косвенных соображений, используя те или иные свойства собственных значений и собственных векторов матрицы.
Мы рассмотрим приближенный метод решения частичной проблемы собственных значений, т.е. задачи нахождения не всех собственных значений и соответствующих им собственных векторов матрицы, а только некоторых из них - метод отыскания максимального по модулю собственного значения матрицы.
Предположим, что квадратная матрица А порядка п, имеет п собственных линейно независимых нормированных векторов, т.е. эти векторы образуют базис п -мерного векторного пространства (как известно, это всегда имеет место, если А - симметрическая матрица).
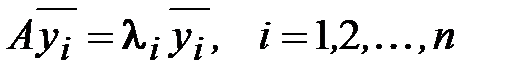 . (3.46)
. (3.46)
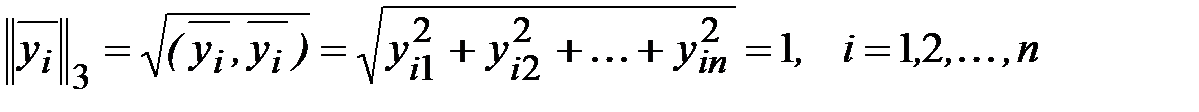 . (3.47)
. (3.47)
Допустим, что
 . (3.48)
. (3.48)
Возьмем произвольный вектор  . Имеем
. Имеем
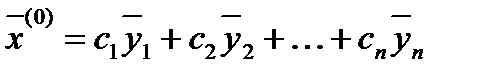 ,
,
где  - координаты вектора
- координаты вектора  в базисе собственных векторов
в базисе собственных векторов 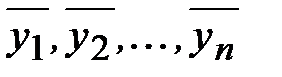 . Предположим, что
. Предположим, что
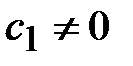 . (3.49)
. (3.49)
Последовательно находим векторы
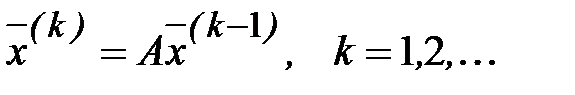 (3.50)
(3.50)
Тогда согласно (3.46)
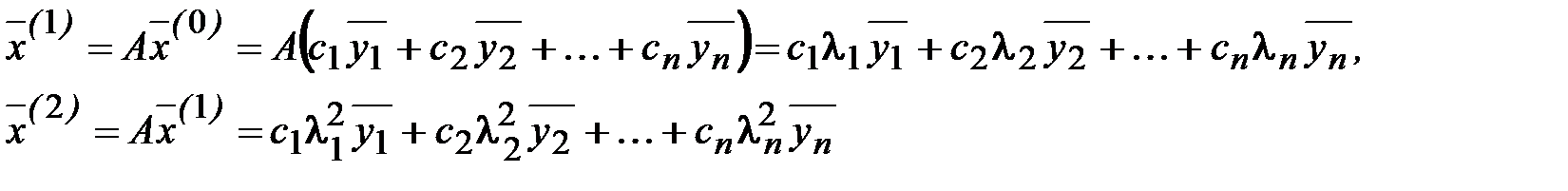
и вообще
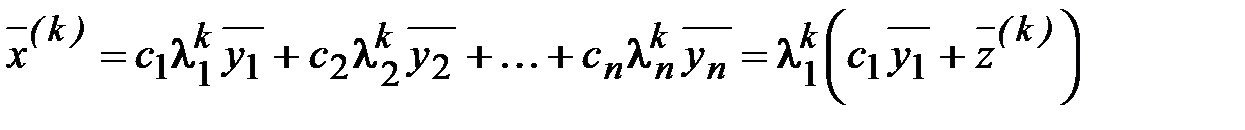 , (3.51)
, (3.51)
где 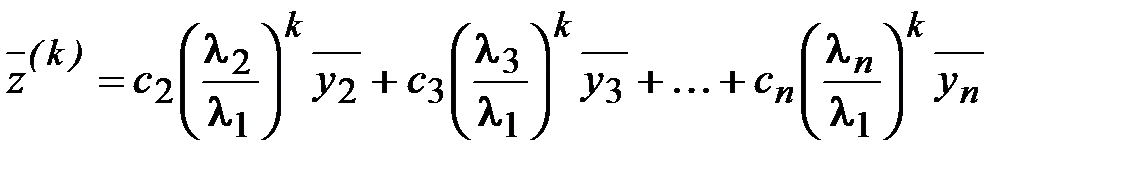 .
.
В силу (3.48) 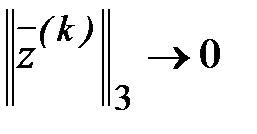 при
при 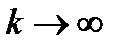 и
и
 . (3.52)
. (3.52)
Значит, вектор  при больших
при больших 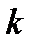 близок к собственному вектору матрицы А, соответствующему собственному значению
близок к собственному вектору матрицы А, соответствующему собственному значению 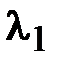 .
.
Используя (3.51), найдем скалярное произведение
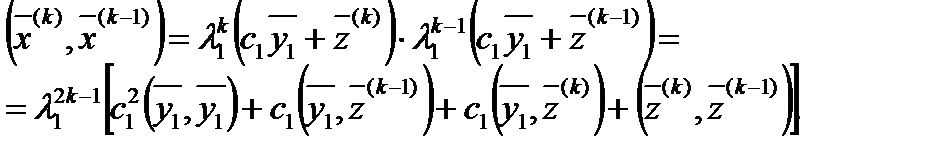 (3.53)
(3.53)
Согласно (3.47) 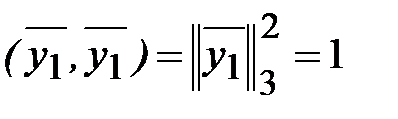 . Для каждого из остальных скалярных произведений в (3.53) воспользуемся неравенством Коши - Буняковского (3.25):
. Для каждого из остальных скалярных произведений в (3.53) воспользуемся неравенством Коши - Буняковского (3.25):

Теперь из (3.53) с учётом (3.52) получим
 .
.
Аналогично можем получить
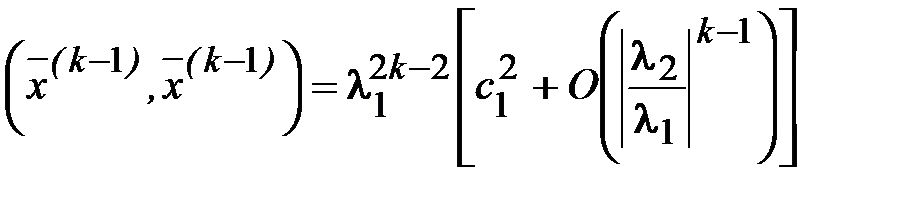 .
.
Последние две соотношения дадут
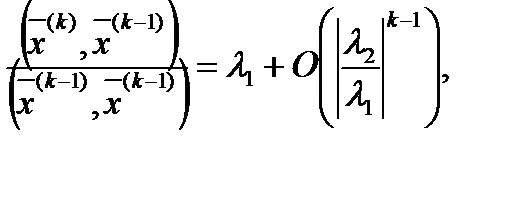
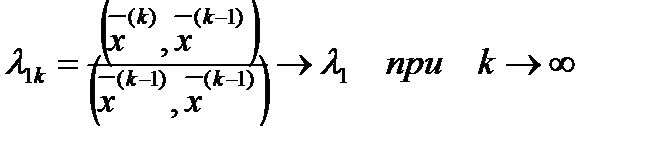 . (3.54)
. (3.54)
Таким образом, при условии (3.48) итерационный процесс (3.50) позволяет найти с любой точностью максимальное по модулю собственное значение 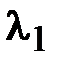 и соответствующий ему собственный вектор.
и соответствующий ему собственный вектор.
Следует заметить, что если 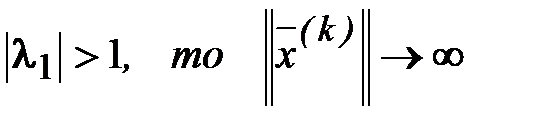
 . Если же
. Если же 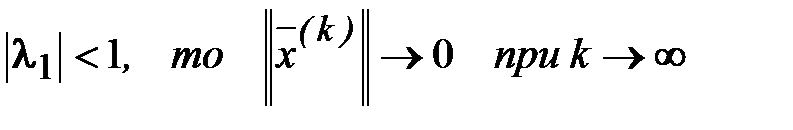 . То и другое явление при счете на ЭВМ нежелательно. В первом случае может наступить переполнение (выход за допустимый диапазон чисел). Во втором случае
. То и другое явление при счете на ЭВМ нежелательно. В первом случае может наступить переполнение (выход за допустимый диапазон чисел). Во втором случае  может стать машинным нулем (слишком малой величиной), и информация теряется. Поэтому целесообразно на каждой итерации нормировать собственный вектор
может стать машинным нулем (слишком малой величиной), и информация теряется. Поэтому целесообразно на каждой итерации нормировать собственный вектор 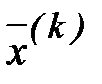 , т.е. итерации вести по формулам:
, т.е. итерации вести по формулам:
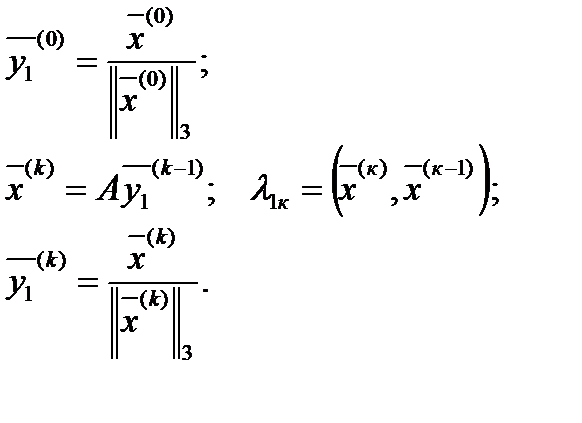
Подтверждением того, что 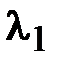 не является кратным собственным значением и что нет собственного значения, равного -
не является кратным собственным значением и что нет собственного значения, равного - 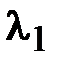 , служит сходимость итерационного процесса при выборе различных
, служит сходимость итерационного процесса при выборе различных  к одному и тому же собственному вектору (с точностью до противоположного вектора).
к одному и тому же собственному вектору (с точностью до противоположного вектора).
Рассмотрим теперь, как, используя метод отыскания максимального по модулю собственного значения матрицы, определить максимальное и минимальное собственные значения симметрической матрицы. Как известно, все собственные значения вещественной симметрической матрицы А действительны [8, II] и существует ортонормированный базис 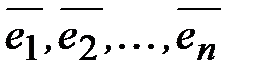 , составленный из собственных векторов матрицы А.
, составленный из собственных векторов матрицы А.
Пусть  -
-
некоторый алгебраический многочлен от t первой степени с действительными коэффициентами. Обозначим через В следующую матрицу
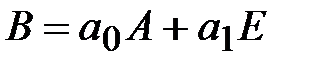 ,
,
где Е - единичная матрица. Докажем, что собственные значения матриц А и В связаны соотношением
 , (3.55)
, (3.55)
а собственный вектор матрицы А, соответствующий собственному значению 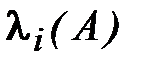 , является собственным вектором матрицы В, соответствующим собственному значению
, является собственным вектором матрицы В, соответствующим собственному значению 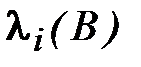 .
.
Пусть 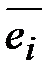 - собственный вектор матрицы А, соответствующий собственному значению
- собственный вектор матрицы А, соответствующий собственному значению 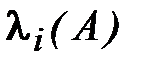 :
:
 .
.
Тогда
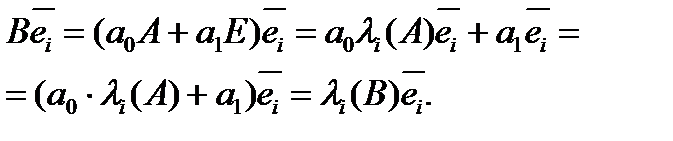
Допустим, что максимальное по модулю собственное значение  симметрической матрицы А известно. Постоим матрицу
симметрической матрицы А известно. Постоим матрицу
 (3.56)
(3.56)
и определим для нее максимальное по модулю собственное значение 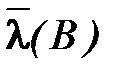 .
.
Если 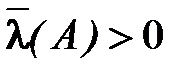 , то очевидно, что
, то очевидно, что
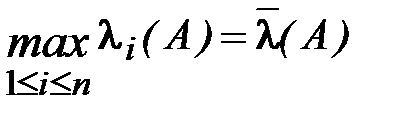 .
.
Кроме того, согласно (3.55) и (3.56)
 .
.
Поэтому
 ,
,
т.е.  . (3.57)
. (3.57)
Если 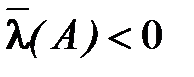 , то
, то

и
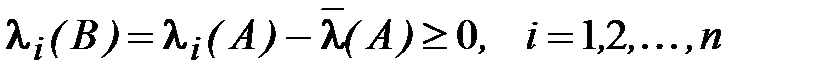 .
.
Поэтому
 ,
,
откуда
 .
.
Тренировочные задания.
Задание I.
Решить систему с точностью до 0,001.
| 4,5x1–1,8x2+3,6x3=–1,7; | (I) |
| 3,1x1+2,3x2–1,2x3=3,6; | (II) |
| 1,8x1+2,5x2+4,6x3=2,2. | (III) |
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 1490; Нарушение авторских прав?; Мы поможем в написании вашей работы!