Погрешность арифметических действий

1. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Действительно, если

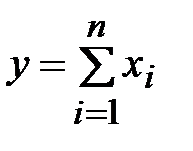(1.22)

то на основании общей формулы теории погрешностей (1.20)

.

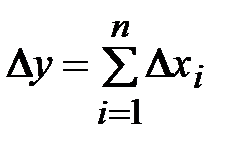Из полученной формулы следует: абсолютная погрешность алгебраической суммы не может быть меньше абсолютной погрешности наименее точного из слагаемых, так как увеличение точности за счет остальных слагаемых невозможно. Поэтому, чтобы не производить лишних вычислений, не следует сохранять лишние знаки и в более точных слагаемых.

Пример 9. Найти сумму приближенных чисел

у = 5,8 + 287,649 + 0,008064

и оценить погрешность результата, считая все знаки слагаемых верными в узком смысле.

Решение. Вычислим указанную сумму тремя способами

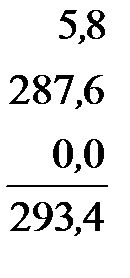
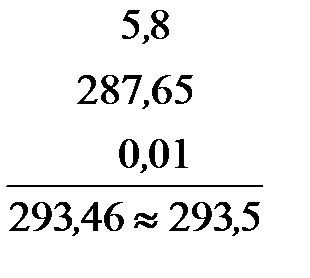
Очевидно, что только последний из приведенных способов сложения будет правильным, так как в числе 5,8 отброшенные знаки неизвестны, поэтому нет смысла получать результат с точностью до миллионных, которая ничем не гарантирована.

Второй способ также не верен, так как не использует большую точность двух других слагаемых. Поэтому будет правильным сохранить в остальных слагаемых один лишний десятичный знак, а после сложения результат округлить до десятых согласно с точностью числа, имеющего наибольшую абсолютную погрешность. При большом числе слагаемых вычисления лучше вести с двумя запасными десятичными знаками.

Погрешность полученной суммы будет равна сумме трех слагаемых:

1) сумма погрешностей исходных данных

;

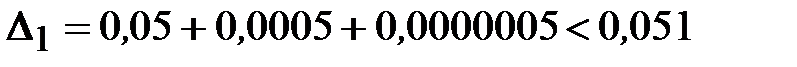2) абсолютная величина суммы ошибок округления слагаемых

;

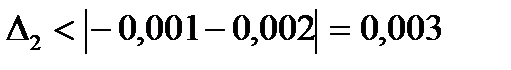3) погрешность округления результата

.

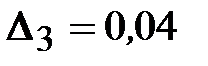Следовательно,

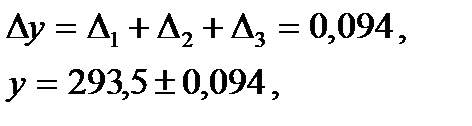
т.е. у имеет 4 верных знака в широком смысле и 3 в узком.

2. Относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

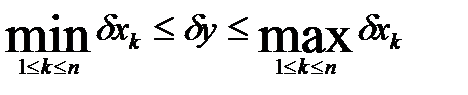. (1.23)

Действительно, если

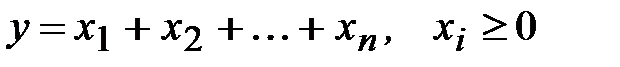, (1.24)

то

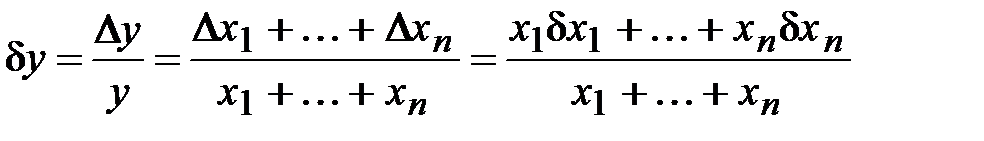. (1.25)

Обозначив

, (1.26)

получим

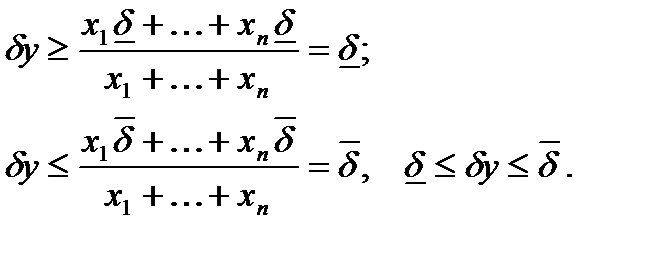(1.27)

3. Относительная погрешность разности двух положительных чисел больше относительных погрешностей этих чисел, особенно, если эти числа близки между собой. Это приводит к потере точности при вычитании близких чисел, что следует учитывать при выборе вычислительной схемы.

Действительно, если

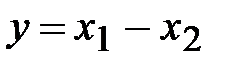, (1.28)

то

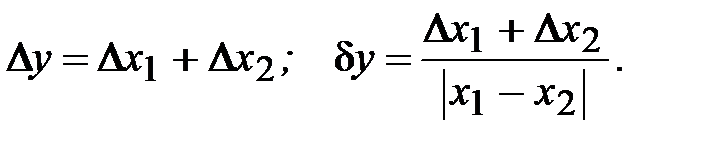(1.29)

Пример 10. Найти разность двух чисел 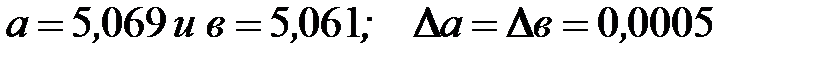. Оценить погрешность результата.

Решение.

.

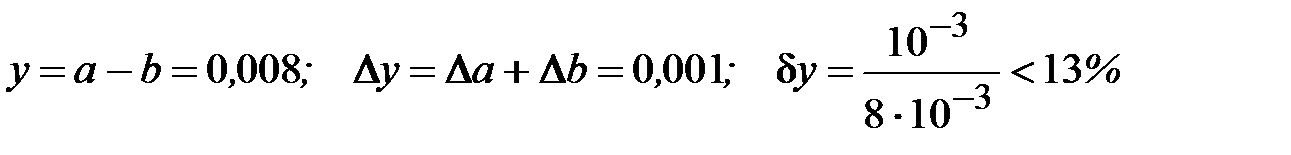Таким образом, результат имеет один верный знак в широком смысле, хотя сами числа имеют по четыре верных знака. Относительная погрешность разности у более чем в тысячу раз больше относительной погрешности самих чисел .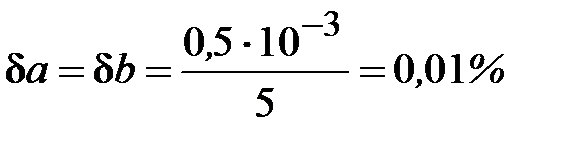

4. При умножении и делении приближенных чисел складываются их относительные погрешности.

Действительно, если

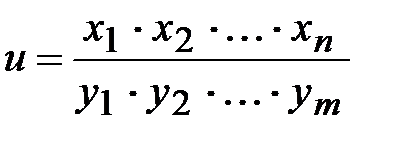, (1.30)

то

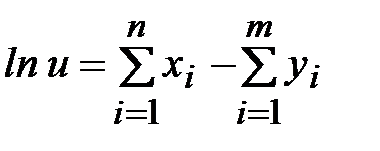
и на основании этого выражения получаем

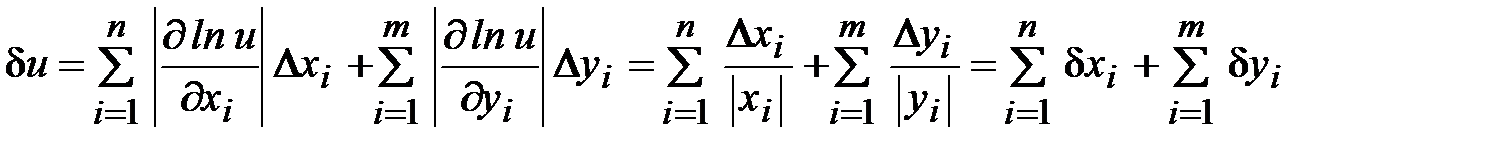(1.31)

Из полученного выражения видно, что относительная погрешность произведения и частного не может быть меньше, чем относительная погрешность наименее точного из сомножителей, следовательно, число верных знаков произведения не может быть больше наименьшего числа верных знаков сомножителей. Поэтому при перемножении нескольких чисел, имеющих разное число верных значащих цифр, выполняют следующие правила:

1) выделяют число, имеющее наименьшее число верных значащих цифр;

2) округляют оставшиеся сомножители, оставляя в них на одну значащую цифру больше, чем в выделенном сомножителе;

3) сохраняют в произведении столько значащих цифр, сколько верных значащих цифр имеет выделенный сомножитель.

§1.7. Обратная задача теории погрешностей

Основная задача теории погрешностей заключалась в том, что по известным погрешностям аргументов находилась погрешность функции. На практике очень важное значение имеет и обратная задача: каковы должны быть погрешности аргументов, чтобы абсолютная погрешность функции не превышала заданной величины?

На основании общей формулы теории погрешностей имеем

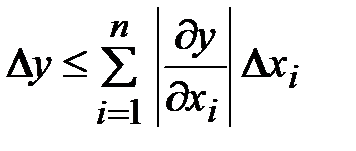. (1.32)

Задача отыскания допустимых значений абсолютной погрешности аргументов по известной абсолютной погрешности функции является математически неопределенной, так как в общем случае для определения п неизвестных 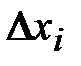мы имеем одно уравнение.

Обратная задача теории погрешностей имеет однозначное решение только для функции одного аргумента. Действительно, на основании общей формулы теории погрешностей

,

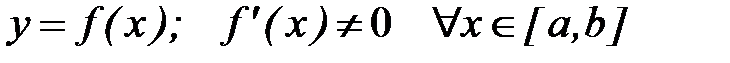следовательно,

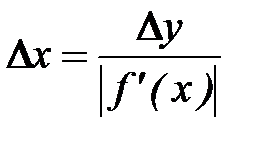. (1.33)

1. Принцип равных влиянии. Согласно этому принципу предполагается, что все выражения

,

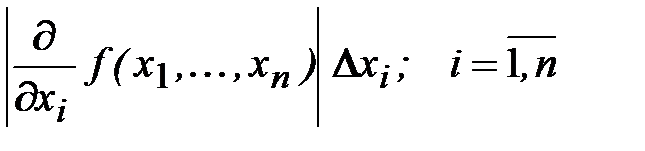одинаково влияют на образование общей абсолютной погрешности, т.е.

.

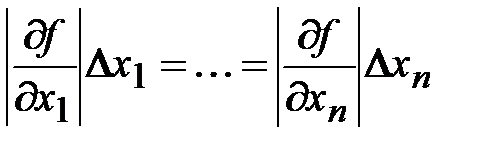Пусть нам задана абсолютная погрешность 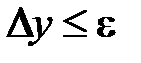. На основании общей формулы теории погрешностей можно написать

.

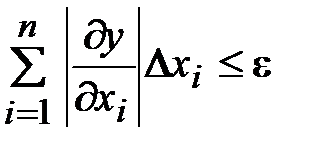Тогда

,

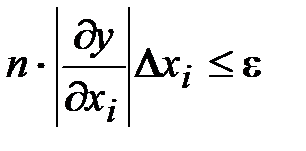откуда

.

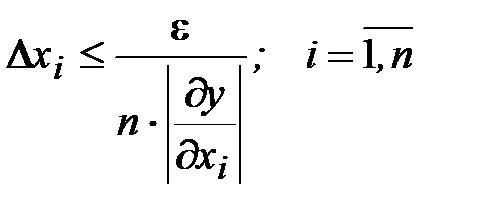2. Принцип равных абсолютных погрешностей. Согласно этому принципу предполагается, что

Dx₁=Dx₂ =…=Dx_n.

Тогда из общей формулы теории погрешностей будем иметь

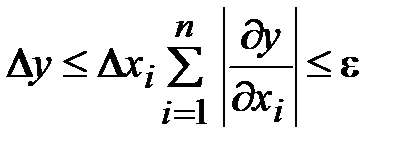
или

.

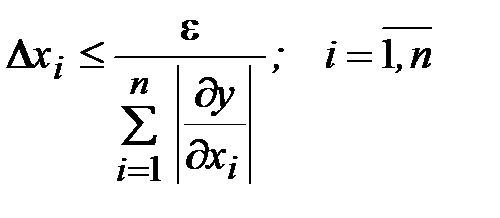3. Принцип равных относительных погрешностей. Согласно этому принципу предполагается, что

.

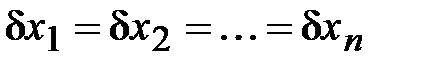По определению 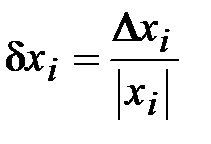, тогда .

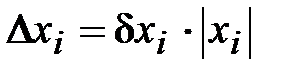Подставляя это выражение в общую формулу, получим

,

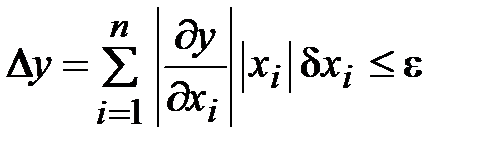откуда

.

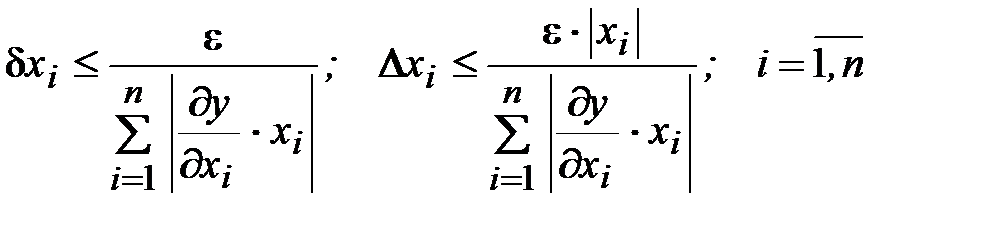Тренировочные задания.

Задание I.

1. Дано приближенное число 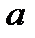= 88,325 и известно, что у этого числа три верных значащих цифры в широком(узком) смысле. Оценить абсолютную и относительную погрешность в обоих случаях.

2. Дано приближенное число 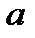= 2,7182 и его абсолютная погрешность D= 0,007. Определить, какие значащие цифры приближенного числа будут верными в широком(узком) смысле.

3. Дано приближенное число 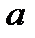= 2,7182 и его относительная погрешность d 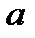= 1%. Определить, какие значащие цифры приближенного числа будут верными в широком(узком) смысле.

Задание II.

1. Со сколькими верными знаками в широком(узком) смысле следует вычислить 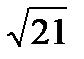= 4,…, чтобы

а) абсолютная погрешность не превышала ξ = 0,007;

б) относительная погрешность не превышала 1%.

2. Вычислить значение 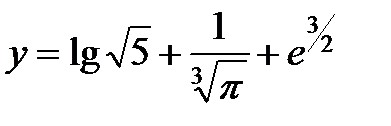и оценить абсолютную погрешность результата, взяв приближенные значения аргументов с четырьмя верными знаками.

3. С каким числом верных знаков следует взять значения аргументов функции 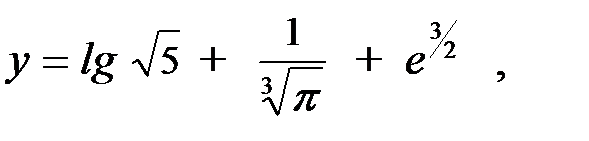чтобы вычисленное значение этой функции имело 4 верных знака?

Задание III.

1. Вычислить значение функции 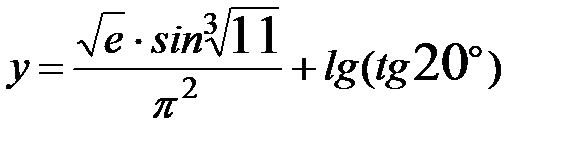и оценить абсолютную погрешность результата, взяв значения аргументов с четырьмя верными знаками.

2. С каким числом верных знаков следует взять значения аргументов функции 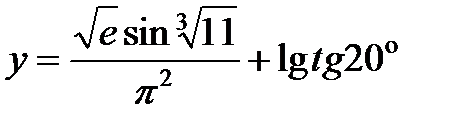, чтобы вычисленное значение функции имелo три верных знака?

Дата добавления: 2014-12-25