Число верных знаков приближенного числа. Связь абсолютной и относительной погрешности с числом верных знаков. Правила подсчета числа верных знаков

Всякое положительное десятичное число а может быть единственным образом представлено в виде конечной или бесконечной десятичной дроби:

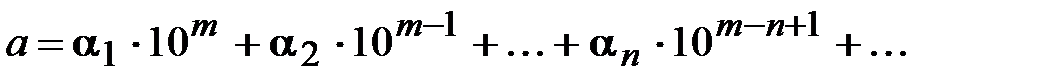(1.5)

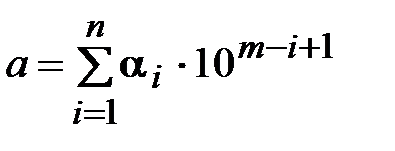или (1.6)

где 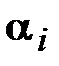- десятичные цифры (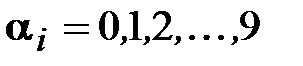), причем 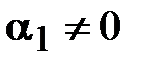, т – некоторое число (старший разряд числа а). Например, в десятичной системе счисления:

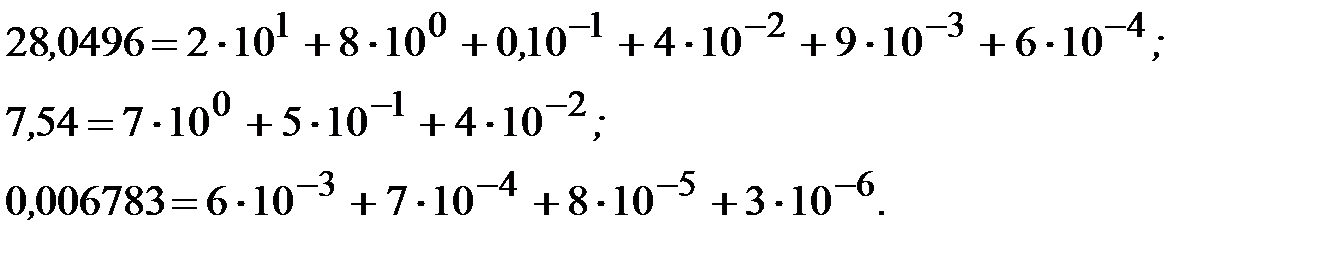
Определение 4. Значащими цифрами числа а называют все цифры в его записи (1.5) начиная с первой слева, отличной от нуля. Например, приводимые ниже числа имеют следующее количество значащих цифр:

5423,47 6 значащих цифр,

0,0000605 3 значащие цифры,

0,060500 5 значащих цифр.

Как видно из приведенных примеров, цифра 0 имеет особое значение при определении числа значащих цифр. Например, в числе 0,00710300 первые три нуля не являются значащими цифрами и служат только для установления старшего десятичного разряда числа. Остальные три являются значащими цифрами, так как первый из них находится между значащими цифрами, а второй и третий, как отражено в записи, указывают, что в приближенном числе сохранены десятичные разряда 10^-7 и 10^-8. Если же в данном числе 0,00710300 последние две цифры не являются значащими цифрами, то это число лучше записать в виде 0,007103. Числа 0,00710300 и 0,007103 не равноценны, так как первое из них имеет 6 значащих цифр, а второе – только 4 значащих цифры. Цифра 0, стоящая в конце числа, может иметь двоякий смысл, как это видно из следующих утверждений:

а) 1 кг = 1000 г;

б) население США по одной из переписей составляло 195530000 человек

В первом случае имеем точное соотношение, поэтому все нули здесь – значащие цифры. Во втором случае нули стоят вместо неизвестных цифр, и число имеет только 5 значащих цифр. Для того чтобы избежать недоразумения, никогда не следует писать нули вместо неизвестных цифр, а лучше применять такую форму записи:

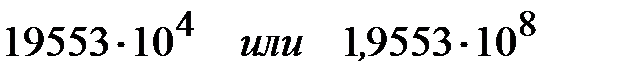
Пример 5. Пусть в результате измерения получено число, имеющее две значащие цифры, l = 72 мм. Если этот результат, не измеряя отрезок с большей точностью, выразить в метрах, километрах или микронах и написать, что l =0,072 м, или l =0,000072 км, или l =72000 мкм, то нули ни в первом, ни во втором, ни в третьем случаях не будут значащими. В дальнейшем условимся различать такие числа, как 7,2; 7,20; 7,200.

Все они выражают одно и то же числовое значение некоторой величины, но определены с разным количеством значащих цифр.

Точность приближенного числа зависит не от количества значащих цифр, а от количества верных значащих цифр. Различают значащие цифры верные в узком и широком смыслах.

Определение 5. Цифры 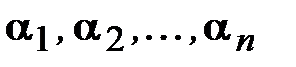приближенного числа а называют верными в узком смысле, если абсолютная погрешность 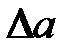приближенного числа а не превосходит половины единицы (т-п+1) – го разряда, которому принадлежит цифра 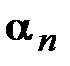, т.е. если

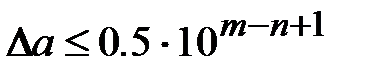. (1.7)

Пример 6. Оценить абсолютную погрешность приближенного числа а = 4,483, если известно, что оно имеет 3 верных знака в узком смысле.

Решение. По определению 5

.

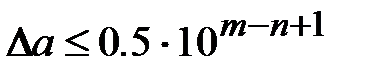В нашем случае старший разряд числа равен 10⁰, т.е. т = 0, а п = 3. Поэтому получаем

.

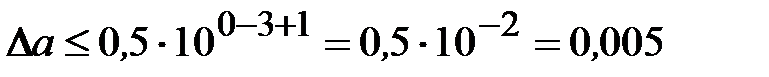В математических таблицах все числа определены до верных значащих цифр в узком смысле. Так, например, в четырехзначных таблицах Брадиса В.М. гарантировано, что абсолютная погрешность квадратных корней не превосходит 0,5*10^-3 (так как там приведены квадратные корни чисел от 1 до 100). В некоторых случаях, например при получении числа путем измерения, удобнее говорить о числе верных знаков в широком смысле.

Определение 6. Цифры 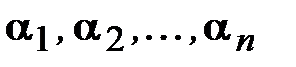приближенного числа а называют верными в широком смысле, если абсолютная погрешность 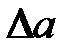приближенного числа а не превосходит единицы (т-п+1) – го разряда, которому принадлежит цифра 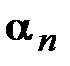, т.е. если

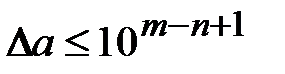. (1.8)

Например, если число а = 4,483 имеет п = 3 верных знака в широком смысле, то его абсолютная погрешность не превосходит

.

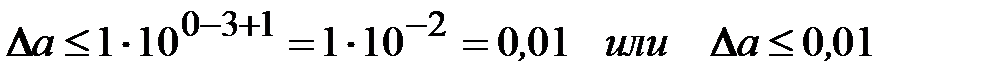Определения 5 и 6 можно обобщить.

Определение 7. Цифры 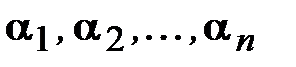приближенного числа а называются верными в смысле w, если абсолютная погрешность числа а не превосходит величины 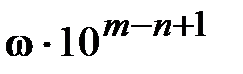, т.е.

. (1.9)

Определение числа верных значащих цифр позволяет решать и обратную задачу, т.е. определять, какие знаки в приближенном числе верные, а какие нет, если известна его абсолютная погрешность.

Пример 7. Определить, какие значащие цифры приближенного числа а = 2,4483 будут верными в узком (широком) смысле, если его абсолютная погрешность равна .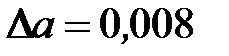

Решение. Следуя определению числа верных значащих цифр, для того чтобы 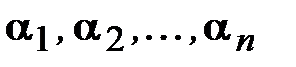были верными значащими цифрами числа а, необходимо потребовать выполнения неравенства:

, где ,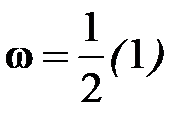

которое в нашем примере имеет вид

.

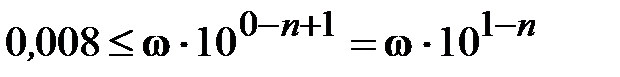Решая неравенство при 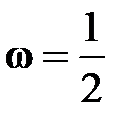, получим

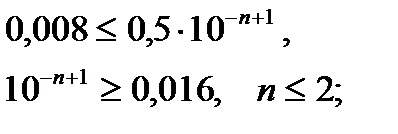
а при w = 1 получим

.

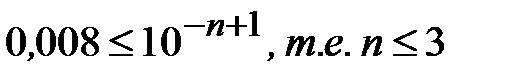Таким образом, у числа а = 2,4483 три верные цифры в широком смысле и две – в узком. Остальные цифры приближенного числа 2,4483 не верны.

Приведенный способ определения числа верных значащих цифр по известной абсолютной погрешности, связанный с решением неравенства, можно заменить более простым правилом: число верных знаков в приближенном числе отсчитывается, начиная с первой значащей цифры числа до первой значащей цифры его абсолютной погрешности.

Пример 8. Определить количество верных значащих цифр в узком и широком смысле для числа а = 0,0076539, если .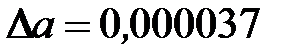

Решение. Напишем абсолютную погрешность над числом

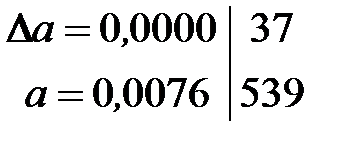
Очевидно, что все значащие цифры, стоящие слева перед вертикальной чертой, проведенной перед первой значащей цифрой погрешности, будут всегда верными в широком смысле, так как число, стоящее за вертикальной чертой (в погрешности), всегда меньше единицы разряда, стоящего слева от черты, в данном случае

0,000037<0,0001

В нашем случае значащие цифры 7 и 6, стоящие слева от черты, будут верными и в узком смысле, так как величина погрешности 0.000037<0.00005 -половины единицы разряда десятитысячных, которому принадлежит последняя цифра 6. Если же для числа а = 0,0076539 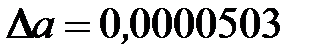, то по этому же правилу

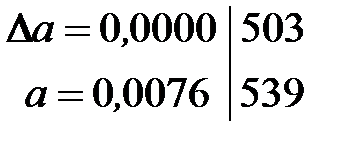
число будет иметь две значащие цифры в широком смысле слова и только одну в узком, так как

.

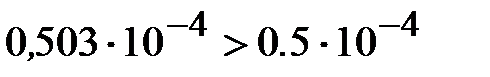На основании обобщенного определения абсолютная погрешность приближенного числа а связана с числом верных знаков соотношением (1.9)

.

В какой же зависимости от числа верных значащих цифр находится относительная погрешность?

Пусть приближенное число а,

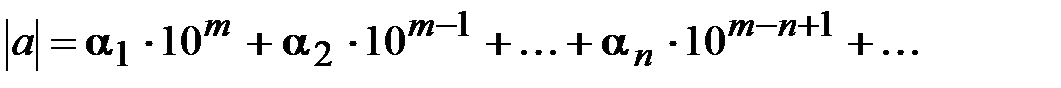(1.10)

имеет п верных значащих цифр в смысле определения 7.

Разделив обе части неравенства (1.9) на выражение (1.10), получим

,

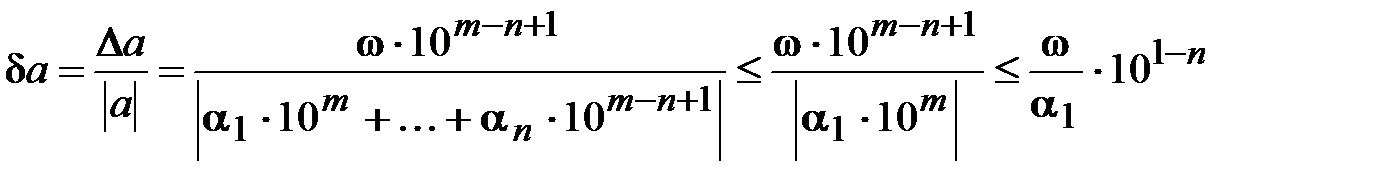т.е.

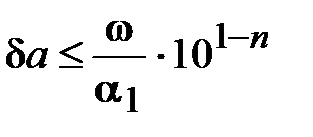, (1.11)

где 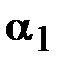- первая значащая цифра числа, п – количество верных значащих цифр.

§1.5. Общая формула теории погрешностей
(погрешность вычисления значения функции)

Основная задача теории погрешностей заключается в следующем: известны погрешности некоторой системы величин, требуется определить погрешность данной функции от этих величин.

Пусть в некоторой области 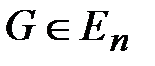задана дифференцируемая функция

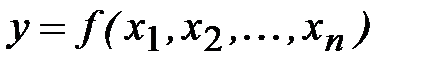(1.12)

и известны абсолютные погрешности аргументов

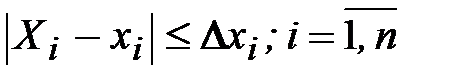. (1.13)

Обозначим через

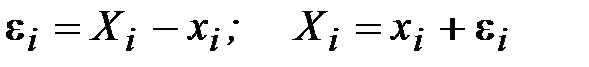, (1.14)

тогда

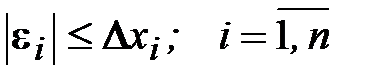. (1.15)

Абсолютная погрешность функции выражается следующим образом:

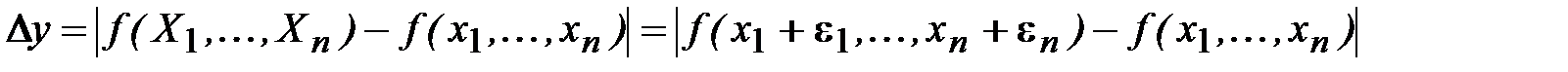. (1.16)

Согласно формуле Лагранжа

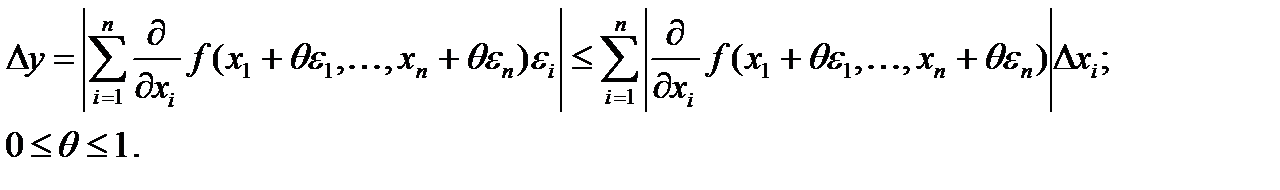(1.17)

Отсюда

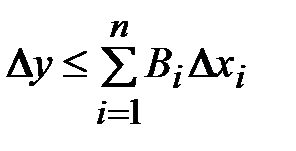, (1.18)

где

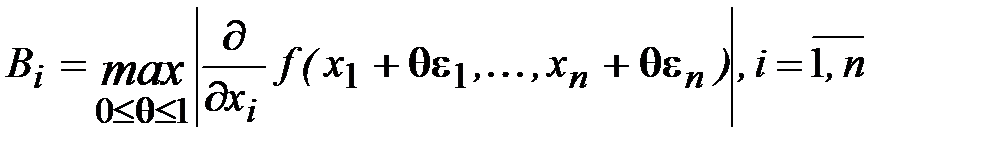. (1.19)

Когда погрешности аргументов 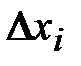малы, величины B_i допустимо заменить на абсолютные значения частных производных функции 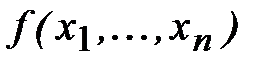в точке .

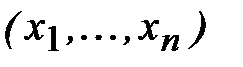С учетом этого для абсолютной погрешности функции получится

приближенное, но более простое выражение

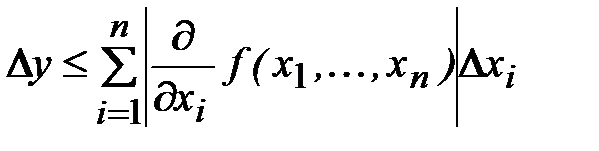. (1.20)

Данное выражение для определения абсолютной погрешности функции носит название общей (или основной) формулы теории погрешностей.

Разделив обе части выражения (1.20) на 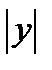, получим выражение для относительной погрешности функции:

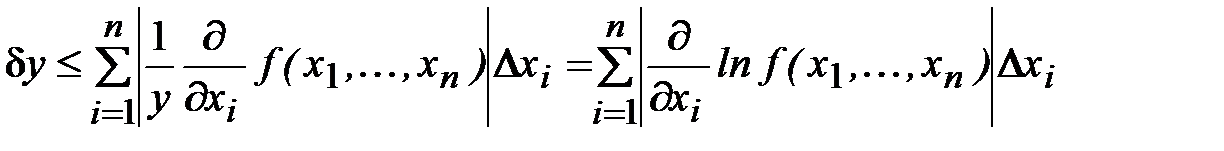. (1.21)

В случае функции одного аргумента выражения для погрешностей функции упрощаются. Действительно, если

,

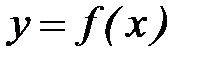то

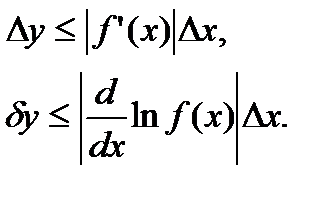
В частности, для основных элементарных функций получаем следующие правила:

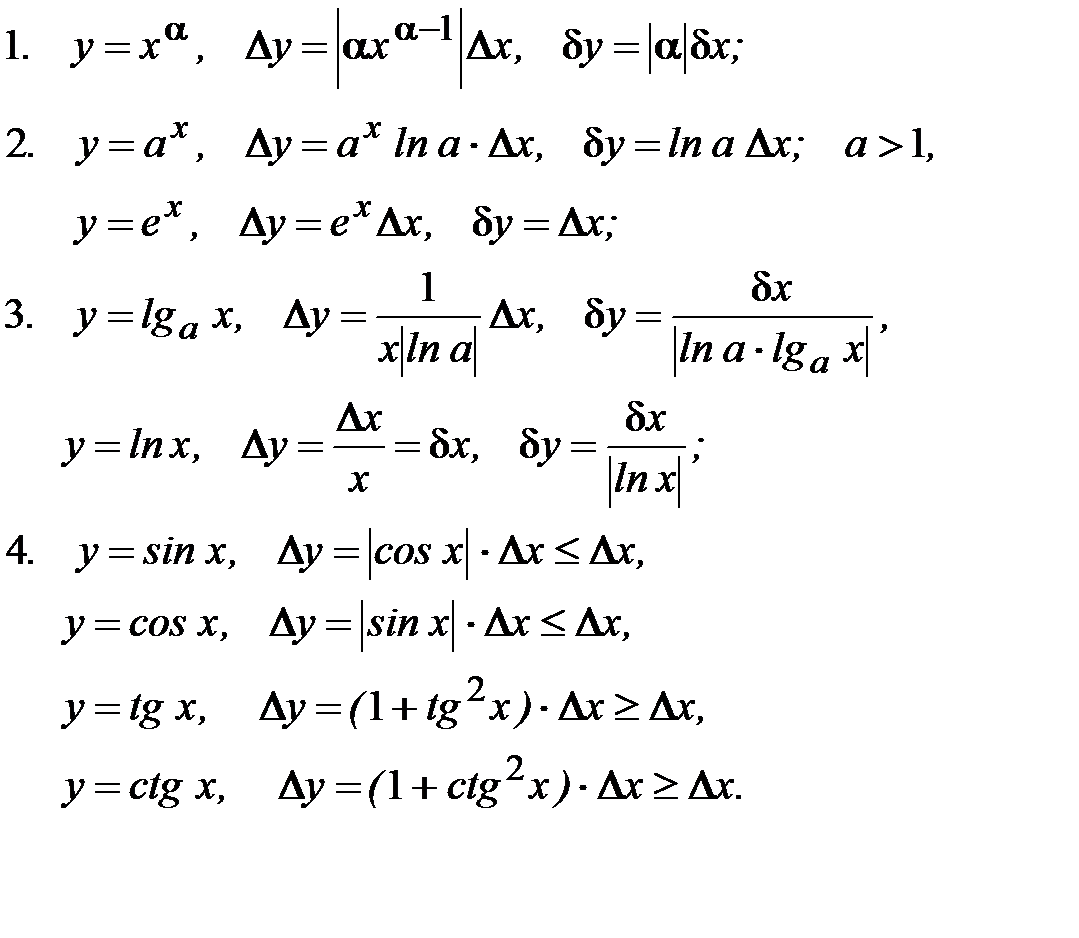
Дата добавления: 2014-12-25