Тест 3. 1. Если при аппроксимации функции f(x) используется способ интерполирования многочленами Pn(x), то какой критерий близости f(x) и Pn(x) при этом

1. Если при аппроксимации функции f(x) используется способ интерполирования многочленами P_n(x), то какой критерий близости f(x) и P_n(x) при этом предполагается?

Варианты ответа:

1) надо, чтобы ׀f(x) - P_n(x)׀ ≤ ε, где ε – требуемая точность аппроксимации

2) надо, чтобы =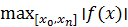

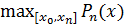
3) совпадение f(x) и P_n(x) в узлах интерполяции

2. В таблице значений функции f(x) имеется 6 значений в соответствующих узлах x_i. Что можно сказать о степени n интерполяционного полинома, проходящего через все эти точки?

Варианты ответа:

1) n = 6

2) n зависит от конкретных значений функции f(x) в узлах x_i

3) n ≤ 5

3. Таблица значений функции f(x) содержит (n+1) точки. Сколько интерполяционных полиномов степени не выше n можно построить по этим точкам?

Варианты ответа:

1) сколько угодно, все зависит от конкретной функции f(x)

2) один единственный

3) n полиномов

4. Интерполяционный полином Лагранжа можно представить в виде:

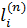L_n(x) = (x) y_i, где (x) =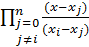

Что можно сказать о величине (x) = z?

Варианты ответа:

1) z зависит от конкретных значений n и x

2) z ≥ 1

3) z = 1

5. Пусть функция f(x) задана таблично с одинаковой абсолютной погрешностью ∆* для всех значений функции. Когда вычислительная погрешность полинома Лагранжа также равна ∆*?

Варианты ответа:

1) всегда

2) когда 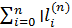(x)׀ = 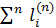(x) = 1

3) никогда, всегда вычислительная погрешность полинома Лагранжа больше ∆*

6. При каком расположении узлов интерполирования x₀, x₁, …, x_n возможно применение интерполяционного полинома Лагранжа?

Варианты ответа:

1) при неравноотстоящих узлах всегда возможно, при равноотстоящих узлах – только для некоторых функций

2) при любом расположении узлов

3) только при неравноотстоящих узлах

7. Для оценки остаточной погрешности интерполяционного полинома используется формула

׀R_n(x*)׀ ≤ ∆₁ = 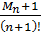׀w(x*)׀

Что представляет собой в этом выражении величина M_n+1?

Варианты ответа:

1)

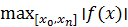
2)

3)

8. Функция f(x) задана таблицей своих значений

Xi	-2	-1
Yi

Какой из указанных полиномов является для нее интерполяционным?

Варианты ответа:

1) P₅(x) = x⁵ – 3x³ +2x² +2

2) P₄(x) = 3x⁴ + 2x² – x + 3

3) P₄(x) = x⁴ – 3x² +2

9. Чему равна разделенная разность f[x₀,x₁,…,x₅] для многочлена
P₅(x) = 3x⁵ – 4x⁴ +2x +1

Варианты ответа:

1) 0

2) 3

3) зависит от конкретных значений

10. Функция f(x) задана таблично. По одним и тем же точкам построены интерполяционный полином Лагранжа и интерполяционный полином Ньютона с разделенными разностями. Что можно сказать об этих полиномах?

Варианты ответа:

1) это два совершенно разных полинома

2) это два разных полинома, но совпадающие в узлах интерполяции

3) это две разные формы одного и того же полинома

Глава 5. ИНТЕРПОЛИРОВАНИЕ С КРАТНЫМИ УЗЛАМИ И СПЛАЙНЫ

Рассмотрим теперь более общую постановку задачи интерполирования полиномами.

В узлах , среди которых нет совпадающих, известны значения функции f(x_i) и ее производных до порядка k_i-1 включительно, . Таким образом, информация о функции f(x) задается следующим образом:

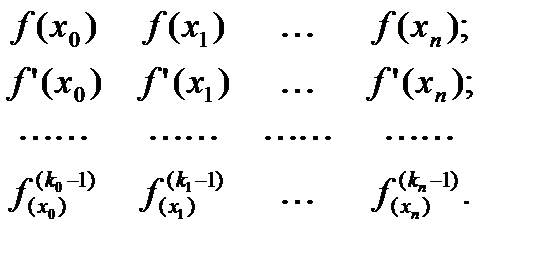(5.1)

Здесь значения для различных i, вообще говоря, различны, но допустим случай, когда . Следовательно, всего задано 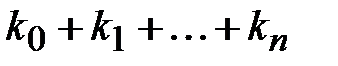величин. Требуется построить алгебраический многочлен 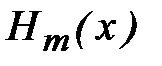степени 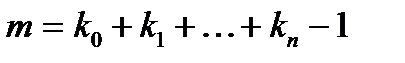, для которого выполняются условия

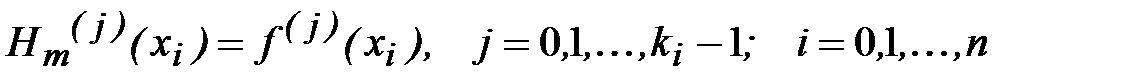. (5.2)

Многочлен 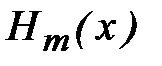, удовлетворяющий условиям (5.2), называется интерполяционным полиномом Эрмита для функции f(x) или интерполяционным полиномом с кратными узлами. Числа называются кратностями узлов 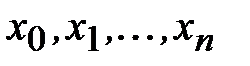соответственно.

Интерполяционный полином 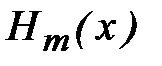определяется единственным образом. В самом деле, предположив противное, будем иметь два полинома степени m, удовлетворяющих условию (5.2). Тогда их разность 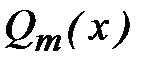удовлетворяет соотношениям

т.е. точки 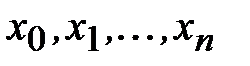являются корнями полинома 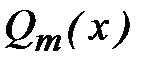кратности соответственно. Мы получили, что многочлен 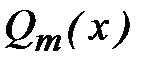степени m имеет m+1 корней. Следовательно, .

Существование интерполяционного полинома Эрмита 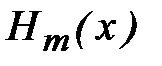докажем, получив для него явное выражение. Далее предположим, что функция f(x) непрерывно дифференцируема (m+1) раз.

§5.1. Разделенные разности с повторяющимися (кратными) узлами

Зададимся последовательностью совокупностей точек

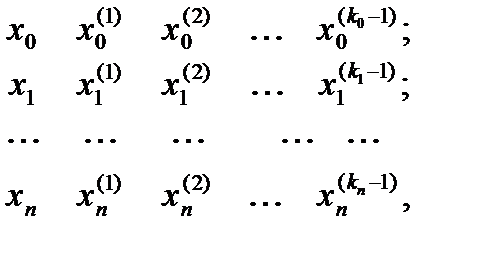
удовлетворяющих условию: все точки – различны. В частности, можно положить

,

где – малая величина. Построим по всем этим точкам разделенную разность порядка 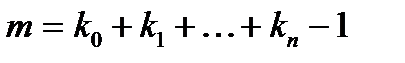. Определим

(5.3)

Рассмотрим сначала случай, когда под знаком разделенной разности левой части (5.3) повторяется только один узел x_i и разделенная разность порядка k_i-1 вычисляется только по этому повторяющемуся узлу. Согласно определению (5.3)

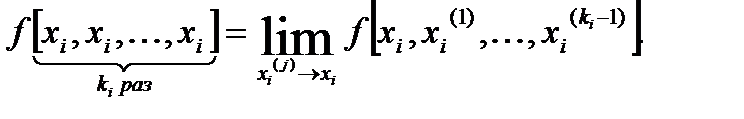
По формуле связи (4.13) между разделенной разностью и производной имеем

(5.4)

где x – точка, принадлежащая наименьшему отрезку, содержащему все точки 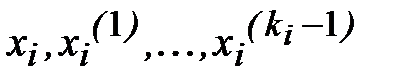. Перейдя в равенстве (5.4) к пределу при 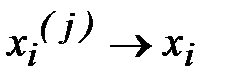, получим

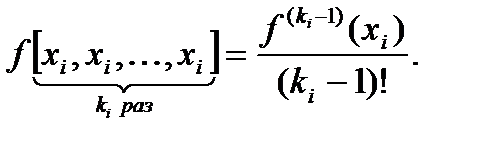(5.5)

Итак, если при производная непрерывна, то существуют разделенные разности

Но это обеспечивает также существование разделенной разности с кратными узлами левой части (5.3), т.к. все остальные разделенные разности, необходимые для ее вычисления, находятся путем последовательного применения рекуррентных формул

и их обобщений. Чтобы не проводить громоздкого вывода для общего случая формулы (5.3), рассмотрим иллюстративную таблицу. Приведенные в этой таблице вычисления переносятся на общий случай без всяких принципиальных затруднений.

Требуется найти 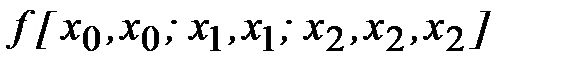, если заданы .

№ строк	xi	f(xi)	f[xi, xj]	Разности II порядка	III пор.	IV пор	V пор	VI пор
	x0	f(x0)
	x0	f(x0)		f[x0; x0, x1]
			f[x0, x1]		f[x0, x0; x1, x1]
	x1	f(x1)		f[x0; x1, x1]		f[x0, x0; x1, x1;x2]
			f’(x1)		f[x0, x1; x1; x2]		f[x0, x0; x1; x1;x2,x2]
	x1	f(x1)		f[x1, x1; x2]		f[x0; x1, x1; x2;x2]		f[x0, x0; x1; x1;x2,x2,x2]
			f[x1, x2]		f[x1, x1; x2, x2]		f[x0; x1, x1; x2,x2,x2]
	x2	f(x2)		f[x1; x2, x2]		f[x1, x1; x2, x2,x2]
			f’(x2)		f[x1; x2; x2, x2]
	x2	f(x2)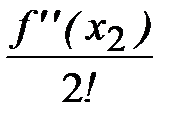
			f’(x2)
	x2	f(x2)

Левый столбец таблицы – для нумерации строк, верхняя строка – для нумерации столбцов. В первом столбце в строках с четным номером приведены аргументы искомой разделенной разности. Во втором столбце в тех строках, что и аргументы, помещены соответствующие значения функции. Третий столбец предназначен для разделенных разностей первого порядка. Они размещаются в строках с нечетными номерами между строк, в которых находятся соответствующие узлы (аргументы) и значения функции. Если узлы повторяются, как это имеет место для строк 1, 5, 9, 11, то сюда помещают значение первой производной. В строках 3, 7 помещены обычные разделенные разности первого порядка. Столбец 4 предназначен для разделенных разностей второго порядка. За исключением последней из них (строка 10), где

,

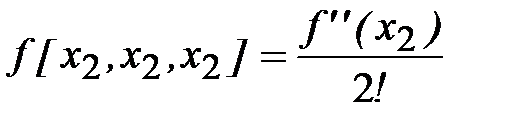они находятся обычным способом по рекуррентной формуле. Так,

.

Аналогично и для остальных разностей. В пятом, шестом, седьмом и восьмом столбцах находятся, соответственно, разделенные разности третьего, четвертого, пятого и шестого порядков. Они вычисляются по обычным рекуррентным формулам. Например,

.

Дата добавления: 2014-12-25