Тест 4

1) Конечная разность связана с соответствующей производной соотношением:

Варианты ответа:

1. ∆^ky_i = k! f^(k)(ξ), ξє [ x_i, x_i+k ];

2. ∆^ky_i = h^k f^(k)(ξ), ξє [ x_i, x_i+k ];

3. ∆^ky_i = kh^k f^(k)(ξ), ξє [ x_i, x_i+1 ].

2) Что можно сказать о величине ∆²у_i для функции у=3х²–2х+5 при шаге h=2. Предполагается, что известны точные значения функции y_i и конечные разности подсчитываются без вычислительной погрешности.

Варианты ответа:

1. ∆²у=0;

2. ∆²у зависит от конкретных значений функции уi и от номера узла;

3. ∆²у = 24.

3) Что такое порядок правильности таблицы конечных разностей?

Варианты ответа:

1. Наивысший порядок конечных разностей, находящихся в таблице;

2. Общее количество конечных разностей в таблице;

3. Порядок последних конечных разностей, которые еще целесообразно использовать в вычислениях.

4) Функция y = sin x, [ 30⁰, 60⁰ ]; h = 5⁰ задана таблицей значений.

Все знаки функции являются верными в узком смысле.

х	у	∆у	∆^2у	∆^3у	∆^4у	∆^5у	∆^6у
30^0	0,5000		– 44	– 5			– 8
35^0	0,5736		– 49	– 5		– 6
40^0	0,6428		– 54	– 3	– 4
45^0	0,7071		– 57	– 7
50^0	0,7660		– 64
55^0	0,8192
60^0	0,8660

Примечание: Все конечные разности приведены в единицах последнего разряда значений функции. Какую степень n интерполяционного полинома разумно выбрать в данных условиях?

Варианты ответа:

1. n = 6;

2. n = 3;

3. n = 4.

5) Функция y = lg x задана таблично:

х	2,0	2,1	2,2	2,3	2,4	2,5
у	0,30103	0,32222	0,34242	0,36173	0,38021	0,39794

Надо найти значение функции в точке х* = 2,48. Какой интерполяционной формулой целесообразно воспользоваться?

Варианты ответа:

1. Формулой Бесселя;

2. Первой формулой Ньютона;

3. Второй формулой Ньютона.

6) Функция у = е^х задана таблично:

х	3,50	3,55	3,60	3,65	3,70	3,75
у	33,115	34,813	36,598	38,475	40,447	42,521

Надо найти значение функции в точке х* = 3,61. Какой интерполяционной формулой целесообразно воспользоваться?

Варианты ответа:

1. Первой формулой Ньютона;

2. Формулой Бесселя;

3. Формулой Стирлинга.

7) Функция у = sin xзадана таблично:

х	1^0	2^0	3^0	4^0	5^0	6^0
у	0,0174	0,0349	0,0523	0,0697	0,0871	0,1045

Надо найти значение функции в точке х* = 1,4⁰. Какой интерполяционной формулой целесообразно воспользоваться?

Варианты ответа:

1. Второй формулой Ньютона;

2. Формулой Стирлинга;

3. Первой формулой Ньютона.

8) Функция у = задана таблично:

х	2,70	2,72	2,74	2,76	2,78	2,80
у	0,3704	0,3676	0,3650	0,3623	0,3597	0,3571

Надо найти значение функции в точке х* = 2,75. Какой интерполяционной формулой целесообразно воспользоваться?

Варианты ответа:

1. Формулой Стирлинга;

2. Формулой Бесселя;

3. Первой формулой Ньютона.

9) Что можно сказать о степени интерполяционных полиномов Стирлинга и Бесселя?

Варианты ответа:

1. Полином Бесселя является полином четвертой степени, а полином Стирлинга – четвертой;

2. Полином Бесселя является полиномом нечетной степени, а полином Стирлинга – четной;

3. Оба полинома могут иметь любые степени, все зависит от конкретной функции.

10) В какой интерполяционный полином входят величины

у₀, 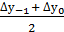, ∆²у_–1, , ∆⁴у_–2 и т. д.

Варианты ответов:

1. Полином Бесселя;

2. Полином Стирлинга;

3. Как в полином Бесселя, так и в полином Стирлинга.

Глава 6. Численное дифференцирование

К численному дифференцированию приходится прибегать в том случае, когда функция f(x), для которой нужно найти производную, задана таблично или же имеет сложное аналитическое выражение. В первом случае методы дифференциального исчисления просто неприменимы, а во втором случае их использование вызывает значительные трудности.

Одним из способов построения формул численного дифференцирования является дифференцирование интерполяционных полиномов. Пусть известны значения функции f(x) в точках 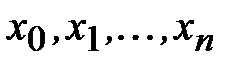. Требуется вычислить . Построим интерполяционный полином L_n(x) и положим

. (6.1)

Точно так же мы можем заменять значения производных функций значениями производных других интерполяционных полиномов: Стирлинга, Бесселя и т.д. Можно показать [3], что остаточный член формул численного дифференцирования (6.1) имеет следующий вид:

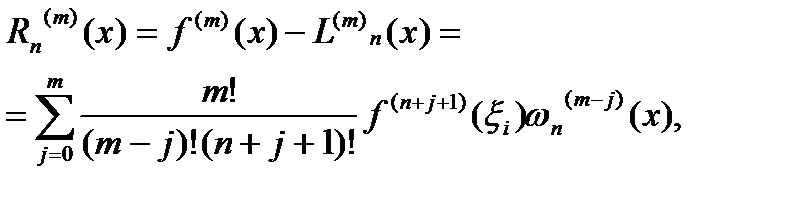(6.2)

где ,

а 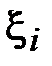– некоторые точки из интервала между наименьшим и наибольшим из чисел x, .

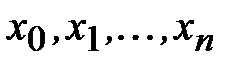Пусть функция задана на равномерной сетке узлов с шагом h. Взяв интерполяционный полином Стирлинга, построенный по точкам 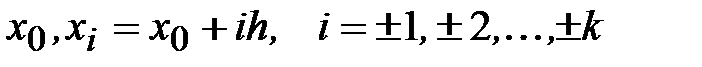, продифференцируем его один раз. Получим следующую формулу для первой производной:

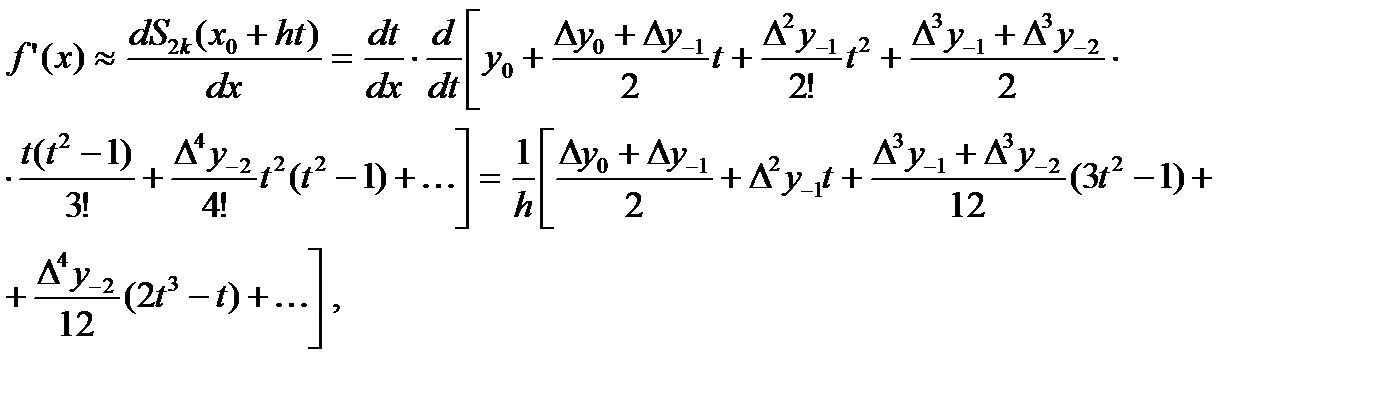(6.3)

где .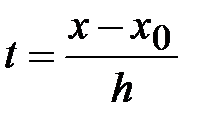

Для второй производной, дифференцируя по х (6.3), получим

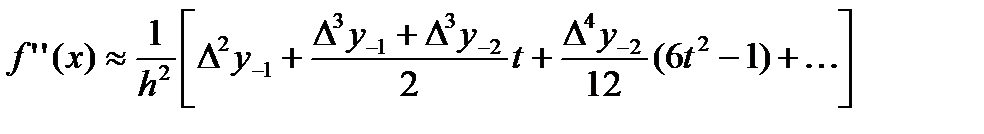(6.4)

В частности, при x=x₀ (t=0) будем иметь

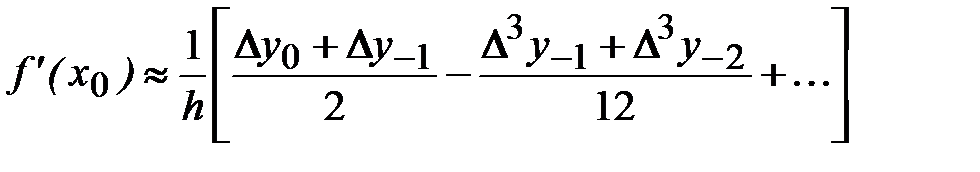(6.5)

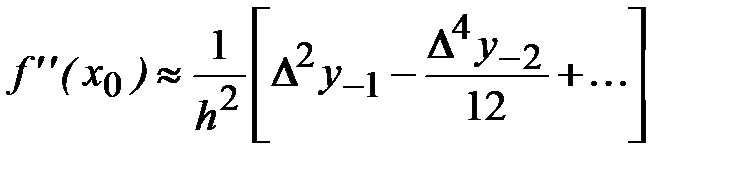(6.6)

В некоторых случаях выгоднее выражать производные в узловых точках не через конечные разности, а непосредственно через значения функции. Преобразуем к такому виду формулы (6.5) и (6.6).

Если в формулах (6.5) и (6.6) ограничиться одним слагаемым, что соответствует полиному Стирлинга второй степени, то получим соответственно

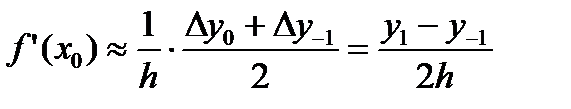; (6.7)

. (6.8)

Взяв в формулах (6.5) и (6.6) по два слагаемых (полином Стирлинга четвертой степени), будем соответственно иметь

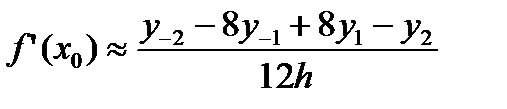; (6.9)

. (6.10)

Получим остаточный член формулы численного дифференцирования (6.5). Для этого продифференцируем по х остаточный член полинома Стирлинга степени 2k и подставим x=x₀ :

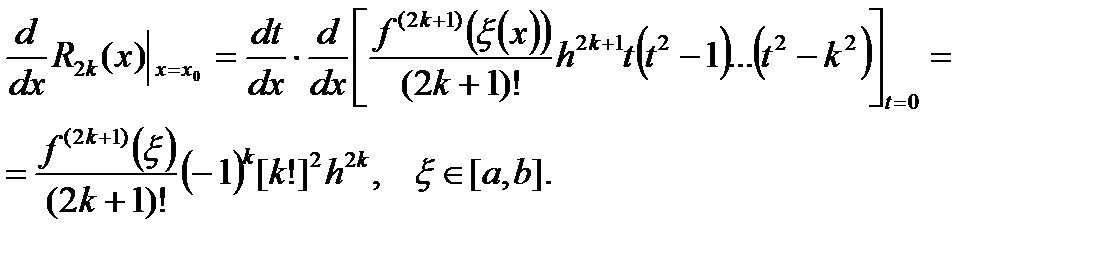(6.11)

Для формул (6.7) и (6.9) остаточный член (6.11) будет соответственно иметь вид

.

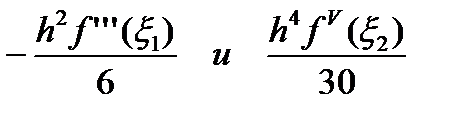Исследуем полную погрешность формул численного дифференцирования, например, для формулы (6.7)

, (6.12)

где ,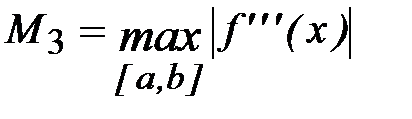

– абсолютная погрешность каждого из чисел y_i.

В (6.12) первое слагаемое (остаточная погрешность) убывает с уменьшением h, а второе (вычислительная погрешность) возрастает с уменьшением h. Возникает вопрос о подборе для данной формулы численного дифференцирования оптимального шага h^*, для которого полная погрешность имела бы минимальное значение. Найдем такой шаг

,

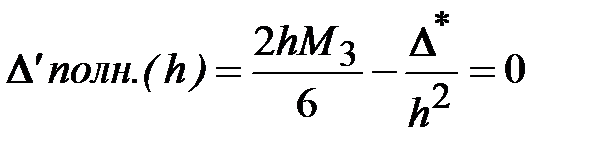откуда

.

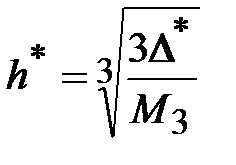В точке h = h^* функция 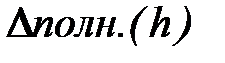имеет действительно минимальное значение, поскольку

.

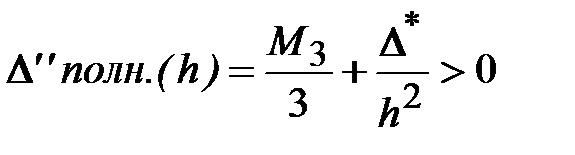При вычислении второй производной или производных более высокого порядка, когда в знаменатель соответствующей формулы численного дифференцирования входит h² или h^k и k>2, вопрос о выборе оптимального шага является еще более актуальным.

Тренировочные задания.

Задание I.

Функция f(x) задана таблицей своих значений, верных в написанных знаках. Найти первую производную этой функции в точках x₁^*=0,7 и x₂^*=1,0. Оценить погрешности результатов. Найти оптимальный шаг h^* для каждой из формул численного дифференцирования.

Xi	0,5	0,6	0,7	0,8	0,9	1,0
yi	0,4794	0,5646	0,6442	0,7174	0,7833	0,8415

Дата добавления: 2014-12-25