Тест 5

1. На основании какого интерполяционного многочлена получена формула численного дифференцирования

y₀′ = f′(x₀) ≈ (∆y₀ - ∆²y₀ + ∆³y₀ - … + (-1)^n-1 ∆ⁿy₀)

Варианты ответа:

1) на основании второго интерполяционного многочлена Ньютона

2) на основании первого интерполяционного многочлена Ньютона

3) на основании интерполяционного многочлена Стирлинга

2. На основании какого интерполяционного многочлена получена формула численного дифференцирования

y₀′ = f′(x₀) ≈ (∆y_-1 + ∆²y_-2 + ∆³y_-3 + … + ∆ⁿy_-n)

Варианты ответа:

1) на основании первого интерполяционного полинома Ньютона

2) на основании второго интерполяционного полинома Ньютона

3) на основании интерполяционного полинома Стирлинга

3. С помощью какого интерполяционного многочлена получена формула численного дифференцирования

y₀′′ = f′′(x₀) ≈ 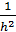(∆²y_-1 - ∆⁴y_-2 + ∆⁶y_-4 + …)

Варианты ответа:

1) с помощью второго интерполяционного многочлена Ньютона

2) с помощью интерполяционного многочлена Стирлинга

3) с помощью первого интерполяционного многочлена Ньютона

4. С помощью какого интерполяционного многочлена получена формула численного дифференцирования

y₀′′ = f′′(x₀) ≈ 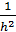(∆²y_-2 + ∆³y_-3 + 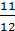∆⁴y_-4 + ∆⁵y_-5 +…)

Варианты ответа:

1) с помощью интерполяционного многочлена Стирлинга

2) с помощью второго интерполяционного многочлена Ньютона

3) с помощью первого интерполяционного многочлена Ньютона

5. Почему на практике редко применяют формулы численного дифференцирования для производных выше второго порядка?

Варианты ответа:

1) расчетные формулы получаются слишком громоздкими

2) с ростом порядка производных обычно резко падает точность численного дифференцирования

3) численные оценки производных выше второго порядка обычно мало интересны

6. Что происходит с остаточной погрешностью численного дифференцирования при увеличении шага h таблицы значений функции?

Варианты ответа:

1) погрешность почти не меняется

2) уменьшается

3) увеличивается

7. Что происходит с вычислительной погрешностью численного дифференцирования при увеличении шага h таблицы значений функции?

Варианты ответа:

1) увеличивается

2) почти не меняется

3) уменьшается

8. Что такое оптимальный шаг численного дифференцирования?

Варианты ответа:

1) шаг, при котором конечные разности находятся в определенных пределах

2) шаг, при котором сумма остаточной и вычислительной погрешности данной формулы численного дифференцирования достигает минимального значения

3) шаг, при котором для данной формулы численного дифференцирования минимальна остаточная погрешность

9. Чему равна вычислительная погрешность формулы численного дифференцирования

y₀′′ ≈ =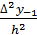

если h = 0,01, а ∆^*y = 0,0005

Варианты ответа:

1) 0,05

2) 0,1

3) 0,2

10. Шаг таблицы значений функции увеличился в 4 раза. Что можно сказать о конечных разностях третьего порядка?

Варианты ответа:

1) они практически не изменились

2) увеличились в 4 раза

3) увеличились в 4³ = 64 раза

Глава 7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Пусть требуется вычислить интеграл

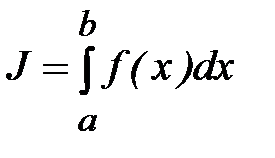. (7.1)

Если функция f(x) является непрерывной на отрезке [a, b], то интеграл (6.1) существует и может быть вычислен по формуле Ньютона-Лейбница

. (7.2)

Однако для большинства функций f(x) первообразную F(x) не удается выразить через элементарные функции. Кроме того, функция f(x) часто задается в виде таблицы ее значений для определенных значений аргумента. Все это порождает потребность в построении формул численного интегрирования или квадратурных формул.

Приближенное равенство

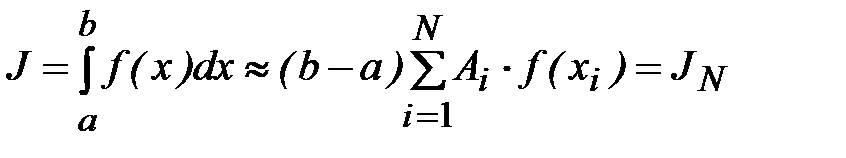(7.3)

называется квадратурной формулой, определяемой узлами и коэффициентами A_i.

Величина

(7.4)

называется остаточным членом квадратурной формулы.

В зависимости от способа задания подынтегральной функции f(x) будем рассматривать два различных в смысле реализации случая численного интегрирования.

Задача 1. На отрезке [a, b] в узлах x_i заданы значения f_i некоторой функции f, принадлежащей определенному классу F. Требуется приближенно вычислить интеграл (7.1) и оценить погрешность полученного значения.

Так обычно ставится задача численного интегрирования в том случае, когда подынтегральная функция задана в виде таблицы.

Задача 2. На отрезке [a, b] функция f(x) задана в виде аналитического выражения. Требуется вычислить интеграл (7.1) с заданной предельно допустимой погрешностью e.

Рассмотрим алгоритм решения задач 1 и 2.

Алгоритм решения задачи 1.

1. Выбирают конкретную квадратурную формулу (7.3) и вычисляют J_N. Если значения функции f(x) заданы приближенно, то фактически вычисляют лишь приближенное значение для точного J_N.

2. Приближенно принимают, что .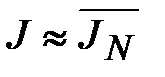

3. Пользуясь конкретным выражением для остаточного члена 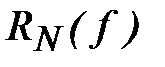или оценкой его для выбранной квадратурной формулы, вычисляют погрешность метода

.

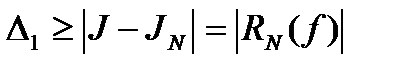4. Определяют погрешность вычисления

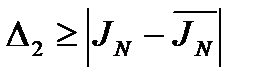
по погрешностям приближенных значений f(x_i).

5. Находят полную абсолютную погрешность приближенного значения :

.

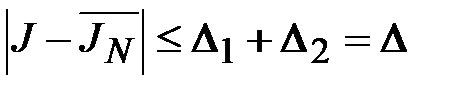6. Получают решение задачи в виде

.

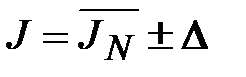Алгоритм решения задачи 2.

1. Представляют e в виде суммы трех неотрицательных слагаемых:

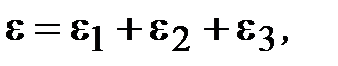
где e₁ – предельно допустимая погрешность метода: e₂ – предельно допустимая погрешность вычисления ; e₃ – предельно допустимая погрешность округления результата.

2. Выбирают N в квадратурной формуле так, чтобы выполнялось неравенство

.

3. Вычисляют f(x_i) с такой точностью, чтобы при подсчете по формуле (6.3) обеспечить выполнение неравенства

.

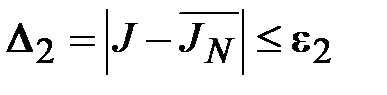Для этого, очевидно, достаточно вычислить все f(x_i) с абсолютной погрешностью

.

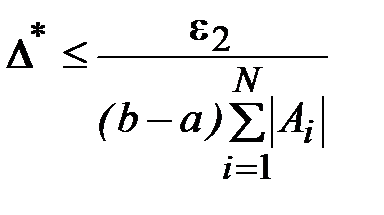4. Найденную в п.3. величину округляют (если ) с предельно допустимой погрешностью 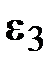до величины .

5. Получают решение задачи в виде

.

Дата добавления: 2014-12-25