Правило Рунге практической оценки погрешности квадратурных формул. Уточнение приближенного значения интеграла по Ричардсону

Пусть функция и интеграл (7.1) вычисляется по формуле прямоугольников. Получим следующее соотношение:

, (7.30)

где с – постоянная, не зависящая от h.

Введем вспомогательную функцию

.

Очевидно, что

(7.31)

Разложим функцию F(x) в ряд Тейлора в окрестности точки .

(7.32)

С помощью (7.31) и (7.32) имеем

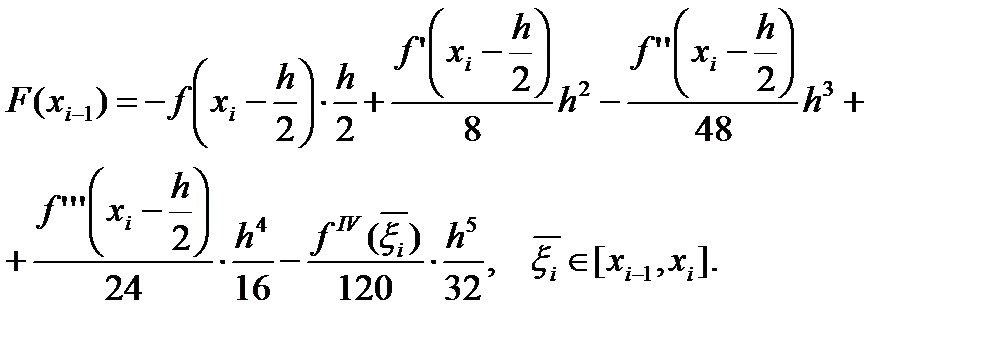
Вычитая из верхнего равенства нижнее, получим

(7.33)

откуда

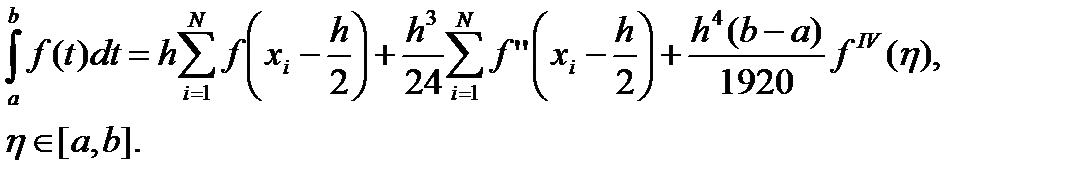(7.34)

На основании (7.11)

,

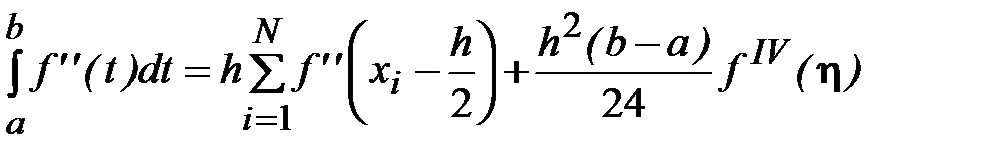откуда

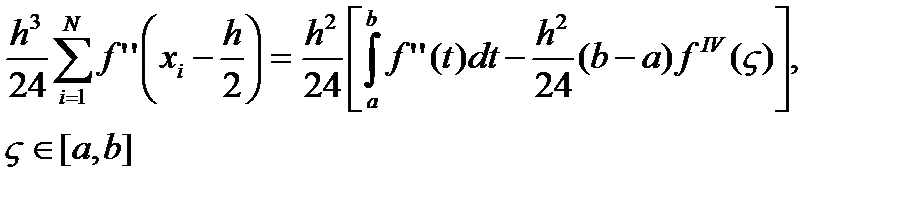(7.35)

Подставим (7.35) в (7.34):

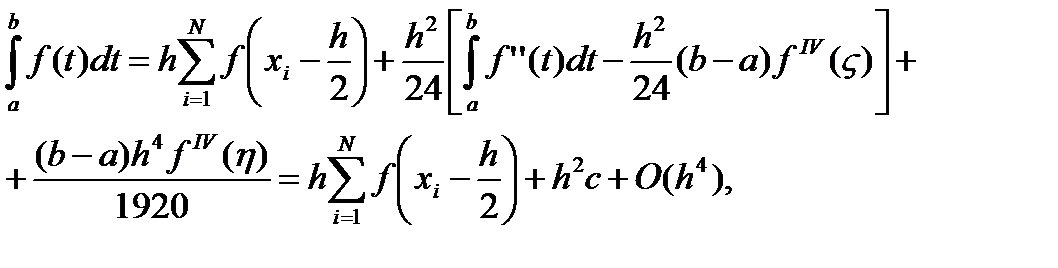
где не зависит от h. Соотношение (7.30) получено. Величина ch² называется главной частью погрешности формулы прямоугольников.

Если , то справедливо аналогичное соотношение и для формулы трапеций

, (7.36)

где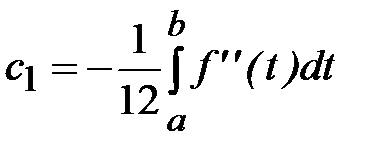

не зависит от h.

При условии можно получить аналогичное соотношение для формулы Симпсона

, (7.37)

где – не зависящая от h постоянная.

Обозначим через J_h приближенное значение интеграла (7.1), найденное по одной из трех формул: прямоугольников, трапеций, Симпсона, и объединим соотношения (7.30), (7.36), (7.37) в одно

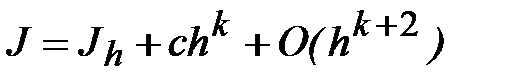, (7.38)

где с не зависит от h, k = 2 для формул прямоугольников и трапеций, k = 4 для формулы Симпсона. Предполагается, что . Запишем соотношение (7.38) для h₁ = 2h:

, (7.39)

вычтем из (6.39) (6.38) и получим

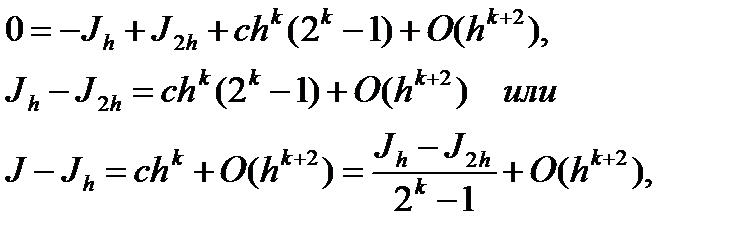
следовательно, с точностью до имеем

. (7.40)

Вычисление приближенной оценки погрешности квадратурной формулы по формуле (7.40) называется правилом Рунге.

Вычитая из умноженного на 2^k равенства (7.38) равенство (7.39), получим

, (7.41)

откуда

. (7.42)

Число называется уточненным по Ричардсону приближенным значением интеграла J.

Согласно (6.42)

.

Таким образом, с помощью приближенных значений интегралов J_h, J_2h, найденных по соответствующим квадратурным формулам с шагом h и 2h, можно, во-первых, оценить погрешность более точного значения интеграла J_h по правилу Рунге и, во-вторых, вычислить уточненное по Ричардсону приближенное значение интеграла , имеющее погрешность более высокого порядка относительно h, чем J_h.

Тренировочные задания.

Задание I.

Вычислить с помощью формулы прямоугольников

с точностью 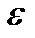= 10^-2.

Задание II.

Вычислить 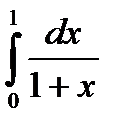по формуле трапеций, полагая N=4; оценить полную погрешность результата.

Задание III.

Вычислить 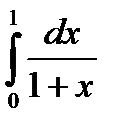по формуле Симпсона с точностью .

Дата добавления: 2014-12-25