Метод Эйлера. Метод решения дифференциального уравнения разложением в ряд Тейлора может быть использован как численный метод решения

Методы Рунге-Кутта.

Метод решения дифференциального уравнения разложением в ряд Тейлора может быть использован как численный метод решения. Пусть требуется найти решение уравнения (1) с начальным условием (2) на отрезке .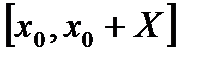

Разобьем отрезок 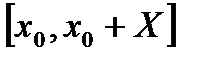на N частей точками

(10)

Решение в точке находим по формулам (8), (9). Затем, принимая найденное решение за начальное приближенное, находим решение в точке 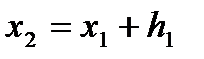и т.д. Если решение в точке 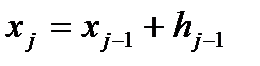уже найдено, т.е. 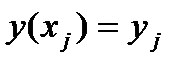, то вычисляем значение производных, входящих в разложение (8), в точке 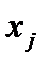по формулам (9); а затем по формуле (8) находим

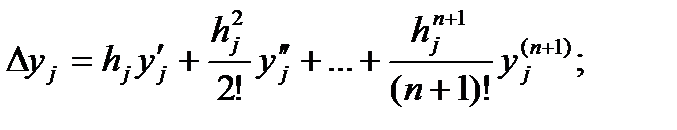(11)

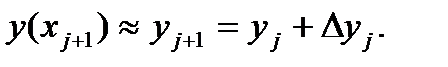
В частном случае при использовании в формуле (11) одного члена получим:

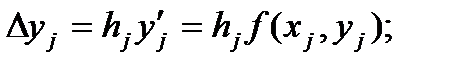(12)

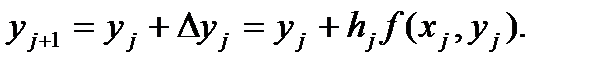
Метод решения дифференциальных уравнений, основанный на формуле (12), называется методом Эйлера. Метод Эйлера является частным, простейшим случаем методов типа Рунге-Кутта, к построению которых мы и переходим в дальнейшем. Метод Эйлера, как и некоторые другие методы, основывается на следующем. Пусть известно значение решения дифференциального уравнения (1) в точке и требуется вычислить значение Заменим дифференциальное уравнение (1) с начальным условием 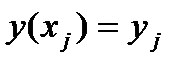равносильным ему интегральным уравнением:

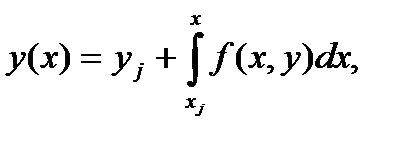(13)

откуда

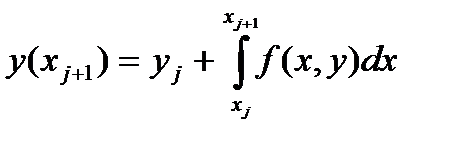(14)

Заменим интеграл в правой части (14) по формуле прямоугольников, т.е.

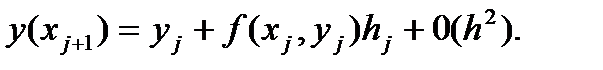(15)

Отбрасывая член 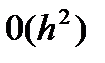, получаем расчетную формулу метода Эйлера (12). Геометрический смысл метода Эйлера ясен из рис.1. На каждом отрезке 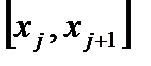приращение функции 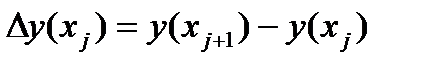заменяется приращением ординаты касательной к графику 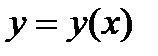заменяется ломаной линией; каждое звено этой ломаной 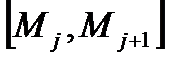, называемой ломаной Эйлера, имеет направление, совпадающее с направлением касательной к графику интегральной кривой, проходящей через точку . Первое звено касается истинной интегральной кривой в точке .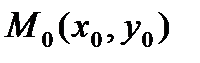

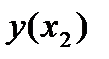
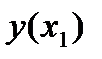
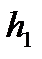
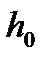
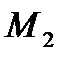
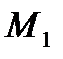
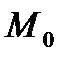
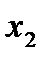
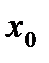
x

y

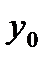
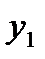
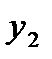
Пример 3. Методом Эйлера построить таблицу решений уравнения с начальным условием y(0) =1на отрезке 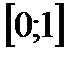с шагом h =0,1.

Решение. На основании формулы (12) имеем

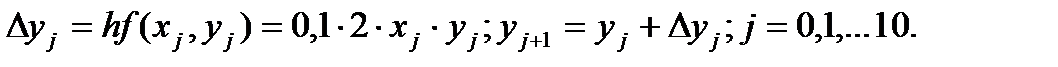(16)

Результаты вычислений приведены в таблице 1.

Таблица 1.

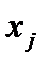
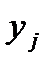
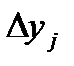
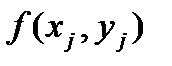
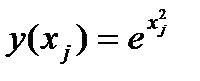
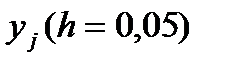
0.0   0.1   0.2   0.3   0.4   0.5   0.6   0.7   0.8   0.9   1.0	1.000   1.000   1.020   1.061   1.125   1.215   1.337   1.497   1.707   1.980   2.336	0.000   0.020   0.041   0.064   0.090   0.122   0.160   0.210   0.273   0.356	0.000   0.200   0.408   0.637   0.900   1.215   1.604   2.096   2.731   3.564	1.000   1.010   1.041   1.094   1.173   1.284   1.433   1.632   1.896   2.248   2.718	1.00   1.01   1.04   1.09   1.16   1.26   1.39   1.57   1.80   2.12   2.53

Таблица заполняется следующим образом. В первой строке записываются начальные значения 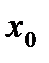=0; 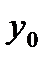=1.000 и по ним вычисляется 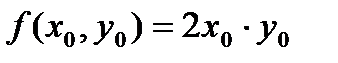=0, а затем получаем 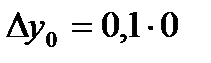=0. Тогда по формуле (16) при j =0 получаем

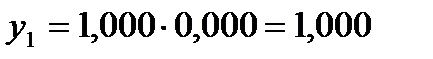
Значения 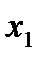=0,1 и 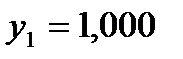записываются во второй строке таблицы и т.д. В пятом столбце таблицы для сравнения приведены значения точного решения 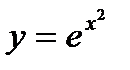. Сравнение результатов показывает, что абсолютная погрешность при X=0,5 равна

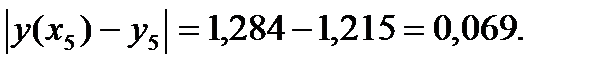
при X=1 - 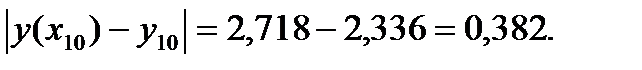Погрешность, как мы видим, увеличивается к концу отрезка /накапливается/. Для того чтобы уменьшить погрешность, необходимо уменьшить шаг h. В шестом столбце таблицы приведены результаты вычислений по методу Эйлера с h =0,05 (значения функций в точках 0,05 0,15 и т.д. в таблице 1 не указаны). Здесь абсолютная погрешность при X=0,5, равна ≈0,02: при X=1 ≈0,2. Как будет показано ниже, погрешность метода Эйлера можно оценивать методом двойного просчета: сначала вычисляют значение 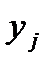с шагом h, а затем с шагом 2h и погрешность более точного значения (при шаге h) оценивают приближенно величиной

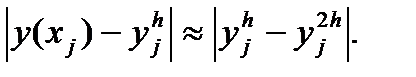(17)

Так в нашем примере погрешность 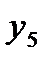, найденного с шагом h =0,05, равна

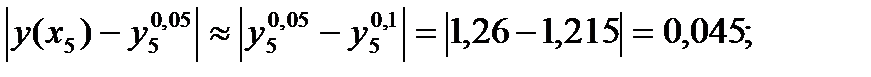
погрешность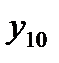

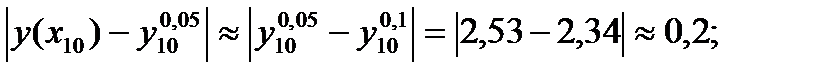
Достоинством метода Эйлера является его простота, недостатком – большая погрешность и систематическое накопление погрешности.

Дата добавления: 2014-12-25