Метод Рунге-Кутта решения систем дифференциальных уравнений первого порядка

Рунге.

Оценка погрешности формул Рунге-Кутта по правилу

При применении любой формулы Рунге-Кутта погрешность на одном шаге оценивается величиной 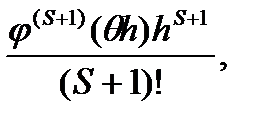где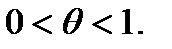

Главный член погрешности на одном шаге есть

(77)

Точка находится близко от точки 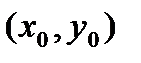(h-мало), поэтому погрешность на следующем шаге будет иметь такой же главный член.

В результате двух шагов будет найдено приближение к значению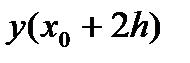

такое, что 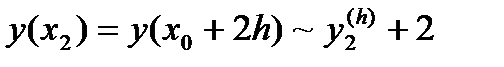(78)

Если, исходя из точки 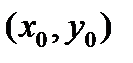, применить формулу Рунге-Кутта с шагом 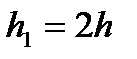, то получим приближение 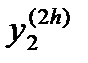к значению 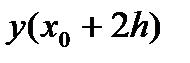, для которого

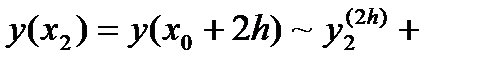
(79)

Из этих соотношений вытекает представление главного члена погрешности на шаге

(80)

В результате проведённого рассуждения мы имеем возможность через каждые два шага, получая приближенное значение , иметь также выражение главного члена его погрешности.

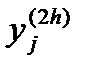Указанный приём оценки погрешности на шаге называется приёмом(методом) Рунге. При реализации метода Рунге-Кутта на ЭВМ с автоматическим выбором шага h в каждой второй точке делают двойной просчёт: сначала находят решение с шагом h, затем с шагом 2h.

Если величина 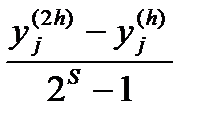не превышает заданной погрешности 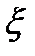, то продолжают вычисления с тем же шагом h, в противном случае берут шаг

Очевидно, что в рассматриваемых ранее частных случаях выражение главного члена погрешности будет иметь вид:

1. Для метода Эйлера (S=1, S+1=2)

(81)

2. Для метода Эйлера-Коши уточнённого метода Эйлера(S=2)

(82)

3. Для формулы Рунге-Кутта при r = 4, S = 4

(83)

Пример 6. Методом Рунге-Кутта (69)-(71) построить таблицу решений задачи Коши

(84)

на отрезке с точностью

Решение. Поскольку формула Рунге-Кутта (69)-(71) имеет на одном шаге погрешность 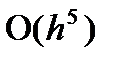, то погрешность на всём отрезке будет порядка Поэтому выбирая шаг из соотношения т.е.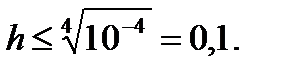

Все вычисления будем вести с одним запасным знаком. В процессе решения задачи через каждые два шага будем контролировать пригодность выбранного шага методом двойного просчёта по формуле (83). Результаты вычислений, проводимых по формулам 85, 86. удобно располагать по схеме, приведённой в таблице 4.

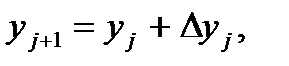(85)

(86)

Таблица 4.

J	x	y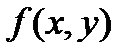
J

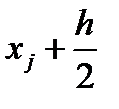
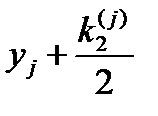
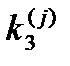
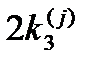
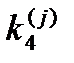
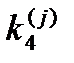
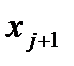
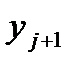
Результаты решения задачи Коши (84) представлены в таблице 4, которая заполняется

следующим образом. В столбец (I) заносим номер итерации (j=0), в столбец (2) и (3) первой строки записываем значения , (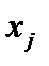

Вычисляем = = 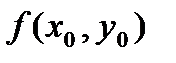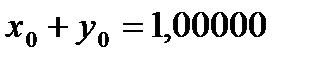и записываем в столбец (4) первой строки.

Затем находим умножая соответствующее значение на 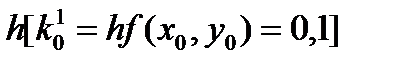. Так как в выражение для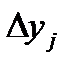 входит с коэффициентом I, то записываем значение в (6)-й столбец первой строки. Во (2)-м и (3)-м столбцах второй строки записываем аргументы для в (4)-й столбец записываем значение значение функции от сформированных аргументов . Затем умножая на h, вычисляем 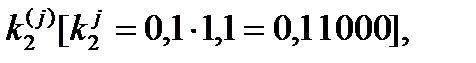В (6)-й столбец заносим удвоенное значение Третья и четвертая строки заполняются аналогично, согласно таблице 4.

После заполнения 4-й строки находится сумма чисел в (6)-м столбце и умножается на 1/6, т.е. определяется . Значение добавляется к и записывается в первую строку следующей итералии.

Таблица 5.

I	x	y
	0.0 0.05 0.05 0.1	1.00000 1.05000 1.05500 1.11050	1.00000 1.10000 1.10500 1.21050	0.10000 0.11000 0.11050 0.12105	0.10000 0.22000 0.22100 0.12105
	0.1 0.15 0.15 0.2	1.11034 1.17086 1.17638 1.24298	1.21034 1.32086 1.32638 1.44298	0.12103 0.13209 0.13264 0.14430	0.12103 0.26417 0.26528 0.14430
	0.2	1.24280

В результате двух шагов полученно значение Для определения погрешности на шаге вычислим значение с шагом . Результаты вычислений помещены в таблице 6.

Таблица 6.

X	y
0.0 0.1 0.1 0.2	1.00000 1.10000 1.12000 1.24400	1.00000 1.20000 1.22000 1.44400	0.20000 0.24000 0.24400 0.28880	0.20000 0.48000 0.48800 0.28880
0.2	1.24280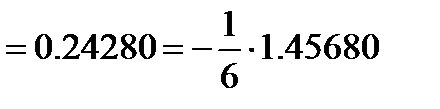

На основании (83) погрешность более точного значения не превосходит , т.к.

.

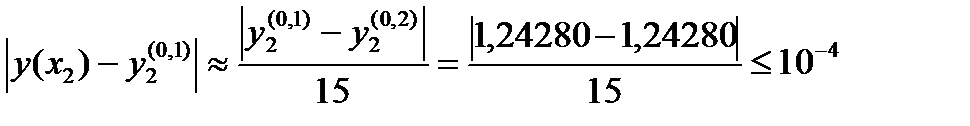Таким образом, выбранный шаг 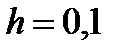обеспечивает нужную точность вычислений. Поэтому переходим к вычислению с тем же шагом. Результаты вычислений с и с приведены в таблице 7.

Таблица 7.

I	x	y
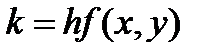
	0.20 0.25 0.25 0.30	1.24280 1.31494 1.32104 1.39990	1.44280 1.56494 1.57104 1.69990	0.14428 0.15649 0.15710 0.16999	0.14428 0.31299 0.31421 0.16999
	0.30 0.35 0.35 0.4	1.39971 1.48470 1.49144 1.58385	1.69971 1.83470 1.84144 1.98385	0.16997 0.18347 0.18414 0.19838	0.16997 0.36694 0.36829 0.19838
	0.4
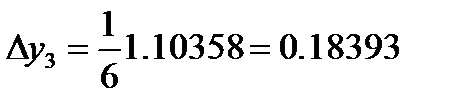
	0.2 0.3 0.3 0.4		1.44280 1.68708 1.71151 1.98510	0.28856 0.33742 0.34230 0.39705	0.28856 0.67484 0.68460 0.39702
	0.4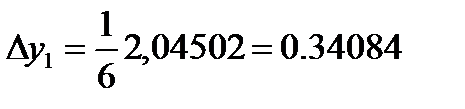

На основании оценки (83) вновь убеждаемся в пригодности выбранного шага. Продолжая вычисления аналогичным образом, найдем значения искомого решения на всем отрезке .

; ; ; ; ; .

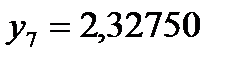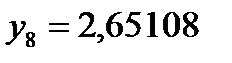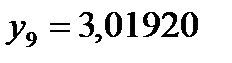Вычислив значения 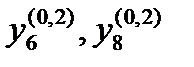и с двойным шагом, убедимся, что полученные значения с шагом 0,1 имеют погрешность, не превышающую .

Метод Рунге легко переносится на системы обыкновенных уравнений. Для сокращения записи ограничимся системой двух уравнений первого порядка.

z’=g(x,y,z) (87)

С начальными условиями:

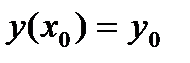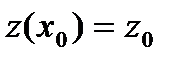, (88)

Как и в случае одного уравнения будем вычислять

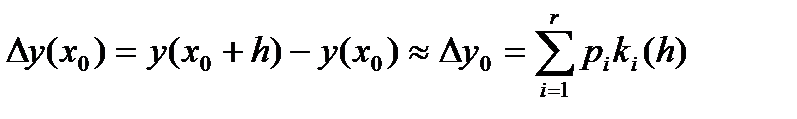(89)

(90)

Где

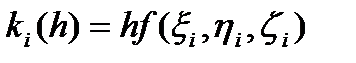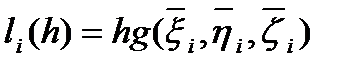, (91)

, , , ;

,

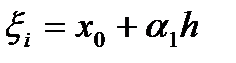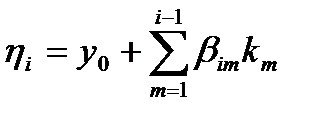(92)

Выбор постоянных величин производится так, чтобы разложения функции и по степеням hначинались с возможно более высоких степеней h, где

(93)

(94)

Формулы (89)-(92) для различных r,будут иметь различный вид и разную погрешность на одном шаге.

Получим формулу Рунге-Кутта (89)-(92)для r=4, которые на одном шагеиметь погрешность порядка 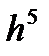. Для этого необходимо иметь погрешность порядка. Для этого необходимо, чтобы функции и обладали свойством:

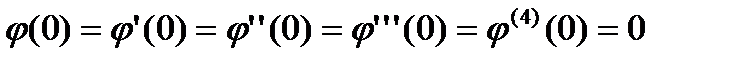(95)

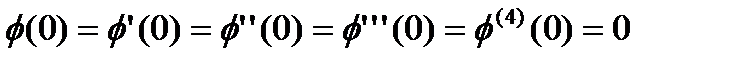(96)

Приравнивание нулю произвольных функций и 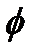дает, как и в случае одного уравнения, систему уравнений относительно постоянных величин , которая имеет бесчисленное множество решений. Выбирая любые решенияэтой системы, получим различные формулы Рунге-Кутта, имеющие порядок погрешности на одном шаге .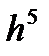

Наиболее употребительными из формул Рунге-Кутта с погрешностьюна на шаге порядка 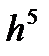с погрешностью на шаге порядка 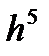являются формулы:

,

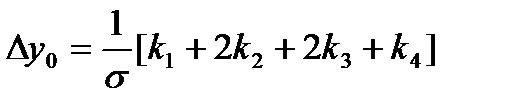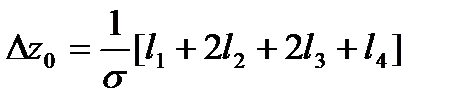, (97)

, ,

,

,

,

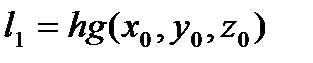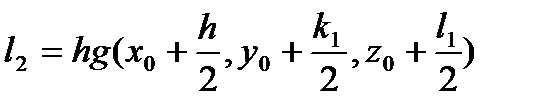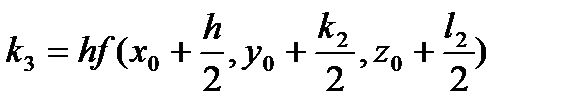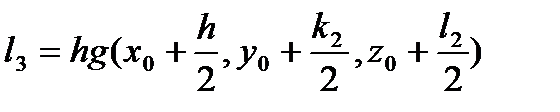, (98)

,

.

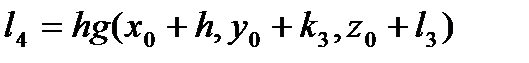Практически погрешность можго оценивать методом двойного просчета.

Пример7. Методом Рунге-Кутта (97)-(98) найти решение системы диффиринциальных уравнений

y’=z+1, z’=y-x (99)

с начальным условием y(0)=I; z(0)=I на отрезке [0,0; 0,4] взяв шаг h=0,2. Оценить погрешность полученного решения методом двойного просчета.

Решение. Так как погрешность расчетных формул (97)-(98) на одном шаге имеет порядок h⁵ = (0,2)⁵ =0,00032, то вычисления необходимо вести по крайней мере с четырьмя верными знаками после запятой. Результаты вычислений по формулам (97)-(98) с шагом h=0,2 помещены в таблице 8. Вычисления с удвоенным шагом h=0,4 – двойной просчет – помещены в таблице 9. На основании приближенной оценки погрешности (83) получаем:

Таблица 8

x	Y	z	f	G	k	l	Δy	Δz
0,0	1,0000	1,0000	2,0000	1,0000	0,4000	0,2000	0,4000	0,2000
0,1	1,2000	1,1000	2,1000	1,1000	0,4200	0,2200	0,8400	0,4400
0,1	1,2100	1,1100	2,1100	1,1100	0,4220	0,2220	0,8440	0,4440
0,2	1,4220	1,2220	2,2220	1,2220	0,4444	0,2444	0,4444	0,2440
							0,4214	0,2214
0,2	1,4214	1,2214	2,2214	1,2214	0,4443	0,2443	0,4443	0,2443
0,3	1,6435	1,3435	2,3435	1,3435	0,4687	0,2687	0,9374	0,5374
0,3	1,6558	1,3558	2,3558	1,3558	0,4712	0,2712	0,9424	0,5424
0,4	1,8926	1,4926	2,4926	1,4926	0,4985	0,2985	0,4985	0,2985
0,4	1,8919	1,4919					0,4705	0,2705

Таблица 9

x	Y	z	f	G	k	l	Δy	Δz
0,0	1,0000	1,0000	2,0000	1,0000	0,8000	0,4000	0,8000	0,4000
0,2	1,4000	1,2000	2,2000	1,2000	0,8800	0,4800	1,7600	0,9000
0,2	1,4400	1,2400	2,2400	1,2400	0,8960	0,4960	1,7920	0,9920
0,4	1,8960	1,4960	2,4960	1,4960	0,9984	0,5984	0,9984	0,5984
0,4	1,8912	1,4912					0,8912	0,4912

Дата добавления: 2014-12-25