Оценка остаточного члена кстраполяционной формулы Адамса

Оценим остаточный член экстраполяционной формулы Адамса.

Например, формула Адамса (122) получена при замене функции , входящей в правую часть выражения (112), второй интерполяционной формулой Ньютона третьего порядка.

(124)

Где 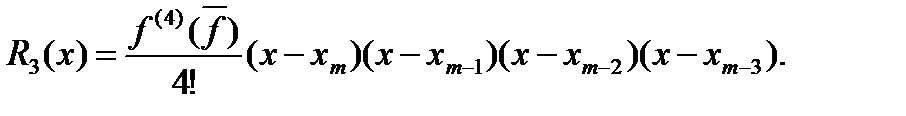(125)

Подставляя (124) в (112), получим

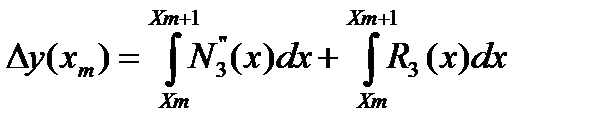(126)

После интегрирования первый член правой части (126) дает формулу Адамса (122), второй член – величину остаточного члена этой формулы

(127)

Сделав в (127) замену переменной

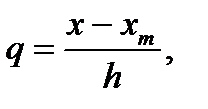(128)

Получаем

(129)

Произведение 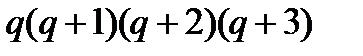не меняем знака на отрезке [0,I], поэтому на основании теоремы о среднем можно написать:

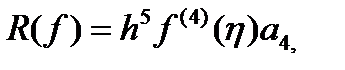или (130)

Где

Из выражения (130) следует, что экстраполяционная формула Адамса (122) имеет на одном шаге погрешность порядка .

Очевидно, что в общем случае при использованиии экстраполяционной формулы Адамса до разностей включительно погрешность на одном шаге будет иметь порядок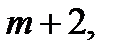

Т.е. (131)

Пример 9. Используя условия примера 6, вычислитьзначение решения дифференциального уравнения в точках 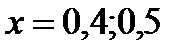по экстраполяционной формуле Адамса.

Решение. В примере 6 с помощью метода Рунге-Кутта были вычислены значения искомой ф-ции при Используя эти значения (), продолжим вычисления по формуле (123). Результаты вычислений приведены в таблице 11.

Таблица 11.

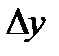
			F (x, y)	G=hf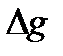
0,0	1,00000		1,00000	0,15555
0,1	1,11034		1,21034	0,121034	21034
0,2	1,24280		1,44280	0,144280	23246	2212
0,3	1,39971		1,69971	0,169971	25691	2445	233
		0,183922			28392	2701	256
0,4	1,58363		1,98063	0,198363
		0,213781
0,5	1,79741

Порядок заолнения таблицы 11:

1)Запсывая знасения 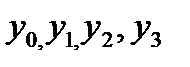, полученные в примере 6 в таблицу 11, находтсоответствующие значения 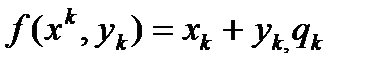и состовляем таблицу разностей.

2)по формуле (123) вычисляем

3) Вычисляем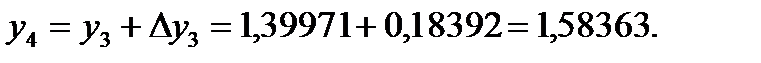

4) Записываем значение в таблицу, и аналогичным образом вычисяляес

Отсюда

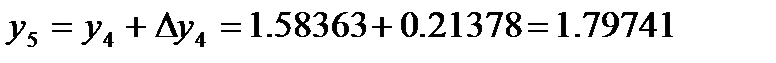
Дата добавления: 2014-12-25