Метод Милна решения дифференциальных уравнений

Методом Адамса.

Решение систем дифференциальных уравнений

Метод Адамса легко распространяется на системы

(155)

При начальных условиях 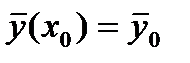, где - вектор функции

(156)

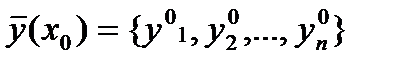
Зная векторный начальный отрезок 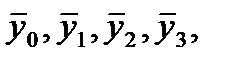последующие значения координат искомой вектор функции определяем, используя экстраполяционную формулу Адамса.

. (157)

Для контроля вычислений используем интерполяционную формулу Адамса

. (158)

Погрешность полученного решения оценивается так же как и в случае одного уравнения.

Одним из наиболее простых и практических удобных численных методов решения дифференциальных уравнений является метод Милна.

Пусть дано дифференциальное уроавнение

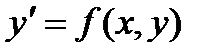(159)

С начальным условием

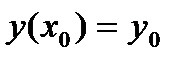(160)

Требуется найти решение этого уравнения на отрезке

Выбрав шаг 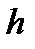, положим

. (161)

Предположим, что нам известны первые четыре значения искомого уравнения - «Начальный участок», которые могут быть найдены одним из методов, описанных выше, например, методом Рунге-Кутта. Следовательно, известны значения функции

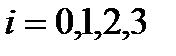(162)

Значение искомого решения в точке определяем, интегрируя уравнение (159) в пределах от до . Учитывая условие (160), получим

(163)

Используя значение функции 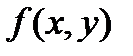в точках и первую интерполяционную формулу Ньютона, запишем:

, (164)

Где - (165)

- остаточный член Т интерполяционной формулы Ньютона.

Подставляя (164) в (163) почленно интегрируя, получим

(166)

Или

,

Или

(167)

Где

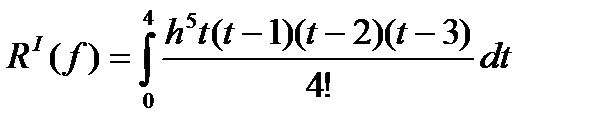(168)

Отбрасывая в (167) остаточный член 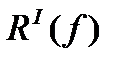, получаем приближенную формулу:

(169)

Так как

,

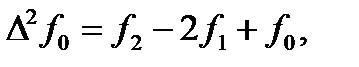(170)

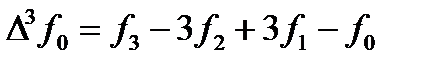
То, подставляя значения разностей в формулу (169), получим первую формулу Милна

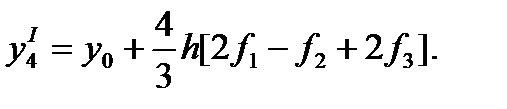(171)

В общем случае, предполагая известными значения искомого решения в точках 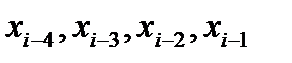т.е. значения 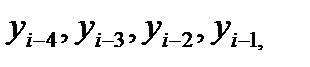вычисляем значение в точке 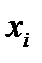по первой формуле Милна

(172)

Как и в случае расчетных формул Адамса можно получить вторую контрольную формулу Милна. Для ее вывода проинтегрируем уравнение (159) в пределах от 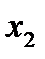до и запишем первую интерполяционную формулу Ньютона для функции 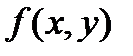, взяв за начальную точку не 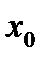, а . Тогда получим:

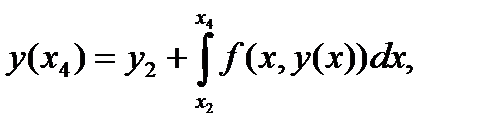(173)

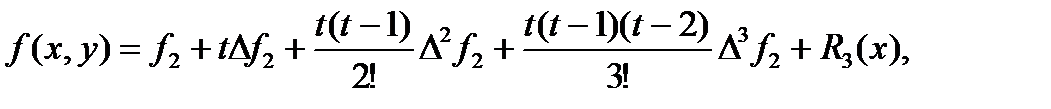(174)

Где

(175)

Подставляя (174) в (173) и почленно интегрируя, получим:

(176)

Где

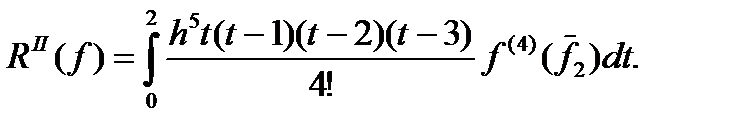(177)

Отбрасывая в выражении (176) остаточный член и используя представления разностей через значения функций получим вторую формулу Милна

(178)

В общем случае при определении значения искомого решения в точке вторая формула Милна будет иметь вид

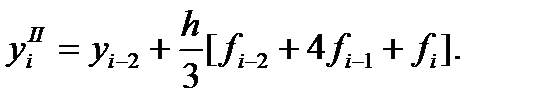(179)

Вторая формула Милна как и Интерполяционная Адамса не может быть использована для вычисления значения , так как входит в обе части равенства (179) но она может быть использована для контроля вычислений, производимых по первой формуле Милна.

Погрешность I и II формул Милна на одном шаге определяется выражениями (168) и (177) соответственно. Как и в случая экстраполяционной и интерполяционной формулы Адамса, погрешность значения , полученного по II формуле, определяется выражением

(180)

Замечание из выражений для остаточного члена I и II формул Милна очевидно, что погрешность обеих формул на одном шаге имеет порядок 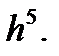Погрешность приближенного решения, получаемого по формулам Милна на всем отрезке , есть величина порядка , поэтому первоначальный шаг обычно выбирается из условия , где 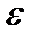- заданная допустимая погрешность. В процессе вычисления пригодность выбранного шага проверяется на основании выражения (180).

Пример 13. Используя I и II формулы Милна найти в условиях примера в решение при 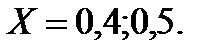Оценить погрешность.

Решение. В качестве начального отрезка используем значения решения в точка 0,0; 0,1; 0,2; 0,3, найденных методом Рунге-Кутта.

Запишем значения 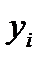и функции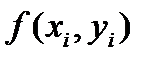 в таблицу 13.

Вычислим по I формуле Милна (171) .

Записываем полученное значение в ьаблицу 13 в первую из строк, соответствующую формулу i=4.

Таблица 13.

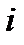
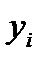
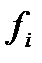
	0,1	1,00000	1,00000
	0,1	1,11034	1,21034
	0,2	1,24280	1,44280
	0,3	1,39972	1,69972
	0,4	1,58364	1,98364
0,4	1,58364	1,98364
	0,5	1,79743	2,29743
0,5	1,79744	2,29744

Затем вычисляем .

Далее, применяя II формулу Милна (178), вычисляем 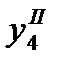еще раз

.

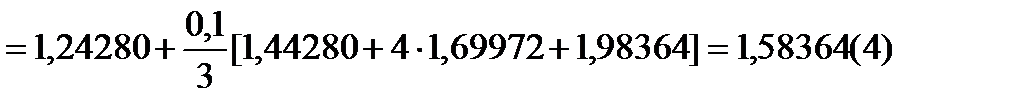Записываем найденное значение 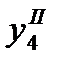и соответствующие значение во вторую строку при i=4.

Оцениваем погрешность значениея , полученного по второй формуле Милна на основании выражения (180)

.

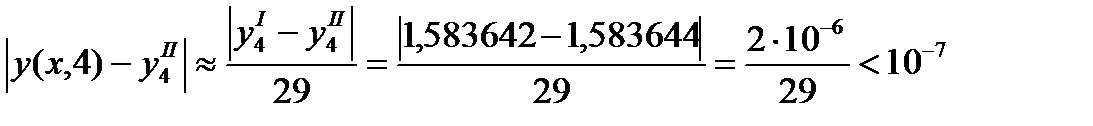Таким образом, имеет все написанные знаки верными в узком смысле слова.

Далее аналогичным образом вычисляем 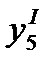и , и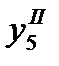спользуя значения и , найденные по второй контрольной формуле Милна.

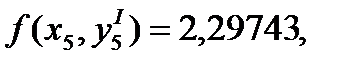
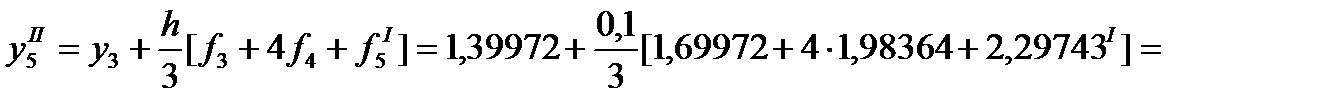
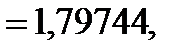
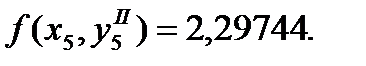
Погрешность 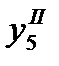определяется вличиной

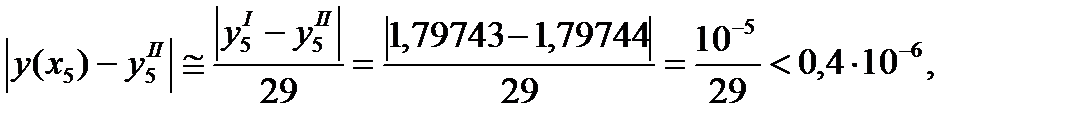то есть 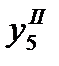имеет все написанные знаки верными в узком смысле слова.

Тренировочные задание.

Задание I.	Решить дифференциальное уравнение с начальным условием y(1)=2,70 на интервале [1; 1,5] методом Эйлера, принимая h=0,125. Все вычисления вести с тремя верными в узком смысле знаками.
Задание II.	Решить методом Эйлера-Коши уравнение 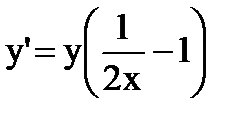с начальным условием y(1)=2,70 на интервале [1; 2], принимая h=0,25. Все вычисления вести с тремя верными в узком смысле знаками.
Задание III.		Решить методом Рунге-Кутта уравнение 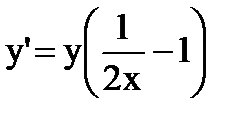с начальным условием y(1)=2,70 на интервале [1; 2], принимая h = 0,5. Все вычисления вести с тремя верными в узком смысле знаками.

Решение тренировочного задания.

Задание I.

По исходным начальным данным x0=1 и y0=2,70 вычисляем 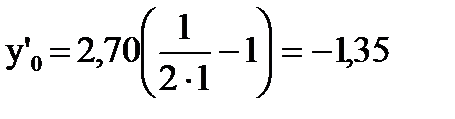. Далее, следуя формуле (4), имеем Dy0=-0,169. Таким образом, по формуле (5) получаем y1=2,70–0,169=2,53.

Дальнейшие вычисления выполняем аналогично, принимая за исходные значения x1,y1; x2,y2 и так далее. Результаты вычислений представлены в следующей таблице.

i	xi	yi	y'i = f(xi,yi)	Dyi = hf(xi,yi)
	1,000	2,70	–1,35	–0,169
	1,125	2,53	–1,41	–0,176
	1,250	2,35	–1,41	–0,176
	1,375	2,17	–1,38	–0,172
	1,500	2,00

Задание II.

По исходным начальным данным x0 = 1 и y0 = 2,70 вычисляется y'0=–1,35. Затем вычисляются вспомогательные величины и 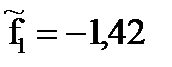. Наконец, по формуле (7) вычисляется y1=2,70–0,35=2,35.

Принимая теперь за исходные данные x1=1,25 и y1=2,35, дальнейшие вычисления выполняем аналогично вышеприведенным, а их результаты представим в виде следующей таблицы:

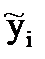
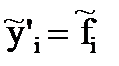
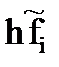
i	xi	yi	y'i=fi	hfi				Dyi-1
	1,00	2,70	–1,35	–0,338
	1,25	2,35	–1,41	–0,352	2,36	–1,42	–0,355	–0,346
	1,50	2,01	–1,34	–0,355	2,00	–1,33	–0,332	–0,342
	1,75	1,69	–1,21	–0,302	1,68	–1,20	–0,300	–0,318
	2,00	1,41			1,39	–1,04	–0,260	–0,281

Задание III.

;

;

;

.

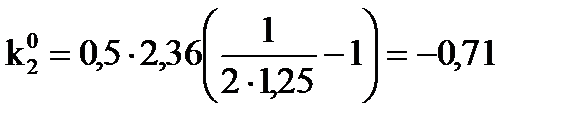По формуле (8) имеем:

.

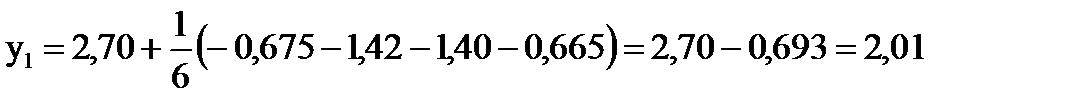Вычисление y2 = y(2,0) аналогично вычислению y1, а результат его представлен в следующей таблице:

i	x	Y	f(x,y)	k1,2k2,2k3,k4	Dy
	1,00 1,25 1,25 1,50	2,70 2,36 2,34 2,00	–1,35 –1,42 –1,40 –1,33	–0,675 –1,42 –1,40 –0,665	–0,693
	1,50 1,75 1,75 2,00	2,01 1,68 1,71 1,40	–1,34 –1,20 –1,22 –1,05	–0,670 –1,20 –1,22 –0,525	–0,602
	2,00	1,41

Глава 9. Практикум.

Задача А.

Задача 1.

Дано приближенное число 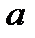= 88,325 и известно, что у этого числа три верных значащих цифры в широком(узком) смысле. Оценить абсолютную и относительную погрешность в обоих случаях.

Дата добавления: 2014-12-25