Стирлинга, Бесселя

Б1. Интерполирование с помощью полинома Лагранжа

Со сколькими верными знаками необходимо взять значение указанной функции в точках x_i, чтобы вычислить значение функции в точке x^* с минимальной погрешностью. Вычислить результат.

y=cos x; y=ln x;

1. x_i=20^o, 22^o, 25^o, 26^o; x^*=23^o. 21. x_i=2; 2,5; 3; 4; x^*= e.

2. x_i=27^o, 28^o, 30^o, 32^o; x^*=29^o. 22. x_i=10, 13, 14, 16; x^*=11.

3. x_i=30^o, 31^o, 33^o, 35^o; x^*=32^o. 23. x_i=11, 13, 16, 18; x^*=12.

4. x_i=35^o, 38^o, 40^o, 43^o; x^*=37^o. 24. x_i=1, 2, 4, 5; x^*= e.

5. x_i=40^o, 45^o, 48^o, 51^o; x^*=43^o. 25. x_i=5, 6, 8, 9; x^*=7.

y=sin x; y=lg x;

5. x_i=7^o, 9^o, 14^o, 17^o; x^*=12^o. 11. x_i=6, 8, 11, 12; x^*=10.

6. x_i=15^o, 18^o, 21^o, 23^o; x^*=20^o. 12. x_i=9, 12, 15, 19; x^*=10.

7. x_i=17^o, 22^o, 25^o, 30^o; x^*=28^o. 13. x_i=98, 102, 107, 112; x^*=100.

8. x_i=25^o, 29^o, 34^o, 37^o; x^*=30^o. 14. x_i=110, 115, 119, 121; x^*=113.

9. x_i=40^o, 45^o, 51^o, 55^o; x^*=50^o. 15. x_i=115, 119, 124, 128; x^*=120.

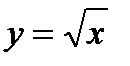
16. x_i=14, 16, 19, 21; x^*=17.

17. x_i=15, 18, 21, 23; x^*=20.

18. x_i=12, 14, 17, 19; x^*=16.

19. x_i=20, 22, 26, 29; x^*=25.

20. x_i=8, 10, 11, 13; x^*=9.

Задача Б2. Интерполирование с помощью формул Ньютона,

Используя таблицу значений функции (все приведенные знаки верны в узком смысле):

а) составить таблицу конечных разностей;

б) вычислить значения функции для указанных значений аргументов и оценить погрешность результатов.

xi	yi		1. x1^*=1,18; x2^*=1,38;
1,1	0,89121		x3^*=1,25; x4^*=2,16.
1,2	0,93204		2. x1^*=1,12; x2^*=1,46;
1,3	0,96356		x3^*=1,55; x4^*=2,18.
1,4	0,98545		3. x1^*=1,16; x2^*=1,57;
1,5	0,99750		x3^*=1,65; x4^*=2,17.
1,6	0,99957		4. x1^*=1,15; x2^*=1,75;
1,7	0,99166		x3^*=1,88; x4^*=2,14.
1,8	0,97385		5. x1^*=1,17; x2^*=1,66;
1,9	0,94630		x3^*=1,95; x4^*=2,15.
2,0	0,90930
2,1	0,86321
2,2	0,80850

xi	yi		6. x1^*=0,504; x2^*=0,524;
0,50	1,6487		x3^*=0,535; x4^*=0,604.
0,51	1,6653		7. x1^*=0,503; x2^*=0,533;
0,52	1,6820		x3^*=0,545; x4^*=0,603.
0,53	1,6989		8. x1^*=0,502; x2^*=0,542;
0,54	1,7160		x3^*=0,555; x4^*=0,602.
0,55	1,7333		9. x1^*=0,506; x2^*=0,556;
0,56	1,7507		x3^*=0,565; x4^*=0,606.
0,57	1,7683		10. x1^*=0,508; x2^*=0,568;
0,58	1,7860		x3^*=0,575; x4^*=0,608.
0,59	1,8040
0,60	1,8221
0,61	1,8404

xi	yi		11. x1^*=1013; x2^*=1043;
	3,00432		x3^*=1065; x4^*=1113.
	3,00860		12. x1^*=1012; x2^*=1032;
	3,01284		x3^*=1055; x4^*=1112.
	3,01703		13. x1^*=1014; x2^*=1054;
	3,02119		x3^*=1075; x4^*=1114;
	3,02531		14. x1^*=1016; x2^*=1066;
	3,02938		x3^*=1085; x4^*=1116.
	3,03342		15. x1^*=1018; x2^*=1078;
	3,03743		x3^*=1095; x4^*=1118.
	3,04139
	3,04532
	3,04922

xi	yi		16. x1^*=2,706; x2^*=2,756;
2,70	0,3704		x3^*=2,77; x4^*=2,906.
2,72	0,3676		17. x1^*=2,708; x2^*=2,768;
2,74	0,3650		x3^*=2,87; x4^*=2,908.
2,76	0,3623		18. x1^*=2,709; x2^*=2,769;
2,78	0,3597		x3^*=2,81; x4^*=2,909.
2,80	0,3571		19. x1^*=2,712; x2^*=2,772;
2,82	0,3546		x3^*=2,85; x4^*=2,912.
2,84	0,3521		20. x1^*=2,715; x2^*=2,835;
2,86	0,3497		x3^*=2,89; x4^*=2,915.
2,88	0,3472
2,90	0,3448
2,92	0,3425

xi	yi		21. x1^*=0,63; x2^*=0,88;
0,6	1,8221		x3^*=1,05; x4^*=1,63.
0,7	2,0138		22. x1^*=0,68; x2^*=0,93;
0,8	2,2255		x3^*=1,25; x4^*=1,68.
0,9	2,4596		23. x1^*=0,64; x2^*=1,07;
1,0	2,7183		x3^*=1,45; x4^*=1,64.
1,1	3,0042		24. x1^*=0,67; x2^*=1,22;
1,2	3,3201		x3^*=1,15; x4^*=1,67.
1,3	3,6693		25. x1^*=0,66; x2^*=1,34;
1,4	4,0552		x3^*=0,95; x4^*=1,66.
1,5	4,4817
1,6	4,9530
1,7	5,4739

Задача В.

При численном решении многих практических задач часто возникает необходимость получить значения производных различных порядков функции y=f(x), заданной в виде таблицы или в виде сложного аналитического выражения, непосредственное дифференцирование которого затруднено. В таких случаях используются приближенные методы дифференцирования.

Рассматривается следующая задача:

На сетке 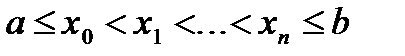в узлах x_i заданы значения y_i=f(x_i) функции f(x), непрерывно дифференцируемой n+1+m раз. Требуется вычислить производную и оценить погрешность.

Один из возможных путей решения этой задачи заключается в применении теории интерполирования. Построим для функции f(x) по узлам x_i, i=0,1,...,n интерполяционный полином P_n(x) с остаточным членом R_n(x) так, что

. (1)

Продифференцируем правую и левую части соотношения (1) по x m раз и положим x=x^*

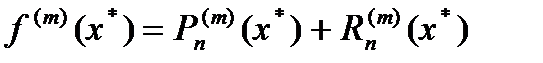. (2)

Производная от многочлена P_n^(m)(x) применяется для приближенного представления искомой производной f^(m)(x):

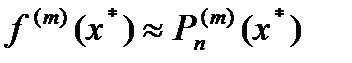. (3)

Вычисление высших производных может быть сведено к последовательному вычислению низших, поэтому мы остановимся более подробно на получении расчетных формул для 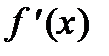. Приближенные формулы для вычисления производных в начале и в конце таблицы получаются путем дифференцирования интерполяционных многочленов Ньютона, а для вычисления производных в середине таблицы - путем дифференцирования интерполяционных многочленов Стирлинга и Бесселя.

Например, если выбрать узлы x₀,x₁,x₂,x₃,x₄ и воспользоваться первым интерполяционным многочленом Ньютона, то мы получим формулу численного дифференцирования вида

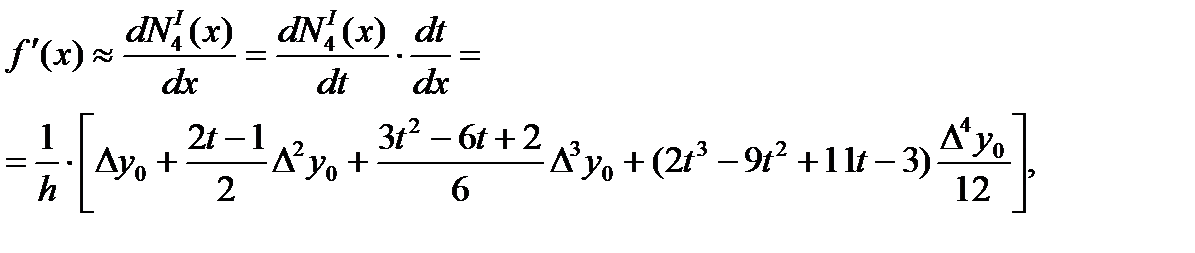(4)

где .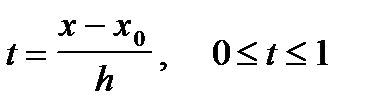

На практике часто выгоднее выражать значения производных не через конечные разности, а непосредственно через значения функции в узлах. Для получения таких безразностных формул удобно воспользоваться многочленом Лагранжа с равномерным расположением узлов (x_i-x_i-1=h, i=1,2,...,n).

Запишем многочлен Лагранжа второй степени (три узла интерполирования).

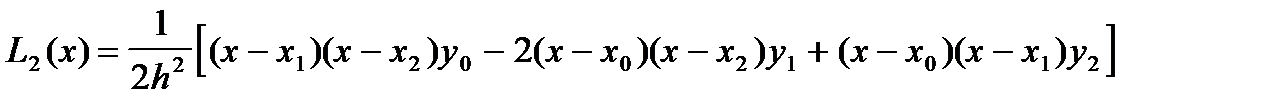(5)

Тогда

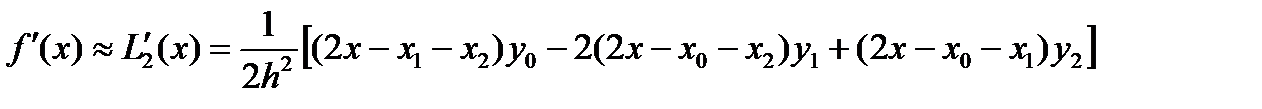(6)

В основном формулы численного дифференцирования применяют для вычисления производных в узлах x_i. Подставим в равенство (6) последовательно значения x=x₀;x₁;x₂. Получим:

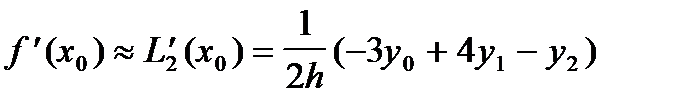;	(7)
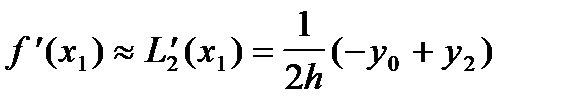;	(8)
.	(9)

Остаточные члены формул численного дифференцирования (7) - (9) получим дифференцированием остаточного члена

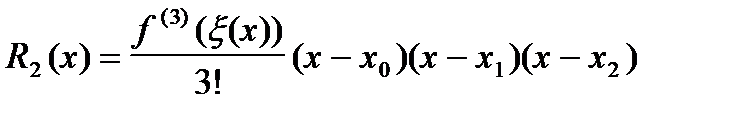
многочлена Лагранжа (5) и последовательной подстановкой в выражение для 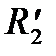значений x=x₀;x₁;x₂.

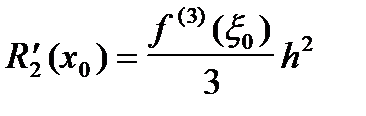;	(10)
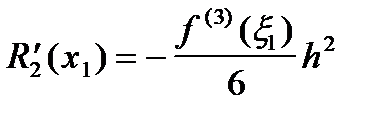;	(11)
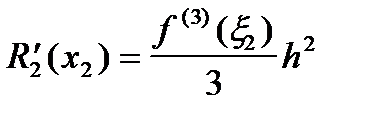.	(12)

Записывая интерполяционный многочлен Лагранжа третьей степени (четыре узла) и его остаточный член, получим следующие формулы для производных в узлах:

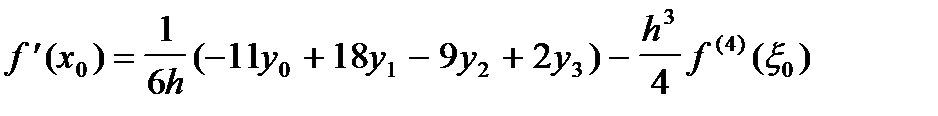;	(13)
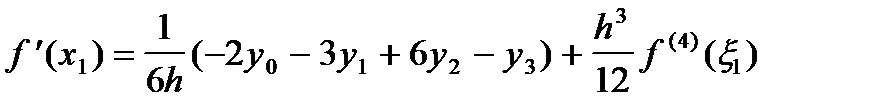;	(14)
;	(15)

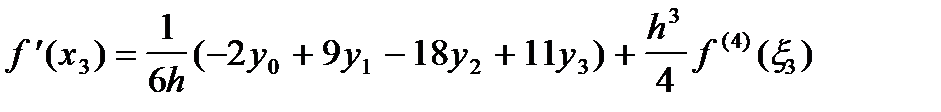. (16)

В случае многочлена четвертой степени (пять узлов) получим:

;	(17)
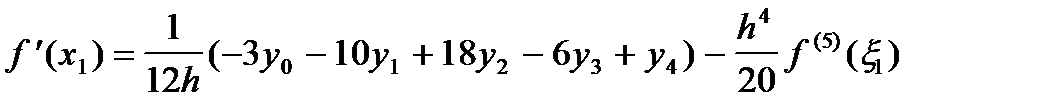;	(18)
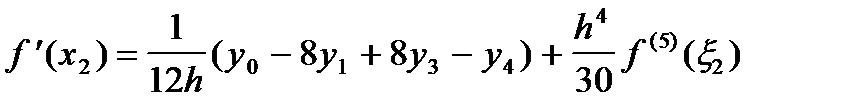;	(19)
;	(20)
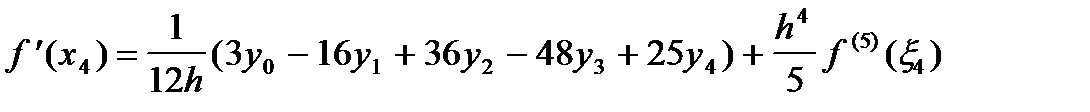.	(21)

Дата добавления: 2014-12-25