Решение. Функция непрерывна на всей числовой оси, следовательно, мы можем воспользоваться теоремой Больцано-Коши

Функция 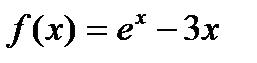непрерывна на всей числовой оси, следовательно, мы можем воспользоваться теоремой Больцано-Коши. Заметим, что при далее а при 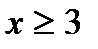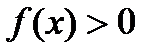. Это означает, что при и при 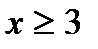данное уравнение не имеет действительных корней. С другой стороны, мы имеем два отрезка: и 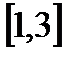, на концах которых непрерывная функция принимает противоположные по знаку значения. Следовательно, на этих отрезках имеется по крайней мере по одному корню.

Рассмотрим теперь первую производную функции 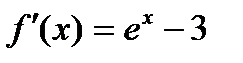. Она сохраняет знак (отрицательна) на отрезке ; следовательно, на этом отрезке уравнение имеет только один корень. На втором отрезке 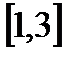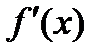знака не сохраняет. Рассмотрим вторую производную . Вторая производная положительна на всей числовой оси, поэтому на отрезке 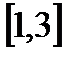- также один корень уравнения.

Задача 2.

Отделить корни уравнения

Дата добавления: 2014-12-25