Итоговый тест

Решение.

По исходным начальным данным x0=1 и y0=2,70 вычисляем 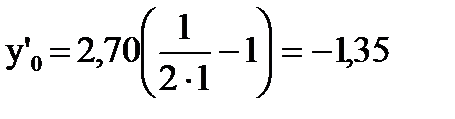. Далее, следуя формуле (4), имеем Dy0=-0,169. Таким образом, по формуле (5) получаем y1=2,70–0,169=2,53.

Дальнейшие вычисления выполняем аналогично, принимая за исходные значения x1,y1; x2,y2 и так далее. Результаты вычислений представлены в следующей таблице.

i	xi	yi	y'i = f(xi,yi)	Dyi = hf(xi,yi)
	1,000	2,70	–1,35	–0,169
	1,125	2,53	–1,41	–0,176
	1,250	2,35	–1,41	–0,176
	1,375	2,17	–1,38	–0,172
	1,500	2,00

Задача Ж.

Решить уравнение y' = f(x,y) на указанном интервале с начальным условием y(x0)=y0, принимая h = 0,1, методом Эйлера

y' = 2x+y;	[0; 0,2];	y0 = 1.
y' = x+2y;	[0; 0,2];	y0 = 1.
y' = x–2y;	[1; 1,2];	y0 = 0.
y' = 2(x+y);	[1; 1,2];	y0 = 0.
y' = 2x–3y;	[1; 1,2];	y0 = 0.
y' = 2x+3y;	[0; 0,2];	y0 = 1.
y' = x+3y;	[0; 0,2];	y0 = 1.
y' = 4x+y;	[0; 0,2];	y0 = 1.
y' = 3x–y;	[0; 0,2];	y0 = 1.
y' = 4x–y;	[0; 0,2];	y0 = 1.

1. Что получится после округления числа 5,785 до сотых долей?

2. Можно ли считать, что число 0,006783 более точное, чем число 6,783? Все знаки верны в узком смысле.

3. Какова оценка относительной погрешности, если вместо числа π взять число α = 3,14? В числе α все знаки верны в узком смысле.

4. Со сколькими десятичными знаками следует взять число α = √18, чтобы относительная погрешность не превышала 0,1%.

5. Сколько верных значащих цифр в числе α = 0,00356 в широком и узком смысле, если ∆α = 0,6 * 10^-5?

6. Приближенное число α = 24534имеет относительную погрешность δα = 1%. Сколько в этом числе верных знаков?

7. Произвести сложение следующих приближенных чисел

u = 0,1732 + 17,45 + 0,000333 + 204,4 + 7,25 + 144,2 + 0,0112 + 0,634 + 0,0771

В каждом из приведенных чисел все значащие цифры в широком смысле.

8. Найти производные приближенных чисел α₁ = 3,6 и α₂ = 84,489. Все написанные знаки верны в широком смысле.

9. Что означает в обратной задаче теории погрешностей принцип равных влияний?

10. В чем состоит задача отделения корней при приближенном решении уравнений f(x) = 0?

11. Какая теория часто используется при отделении корней уравнения f(x) = 0?

12. Может ли алгебраическое уравнение пятой степени иметь ровно два действительных корня?

13. В чем состоит метод половинного деления при уточнении корня уравнения f(x) = 0 на отрезке [a, b]?

14. Можно ли сказать, что метод касательных уточнения корней уравнения f(x) = 0 более точным, чем метод итерации?

15. Почему очень удобно использовать одновременно метод хорд и метод касательных для приближенного решения уравнения f(x) = 0 на интервале изоляции корня?

16. При каких условиях последовательность приближенных значений корня уравнения x = φ(x) на отрезке [a, b], полученная методом итераций, сходится к точному значению корня?

17. Почему полином Лагранжа считают наиболее универсальной формой интерполяционного полинома?

18. Функция f(x) задана таблично в точках х₀, х₁, х₂, х₃, х₄. Можно ли построить полином пятой степени, совпадающий с функцией f(x) в указанных местах?

19. Какова связь разделенной разности f[x₀, x₁….. x_n] и производной f⁽ⁿ⁾(x)?

20. Что можно сказать о разделенных разностях пятого порядка для многочлена четвертой степени?

21. Какова связь конечной разности к – ого порядка и соответствующей производной?

22. Какова связь между погрешностью заданных значений функции в узлах и погрешностью конечных разностей различных порядков.

23. Каким образом анализ таблицы конечных разностей позволяет определить степень интерполяционного полинома?

24. В каком смысле можно считать, что интерполяционные полиномы Стирлинга и Бесселя более точные, чем интерполяционные полиномы Ньютона?

25. Чем отличаются центральные конечные разности от обычных конечных разностей?

26. Почему при решении задачи интерполирования в середине шага таблицы значений функции f(x) применяетс интерполяционный полином Бесселя?

27. Может ли интерполяционный полином стирлинга иметь степень, равную пяти?

28. Может ли интерполяционный полином Бесселя иметь степень, равную четырем?

29. Если шаг таблицы знаячений функции f(x) то, что можно сказатиь об изменении значений конечных разностей различных порядков.

ВЫВОДЫ

Результатом изучения первой части курса «Численные методы» должно явиться, прежде всего, умение грамотно оценивать погрешности результата численного решения задачи, а также четкое понимание связанных с этим особенностей.

При изучении приближенных методов решения уравнений необходимо обратить внимание на границы применимости тех или иных методов, на условиях их сходимости к точечному значению корня, формирование расчетных навыков и оценку возникающих погрешностей.

Изучение теории интерполирования тесно связано с использованием аппарата конечных разностей и выбором соответствующего интерполяционного полинома. Особое место занимает анализ остаточной и вычислительной погрешностей. Это же относиться и к связанным с интерполированием методам численного дифференцирования.

Список литературы

1. Бахвалов Н.С. Численные методы. –М: Наука, 1975.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2001.

3. Березин И.С., Жидков Н.П. Методы вычислений. – Т.1. – М.: Наука, 1966; - Т.2. – М.: Физматгиз, 1962.

4. Волков Е.А. Численные методы. – М.: Наука, 1987.

5. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970.

6. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – М: Наука, 1967.

7. Калиткин Н.Н., Численные методы. - М.: Наука, 1978.

8. Курош А.Г. Курс высшей алгебры. - М.: Наука, 1968.

9. Самарский А.А., Гулин А.В. Численные методы. – М: Наука, 1989.

10. Турчак Л.И. Основы численных методов. – М: Наука, 1987.

11. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. – М: Физматгиз, 1963.

12. Фихтенгольц Г.М. Математический анализ. –Т.1, 2. – М: Гостехиздат, 1957.

Дата добавления: 2014-12-25