
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение систем линейных уравнений
|
|
|
|
Задачи Е1 и Е2.
Точные и приближенные методы. Метод Гаусса с выбором главного элемента. Метод простой итерации.
Современному экономисту приходится решать достаточно большие системы линейных уравнений. Так, при составлении межотраслевого баланса число неизвестных превышает сто. Данная тема посвящена этому актуальному разделу программы.
Все методы решения систем уравнений можно разбить на условно точные и приближенные. К точным алгоритмам относится – метод Крамера, Гаусса, Жордана-Гаусса и т.д. Среди приближенных следует отметить, прежде всего, итерационные методы, метод квадратного корня и т.д.
Контрольная работа предусматривает решение одной системы методом Гаусса с выбором главного элемента и одной системы методом простой итерации. Примеры на эти методы разобраны ниже.
Метод Гаусса с выбором главного элемента.
Запишем систему линейных уравнений следующим образом:
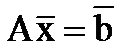 . .
| (1) |
Расширенная матрица A этой системы имеет вид:
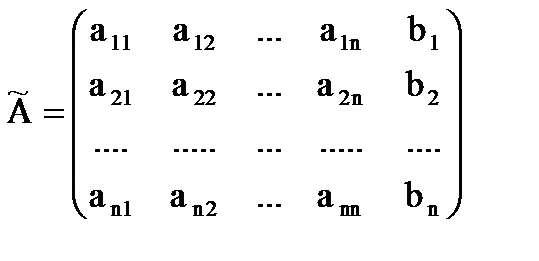
| (2) |
На первом шаге элемент a11¹0 называется ведущим. Разделим на него первую строку матрицы A, в результате получим (3).
 . .
| (3) |
Найдем x1 из (3), подставим его значение во все остальные уравнения
и тем самым исключим x1 из всех уравнений, кроме первого. Взяв теперь полученную систему без первого уравнения, повторяем этот процесс, беря в качестве ведущего элемента коэффициент при x2 и т.д. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-ого) уравнения не останется лишь один член с неизвестным xn, т.е. матрица системы будет приведена к треугольному виду. Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное xn. Далее, используя это значение, из предыдущего уравнения вычисляем xn-1 и т.д. Последним находим x1 из первого уравнения.
|
|
|
Одной из модификаций метода Гаусса является схема с выбором главного элемента. Она состоит в том, что требование akk¹0 (на akk происходит деление в процессе исключения) заменяется более жестким: из всех оставшихся в матрице элементов нужно выбрать наибольший по модулю и представить уравнение так, чтобы этот элемент оказался на месте ведущего элемента akk.
Схему вычислений по методу Гаусса с выбором главного элемента поясняет следующий пример:
2,74x1–1,18x2+3,17x3 = 2,18;
1,12x1+0,83x2–2,16x3 = –1,15;
0,18x1+1,27x2+0,76x3 = 3,23.
Решение ведется в таблице 1.
Выбираем максимальный элемент в столбцах x1, x2 и x3 раздела A (a13=3,17). Заполняем столбец mi раздела A, полученный делением элементов столбца x3 (результат деления берется с обратным знаком) на максимальный элемент a13=3,17:
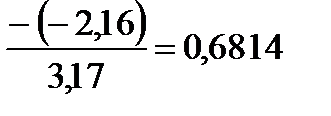 ;
; 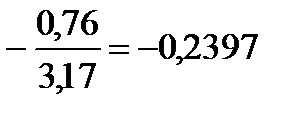 .
.
Таблица 1.
| mi | Коэф-ты при неизвестных | Сво-бодн. члены | å | å¢ | |||
| x1 | x2 | x3 | |||||
| А | –1 0,6814 –0,2397 | 2,74 1,12 0,18 | –1,18 0,83 1,27 | 3,17 –2,16 0,76 | 2,18 –1,15 3,23 | 6,91 –1,36 5,44 | — |
| Б | –1 0,1596 | 2,9870 –0,4768 | 0,0259 1,5528 | — — | 0,3355 2,7075 | 3,3484 3,7835 | 3,3485 3,7837 |
| В | — | — | 1,5569 | — | 2,7601 | 4,3170 | 4,3181 |
В столбец å записываются суммы коэффициентов строк матрицы A:
2,74+(–1,18)+3,17+2,18=6,91;
1,12+0,83+(–2,16)+(–1,15)= –1,36;
0,18+1,27+0,76+3,23=5,44.
Переход к разделу Б ведется следующим образом: строку, содержащую главный (ведущий) элемент, умножаем на mi и прибавляем к соответствующей i-ой строке. Результат записываем в раздел Б. Строка с ведущим элементом в раздел Б не переписывается.
2,74×0,6814+1,12=2,9870;
(–1,18) × 0,6814 +0,83=0,0259;
2,28×0,6814+(–1,15)=0,3355;
6,91×0,6814+(–1,36)=3,3485
(результат заносится в столбец å¢).
Далее считает сумму å в каждой строке раздела Б.
2,9870+0,0259+0,3355=3,3484;
–0,4768+1,5528+2,7075=3,7835.
|
|
|
Если столбцы å и å¢ совпадают (с заданной точностью), то вычисления выполнены верно и можно переходить к следующему шагу: выбираем главный элемент (2,9870), считаем mi и т.д.
В результате обратного хода получаем:
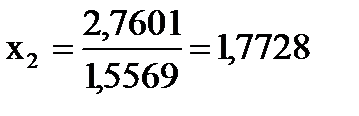 ;
;
 ;
;
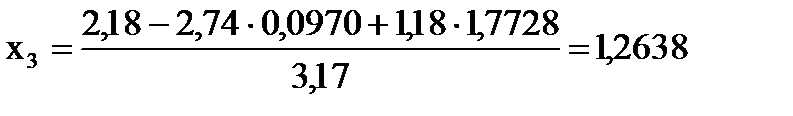 .
.
Практически, вследствие вычислительных погрешностей, полученное методом Гаусса решение системы является приближенным. Покажем, как уточнить это решение.
Пусть для системы

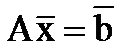
получено приближенное решение 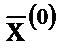 . Положим
. Положим  .
.
Тогда для вектора поправки 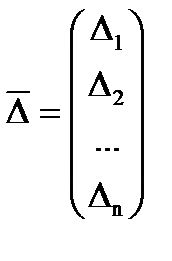 будем иметь уравнение
будем иметь уравнение
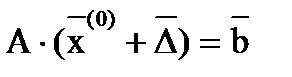
или
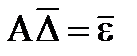 ,
,
где 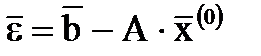 – вектор невязок для приближенного решения
– вектор невязок для приближенного решения 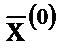 . Таким образом, чтобы найти
. Таким образом, чтобы найти  , нужно решить систему с прежней матрицей A и новым вектором свободных членов
, нужно решить систему с прежней матрицей A и новым вектором свободных членов 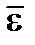 . Заметим, что преобразованные коэффициенты матрицы A можно не уточнять, так как при малых невязках соответствующие ошибки будут иметь более высокий порядок малости.
. Заметим, что преобразованные коэффициенты матрицы A можно не уточнять, так как при малых невязках соответствующие ошибки будут иметь более высокий порядок малости.
Найдем поправку  к полученному в нашем примере решению
к полученному в нашем примере решению
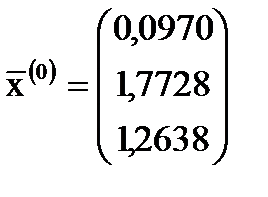 .
.
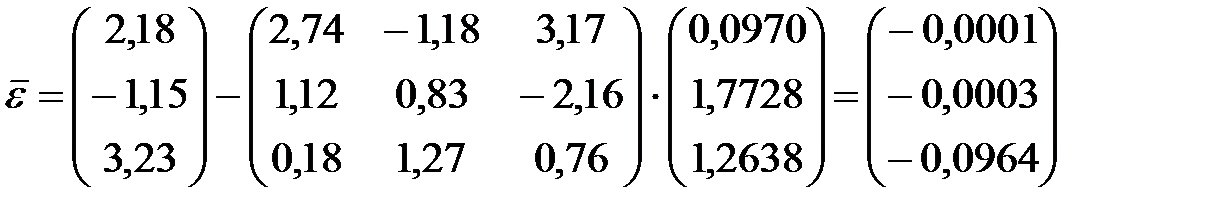 .
.
Коэффициенты при неизвестных D1, D2, D3 уже имеются готовыми в таблице 1. Остается лишь преобразовать вектор свободных членов.
| Прямой ход | Таблица 2. |
| mi | Коэф-ты при неизвестных | Свобод. члены | å | å¢ | |||
| D1 | D2 | D3 | |||||
| А | –1 0,6814 –0,2397 | 2,74 1,12 0,18 | –1,18 0,83 1,27 | 3,17 –2,16 0,76 | –0,0001 –0,0003 –0,0964 | 4,7299 –0,2103 2,1136 | — |
| Б | –1 0,1596 | 2,9870 –0,4768 | 0,0259 1,5528 | — — | –0,0004 –0,0964 | 3,0125 0,9796 | 3,0127 0,9798 |
| В | — | — | 1,5569 | — | –0,0964 | 1,4605 | 1,4604 |
Обратный ход.
D2=  =–0,0619;
=–0,0619;
D1= 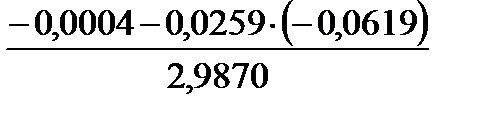 =0,0004;
=0,0004;
D3= 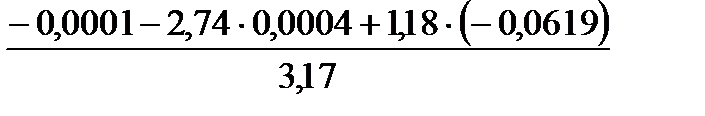 =–0,0234.
=–0,0234.
Вектор  может служить для приближенной оценки абсолютной погрешности полученного решения.
может служить для приближенной оценки абсолютной погрешности полученного решения.
Метод простой итерации.
При большом числе уравнений и неизвестных метод Гаусса мало применим, т.к. его реализация требует слишком большого числа вычислений, а, следовательно, даже при точных исходных данных неизбежно появляются погрешности вычислений, которые будут тем больше, чем больше самих вычислений. Потому для решения больших систем используются итерационные методы, которые обладают следующими преимуществами:
1. Если процесс итерации сходится быстро, т.е. количество приближений меньше, чем порядок системы, то получается выигрыш во времени решения.
2. Метод итераций является самокорректирующимся, т.е. отдельные ошибки не отражаются на конечном результате решения.
|
|
|
3. Процесс итераций легко программируется на ЭВМ.
Ниже рассматривается один из методов итераций – метод простой итерации.
Пусть дана система линейных алгебраических уравнений
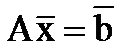 , ,
| (4) |
где A – невырожденная матрица.
Приводя с помощью линейных преобразований эту систему к эквивалентному виду
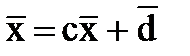 , ,
| (5) |
будем решать последнюю методом последовательных приближений. Взяв за нулевое приближение какой-либо вектор 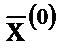 , вычислим приближение
, вычислим приближение 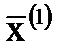 по формуле
по формуле
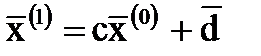 , ,
| (6) |
аналогично
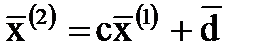 и т.д. и т.д.
| (7) |
Последовательность векторов 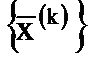 , k=1,2,…, сходится к точному решению
, k=1,2,…, сходится к точному решению 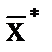 , т.е.
, т.е.
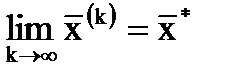 , ,
| (8) |
если норма матрицы c
| ||c|| < 1. | (9) |
Норма ||c|| определяется по одному из следующих способов:
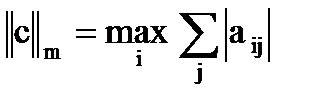 ;
;
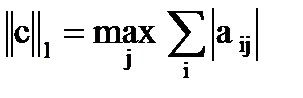 ; ;
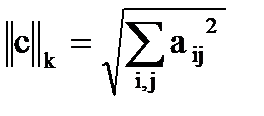 . .
| (10) |
При сделанных предположениях о норме матрицы c погрешность k-ого приближения можно оценить следующим образом:
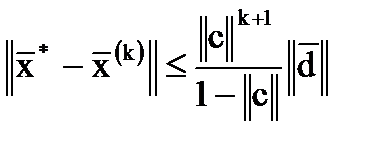 при при 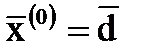 ; ;
| (11) |
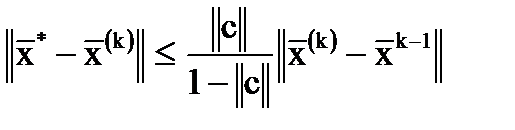 . .
| (12) |
Первая из этих формул позволяет оценить количество итераций, теоретически необходимых для достижения заданной точности.
Пример. Решить систему с точностью до 0,001.
| 4,5x1–1,8x2+3,6x3=–1,7; | (I) |
| 3,1x1+2,3x2–1,2x3=3,6; | (II) |
| 1,8x1+2,5x2+4,6x3=2,2. | (III) |
Приведем систему к виду, в котором элементы главной диагонали превосходили бы сумму модулей остальных элементов строки. Это обеспечит выполнение условия (9): ||c||m < 1.
| 7,6x1+0,5x2+2,4x3=1,9; | (I + II) |
| 2,2x1+9,1x2+4,4x3=9,7; | (2III + II – I) |
| –1,3x1+0,2x2+5,8x3=–1,4. | (III – II) |
Отсюда
10x1=2,4x1–0,5x2–2,4x3+1,9;
10x2=–2,2x1+0,9x2–4,4x3+9,7;
10x3=1,3x1–0,2x2+4,2x3–1,4.
В окончательном виде наша система запишется следующим образом:
x1=0,24x1–0,05x2–0,24x3+0,19;
x2=–0,22x1+0,09x2–0,44x3+0,97;
x3=0,13x1–0,02x2+0,42x3–0,14.
Матрица c и вектор 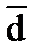 для этой системы будут иметь вид:
для этой системы будут иметь вид:
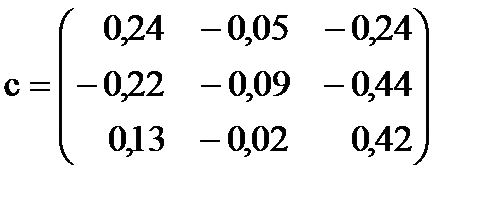 ; ;
| 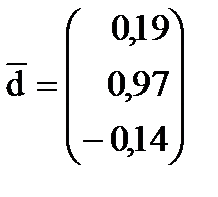 . .
|
Нормы матрицы c, вектора 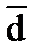 будут соответственно равны:
будут соответственно равны:
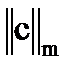 = max(0,24+0,05+0,24; 0,22+0,09+0,44; 0,13+0,02+0,42)=
= max(0,24+0,05+0,24; 0,22+0,09+0,44; 0,13+0,02+0,42)=
= max(0,53; 0,75; 0,67)=0,75<1.
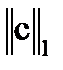 = max(0,24+0,22+0,13; 0,05+0,09+0,02; 0,24+0,44+0,42)=
= max(0,24+0,22+0,13; 0,05+0,09+0,02; 0,24+0,44+0,42)=
= max(0,59; 0,16; 1,10)=1,10>1.
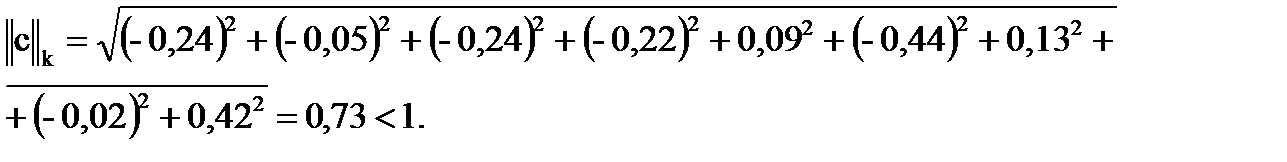
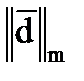 =max(0,19; 0,97; 0,14)=0,97.
=max(0,19; 0,97; 0,14)=0,97.
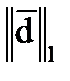 =max(0,19+0,97+0,14)=1,30.
=max(0,19+0,97+0,14)=1,30.
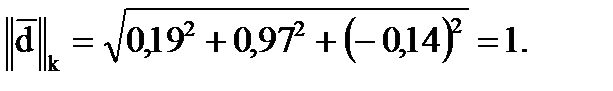
Т.к. 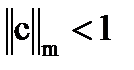 , то процесс итераций сходится, и теоретическое число итераций k будет определяться по формуле:
, то процесс итераций сходится, и теоретическое число итераций k будет определяться по формуле:
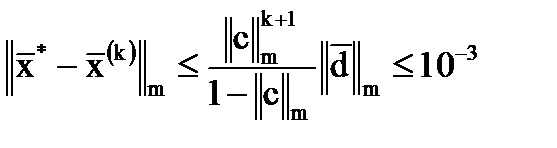 , или
, или
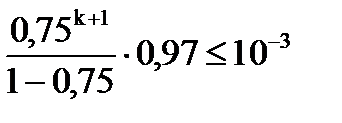 , т.е.
, т.е.
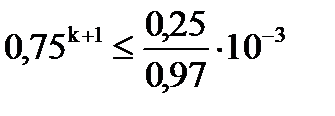
Отсюда k³28.
Теоретическая оценка числа итераций, необходимых для обеспечения заданной точности, практически всегда очень завышена.
|
|
|
Вычисления располагаем в таблице.
| Номер итерации | x1 | x2 | x3 |
| 0,19 | 0,97 | –0,14 | |
| 0,2207 | 1,0703 | –0,1915 | |
| 0,2354 | 1,0988 | –0,2118 | |
| 0,2424 | 1,1088 | –0,2196 | |
| 0,2454 | 1,1124 | –0,2226 | |
| 0,2467 | 1,1138 | –0,2237 | |
| 0,2472 | 1,1143 | –0,2241 | |
| 0,2474 | 1,1145 | –0,2243 |
На 7 итерации имеем, что
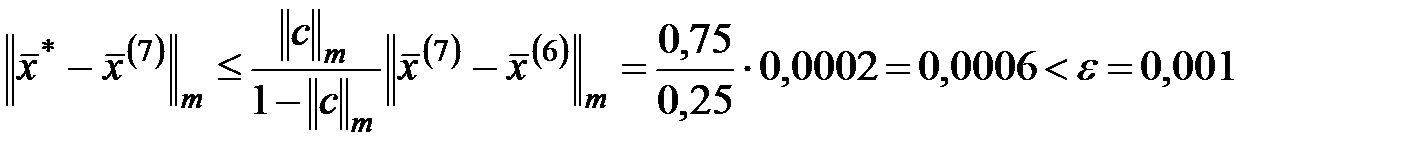 .
.
Следовательно, необходимая точность достигнута.
Ответ: x1=0,2474; x2=1,1145; x3=–0,2243.
Задача Е1.
Решить систему уравнений методом Гаусса с выбором главного элемента. Для полученного решения найти вектор поправок.
| №1. | 0,34x1+0,71x2+0,63x3=2,08; 0,71x1–0,65x2–0,18x3=0,17; 1,17x1–2,35x2+0,75x3=1,28. | №2. | 3,75x1–0,28x2+0,17x3=0,75; 2,11x1–0,11x2–0,12x3=1,11; 0,22x1–3,17x2+1,81x3=0,05. | |
| №3. | 0,21x1–0,18x2+0,75x3=0,11; 0,13x1+0,75x2–0,11x3=2,00; 3,01x1–0,33x2+0,11x3=0,13. | №4. | 0,13x1–0,14x2–2,00x3=0,15; 0,75x1+0,18x2–0,77x3=0,11; 0,28x1–0,17x2+0,39x3=0,12. | |
| №5. | 3,01x1–0,14x2–0,15x3=1,00; 1,11x1+0,13x2–0,75x3=0,13; 0,17x1–2,11x2+0,71x3=0,17. | №6. | 0,92x1–0,83x2+0,62x3=2,15; 0,24x1–0,54x2+0,43x3=0,62; 0,73x1–0,81x2–0,67x3=0,88. | |
| №7. | 1,24x1–0,87x2–3,17x3=0,46; 2,11x1–0,45x2+1,44x3=1,50; 0,48x1+1,25x2–0,63x3=0,35. | №8. | 0,64x1–0,83x2+4,20x3=2,33; 0,58x1–0,83x2+1,43x3=1,71; 0,86x1+0,77x2+0,88x3=0,54. | |
| №9. | 0,32x1–0,42x2+0,85x3=1,32; 0,63x1–1,43x2–0,58x3= –0,44; 0,84x1–2,23x2–0,52x3=0,64. | №10. | 0,73x1+1,24x2–0,38x3=0,58; 1,25x1+0,66x2–0,78x3=0,66; 0,75x1+1,22x2–0,83x3=0,92. | |
| №11. | 0,62x1–0,44x2–0,86x3=0,68; 0,83x1+0,42x2–0,56x3=1,24; 0,58x1–0,37x2–2,62x3=0,87. | №12. | 1,26x1–2,34x2+1,17x3=3,14; 0,75x1+1,24x2–0,48x3= –1,17; 3,44x1+1,85x2+1,16x3=1,83. | |
| №13. | 0,46x1+1,72x2+2,53x3=2,44; 1,53x1–2,32x2–1,83x3=2,83; 0,75x1+0,86x2+3,72x3=1,06. | №14. | 2,47x1+0,65x2–1,88x3=1,24; 1,34x1+1,17x2+2,54x3=2,35; 0,86x1–1,73x2–1,08x3=3,15. | |
| №15. | 4,24x1+2,73x2–1,55x3=1,87; 2,34x1+1,27x2–3,15x3=2,16; 3,05x1–1,05x2–0,03x3= –1,25. |
| №16. | 0,43x1+1,24x2–0,58x3=2,71; 0,74x1+0,83x2+1,17x3=1,26; 1,43x1+1,58x2+0,83x3=1,03. | №17. | 0,43x1+0,63x2+1,14x3=2,18; 1,64x1–0,83x2–2,45x3=1,84; 0,58x1+1,55x2+3,18x3=0,74. | |
| №18. | 1,24x1+0,32x2–0,95x3=1,43; 2,25x1–1,18x2+0,57x3=2,43; 1,72x1–0,83x2+0,57x3=3,88. | №19. | 0,62x1+0,56x2–2,43x3=1,16; 1,32x1–0,88x2+1,76x3=2,07; 0,73x1+1,42x2–0,34x3=2,18. | |
| №20. | 1,06x1+0,34x2+1,26x3=1,17; 2,54x1–1,16x2+0,55x3=2,23; 1,34x1–0,47x2–0,83x3=3,26. | №21. | 3,15x1–1,72x2–1,23x3=2,15; 0,72x1+0,67x2+1,18x3=1,43; 2,57x1–1,34x2–0,68x3=1,03. | |
| №22. | 1,73x1–0,83x2+1,82x3=0,36; 0,27x1+0,53x2–0,64x3=1,23; 0,56x1–0,48x2+1,95x3= –0,76. | №23. | 0,95x1+0,72x2–1,14x3=2,15; 0,63x1+0,24x2+0,38x3=0,72; 1,28x1–1,08x2–1,16x3=0,97. | |
| №24. | 2,18x1+1,72x2–0,93x3=1,06; 1,42x1+0,18x2+1,12x3=2,07; 0,92x1–1,14x2–2,53x3= –0,45. | №25. | 2,18x1+1,72x2–0,93x3=1,06; 1,42x1+0,18x2+1,12x3=2,07; 0,92x1–1,14x2–2,53x3= –0,45. | |
Задача Е2.
Методом простой итерации решить с точностью до 0,001 систему линейных уравнений.
| №1. | 2,7x1+3,3x2+1,3x3=2,1; 3,5x1–1,7x2+2,8x3=1,7; 4,1x1+5,8x2–1,7x3=0,8. | №2. | 1,7x1+2,8x2+1,9x3=0,7; 2,1x1+3,4x2+1,8x3=1,1; 4,2x1–1,7x2+1,3x3=2,8. |
| №3. | 3,1x1+2,8x2+1,9x3=0,2; 1,9x1+3,1x2+2,1x3=2,1; 7,5x1+3,8x2+4,8x3=5,6. | №4. | 9,1x1+5,6x2+7,8x3=9,8; 3,8x1+5,1x2+2,8x3=6,7; 4,1x1+5,7x2+1,2x3=5,8. | ||
| №5. | 3,3x1+2,1x2+2,8x3=0,8; 4,1x1+3,7x2+4,8x3=5,7; 2,7x1+1,8x2+1,1x3=3,2. | №6. | 7,6x1+5,8x2+4,7x3=10,1; 3,8x1+4,1x2+2,7x3=9,7; 2,9x1+2,1x2+3,8x3=7,8. | ||
| №7. | 3,2x1–2,5x2+3,7x3=6,5; 0,5x1+0, 34x2+1,7x3= –0,24; 1,6x1+2,3x2–1,5x3=4,3. | №8. | 5,4x1–2,3x2+3,4x3= –3,5; 4,2x1+1,7x2–2,3x3=2,7; 3,4x1+2,4x2+7,4x3=1,9. | ||
| №9. | 3,6x1+1,8x2–4,7x3=3,8; 2,7x1–3,6x2+1,9x3=0,4; 1,5x1+4,5x2+3,3x3= –1,6. | №10. | 5,6x1+2,7x2–1,7x3=1,9; 3,4x1–3,6x2–6,7x3= –2,4; 0,8x1+1,3x2+3,7x3=1,2. | ||
| №11. | 2,7x1+0,9x2–1,5x3=3,5; 4,5x1–2,8x2+6,7x3=2,6; 5,1x1+3,7x2–1,4x3= –0,14. | №12. | 4,5x1–3,5x2+7,4x3=2,5; 3,1x1–0,6x2–2,3x3= –1,5; 0,8x1+7,4x2–0,5x3=6,4. | ||
| №13. | 3,8x1+6,7x2–1,2x3=5,2; 6,4x1+1,3x2–2,7x3=3,8; 2,4x1–4,5x2+3,5x3= –0,6. | ||||
| №14. | 5,4x1–6,2x2–0,5x3=0,52; 3,4x1+2,3x2+0,8x3= –0,8; 2,4x1–1,1x2+3,8x3=1,8. | №15. | 7,8x1+5,4x2+4,8x3=1,8; 3,3x1+1,1x2+1,8x3=2,3; 4,5x1+3,3x2+2,8x3=3,4. | ||
| №16. | 3,8x1+4,1x2–2,3x3=4,8; –2,1x1+3,9x2–5,8x3=3,3; 1,8x1+1,1x2–2,1x3=5,8. | №17. | 1,7x1–2,2x2+3,0x3=1,8; 2,1x1+1,9x2–2,3x3=2,8; 4,2x1+3,9x2–3,1x3=5,1. | ||
| №18. | 2,8x1+3,8x2–3,2x3=4,5; 2,5x1–2,8x2+3,3x3=7,1; 6,5x1–7,1x2+4,8x3=6,3. | №19. | 3,3x1+3,7x2+4,2x3=5,8; 2,7x1+2,3x2–2,9x3=6,1; 4,1x1+4,8x2–5,0x3=7,0. | ||
| №20. | 7,1x1+6,8x2+6,1x3=7,0; 5,0x1+4,8x2+5,3x3=6,1; 8,2x1+7,8x2+7,1x3=5,8. | №21. | 3,7x1+3,1x2+4,0x3=5,0; 4,1x1+4,5x2–4,8x3=4,9; –2,1x1–3,7x2+1,8x3=2,7. | ||
| №22. | 4,1x1+5,2x2–5,8x3=7,0; 3,8x1–3,1x2+4,0x3=5,3; 7,8x1+5,3x2–6,3x3=5,8. | №23. | 3,7x1–2,3x2+4,5x3=2,4; 2,5x1+4,7x2–7,8x3=3,5; 1,6x1+5,3x2+1,3x3= –2,4. | ||
| №24. | 6,3x1+5,2x2–0,6x3=1,5; 3,4x1–2,3x2+3,4x3=2,7; 0,8x1+1,4x2+3,5x3= –2,3. | №25. | 1,5x1+2,3x2–3,7x3=4,5; 2,8x1+3,4x2+5,8x3= –3,2; 1,2x1+7,3x2–2,3x3=5,6. | ||
Задача Ж.
| Задача 1. | Решить дифференциальное уравнение  с начальным условием y(1)=2,70 на интервале [1; 1,5] методом Эйлера, принимая h=0,125. Все вычисления вести с тремя верными в узком смысле знаками. с начальным условием y(1)=2,70 на интервале [1; 1,5] методом Эйлера, принимая h=0,125. Все вычисления вести с тремя верными в узком смысле знаками.
|
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 1244; Нарушение авторских прав?; Мы поможем в написании вашей работы!