Интерполяционная формула Адамса

При построении интерполяционного многочлена F(x) можно использовать кроме значений 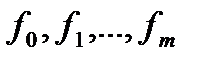еще неизвестное значение 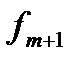. Возьмем в качестве интерполяционного многочлена вторую интерполяционную форму Ньютона, а в качестве начальной точки выбираем

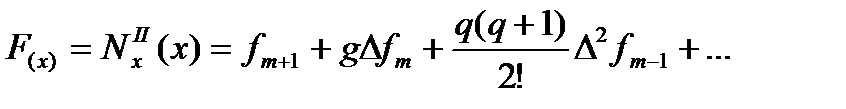(132)

Подставив значение (132) и (113), получаем

(133)

Производя в (133) замену 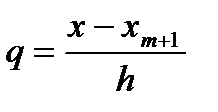, получим:

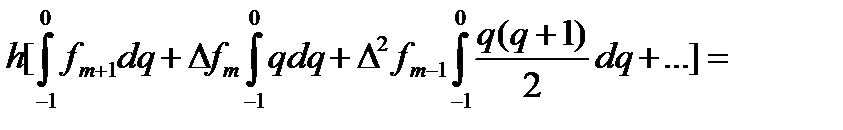(135)

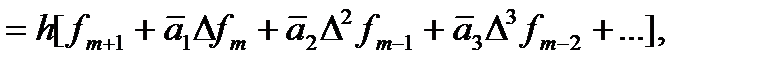
Или, используя обозначения (120),

, (136)

Где

,

,

,

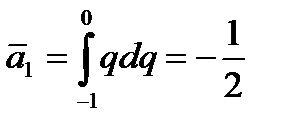, (137)

...............

.

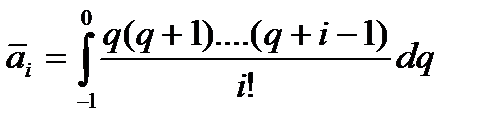Таким образом, формула (135) примет вид:

(138)

Формула (138) называется интерполяционной форсулой Адамса. Поскольку интерполяционная формула Адамса содержит в правой части неизвестное значение:

,

То ее нельзя непосредственно использовать для вычисления значения , она может быть использованна лишь для контроля вычислений, производимых по экстраполяционной формуле Адамса. При этом можно пользоваться той же таблицей, что и для экстраполяционной формулы Адамса. Сначала вычисляются 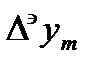и по экстрополяционной формуле Адамса, затем, используя найденное значение 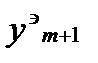, находят: 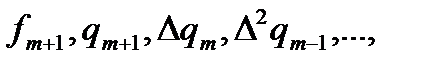затем по интерполяционной формуле определяют значение и .

Оценка Остаточного члена интерполяционной формулы адамса может быть сделана так же, как и для экстраполяционной формулы Адамса. Она имеет вид:

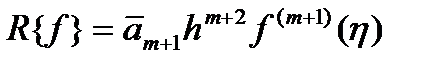. (139)

Т.е. интерполяционная формула Адамса имеет на одном шаге погрешность того же порядка что и экстраполяционная формула адамса (при использовании разностей одного порядка). Однако постоянный множетель в оценке погрешности на шаге интерполяционной формулы Адамса всегда меньше, чем у экстраполяционной формулы того же порядка.

Поэтому интерполяционная формула Адамса точнее экстраполяционной формулы Адамса. Как нетрудно показать, коэффициенты и связаны соотношением

(140)

Причем все и . Откуда ясно, что

(141)

И 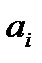- монотонно убывают.

На практике для оценки погрешности значения 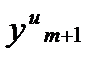, найденного по более точной интерполяциионной формуле Адамса, пользуются следующим приемом. Предположим, что мы использовали экстраполяционную и интерполяционную формулы Адамса до третьих разностей включительно. Тогда, используя выражение для оценки погрешности на шаге, можно записать

(142)

(143)

Вычитая из (142) выражение (143), получим

. (144)

Откуда получаем ошибку более точной интерполяционной формулы Адамса

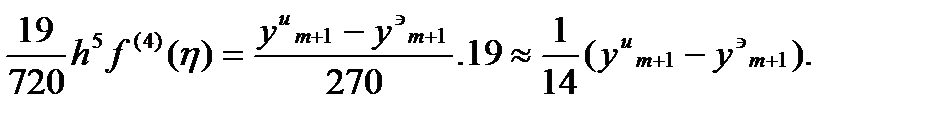(145)

Если 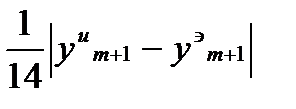не превосходит допустимого значения 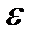, то шаг считается выбранным верно и расчет продолжается с выбранным шагом. Если же на некотором этапе расчета указанная величина превосходит 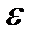, то шаг h следует уменьшить.

Замечание формулы Адамса имеют на одном шаге погрешность порядка , следовательно на всем отрезке погрешность имеет порядок 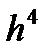. Поэтуму величину h начального шага нужно определять из условия 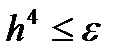. (145)

Пример 12. Найти решение дифферинциального уравнения из примера 11 по интерполяционной формуле адамса. Оценить погрешность полученного решения.

Решение Воспользуемся результатами вычислений и по интерполяционной формуле Адамса. Для этого перепишем первые пять строк таблицы 11 в новую таблицу.

Таблица 12.

x	Y		f(x,y)	q=hf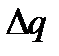
0.0	1.00000		1.00000	0.100000
0.1	1.11034		1.21034	0.121034
0.2	1.24200		1.44280	0.144280
0.3	1.39971	0.183922	1.69971	0.168871
0.4	1.58363	0.183932	1.98363	0.198363
0.4	1.58364	0.213781	1.98364	0.198364
0.5	1.79742	0.213781	2.29742	0.229742
0.5	1.79743	0.213791

Используя найденное значение формулы 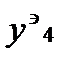, вычисли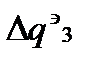м , , , , затем по интерполяционной формуле Адамса вычислим :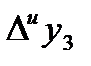

И запишем его в столбец . Вычислим значение искомого решения при еще раз.

=1,39971+0,183932=1,583642

В таблицу 12 еще раз записываем значение 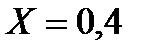и .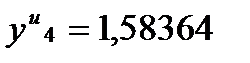

По формуле (145) оцениваем погрешность полученного по более точной, интерполяционной формуле, значения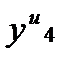

.

Таким образом, полученное значение имеет пять верных знаков после запятой. Поскольку погрешность не превосходит заданного в примере 12 , то дальнейшие вычисления производят с тем же шагом, причем в вычислениях используют значение 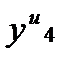, найденное по интерполяционной формуле.

Заново вычисляя , , , , 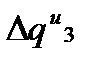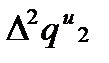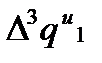Заносим результаты в таблицу 12. Затем по экстраполяционной формуле Адамса вычисляют:

Результаты заносят в таблицу в строку при . После чего вычисляют 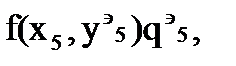, , . По интерполяционной формуле Адамса еще раз находят 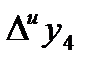и .

.

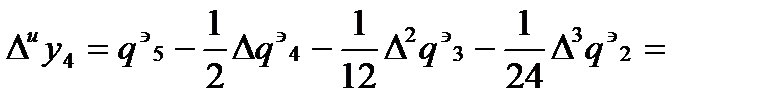
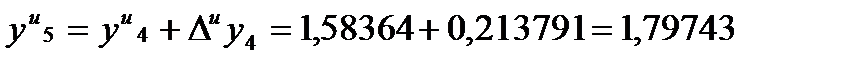Результаты фиксируют в таблице 12, записывая еще раз Х=0,5

Погрешность полученного решения на основании формулы (145) оценивается величиной

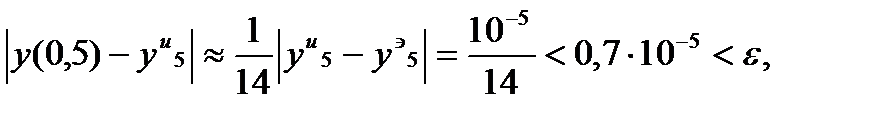
Следовательно процесс нахождения следующего значения 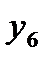можно производить с тем же шагом .

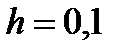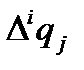Для работы на ЭВМ формулы Адамса удобнее применять в другой форме, выражая значение не через разность , а непосредственно через величины .

Для экстраполяционной формулы Адамса получим:

(146)

.

Если ограничиться одним членом правой части, то получим форму эйлера

. (147)

Два члена правой части дадут

. (148)

Три члена дадут формулу

. (149)

Четыре члена правой части приведут к выражению.

. (150)

Аналогично для интерполяционной формулы Адамса

(151)

(152)

(153)

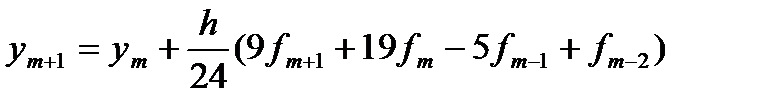(154)

Дата добавления: 2014-12-25