
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод расчетных формул Рунге-Кутта
|
|
|
|
Как уже было показано, решение задачи Коши (1),(2) может быть записанов виде ряда Тейлора (7) или (8), причем все производные, входящие в (8), могут быть фактически вычислены на основании (9). Но в связи с тем, что формулы (9) для вычисления производных очень громоздки, их непосредственное использование на практике весьма затруднительно.
Рунге предложил вместо этого вычислять при помощи линейной комбинации
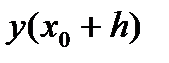
 , (27)
, (27)
где Pi-постоянные коэффициенты;
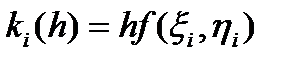 , (28)
, (28)
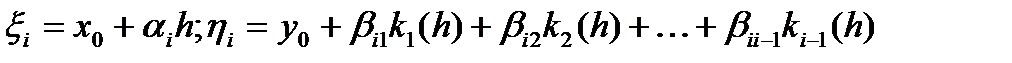 , (29)
, (29)
и a i, b ij – постоянные, а1=0
Расписывая последовательно формулы (28), (29) получаем
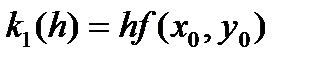 ,
,
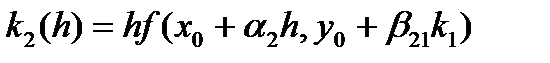 ,
,
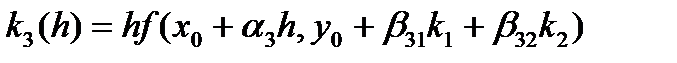 , (30)
, (30)
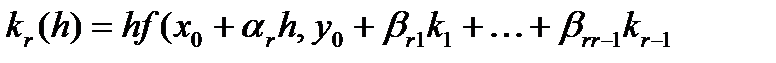 ).
).
Зная a i, b ij для заданного значения h можем вычислить последовательно все ki, а затем 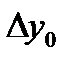 и продвинуться на один шаг, найдя
и продвинуться на один шаг, найдя 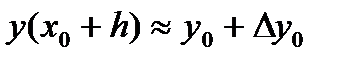 . Выбор постоянных Pi, a i, b ij производится так, чтобы разложения (8) и (27) по степеням h совпадали бы до возможно более высоких степеней h при произвольной функции f(x,y) и произвольном шаге h.
. Выбор постоянных Pi, a i, b ij производится так, чтобы разложения (8) и (27) по степеням h совпадали бы до возможно более высоких степеней h при произвольной функции f(x,y) и произвольном шаге h.
Рассмотрим вопрос о выборе параметров Pi, a i, b ij. Обозначим через
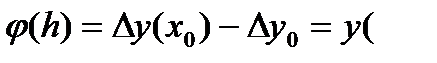
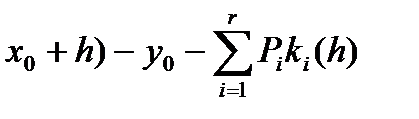 . (31)
. (31)
В силу нашего предположения о совпадении разложений (8) и (27) будем иметь, что
 , (32)
, (32)
т.е. согласно формуле Тейлора
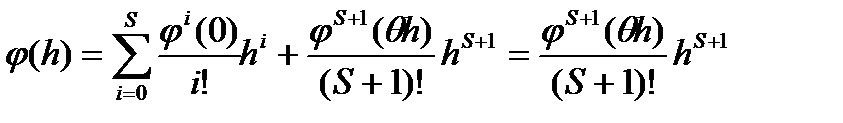 , (33)
, (33)
где 0<q<1.
Мы должны подобрать Pi, a i, b ij так, чтобы S было возможно большим для произвольных f(x,y) и k. Величина j(h) называется погрешностью метода Рунге-Кутта на одном шаге, а S+1 -порядком погрешности метода. Таким образом, разность между точным значением 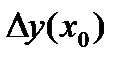 при продвижении на один шаг h и приближенным его значением, вычисленным по формуле (27),т.е. погрешность метода Рунге-Кутта на одном шаге будет равна
при продвижении на один шаг h и приближенным его значением, вычисленным по формуле (27),т.е. погрешность метода Рунге-Кутта на одном шаге будет равна
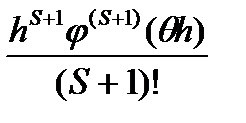 .
.
Очевидно, что условие j(0)=0 будет выполнено всегда, так как ki(0)=0
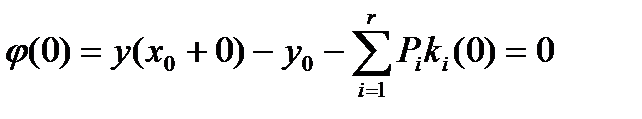 . (34)
. (34)
Рассмотрим метод Рунге-Кутта для различных значений r.
I .k= 1
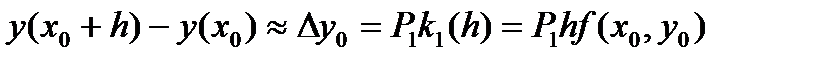 . (35)
. (35)
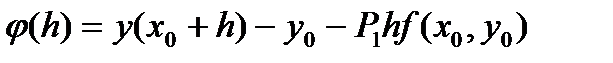 , (36)
, (36)
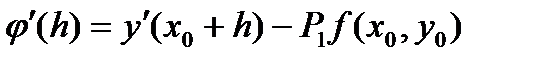 , (37)
, (37)
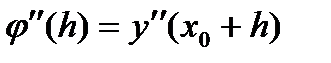 .
.
При h=0
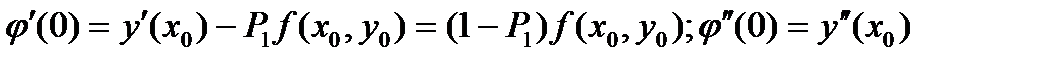 . (38)
. (38)
Очевидно, что равенство 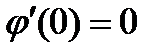 выполняется для всех f(x,y) лишь в случае
выполняется для всех f(x,y) лишь в случае 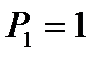 . Далее очевидно, что
. Далее очевидно, что 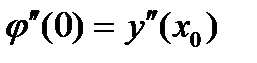 в общем случае нулю не равно.
в общем случае нулю не равно.
Таким образом, при r=1 получим формулу Эйлера:
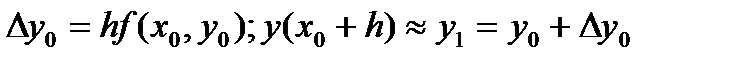 . (39)
. (39)
Для погрешности метода Эйлера на одном шаге получаем выражение
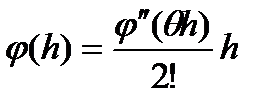
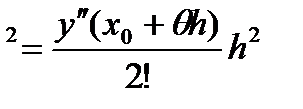 . (40)
. (40)
II.r=2
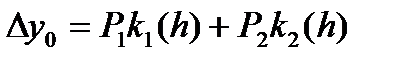 , (41)
, (41)
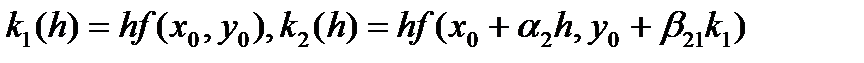 , (42)
, (42)
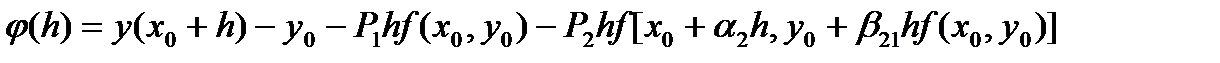 . (43)
. (43)
Вычислим производные функции j(h)
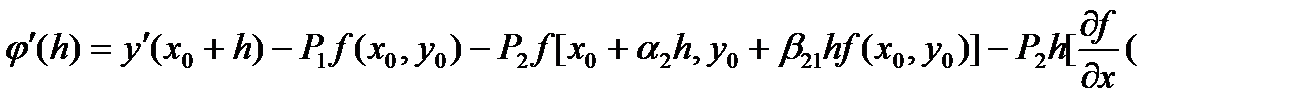
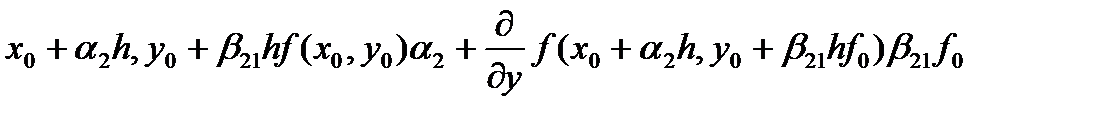 ], (44)
], (44)
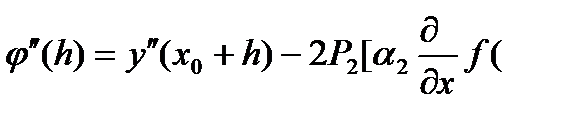
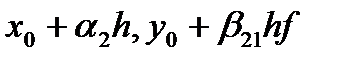
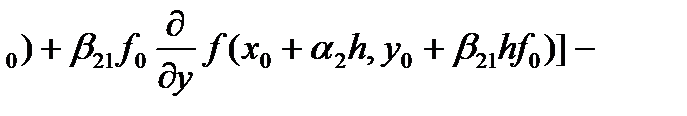
 , (45)
, (45)
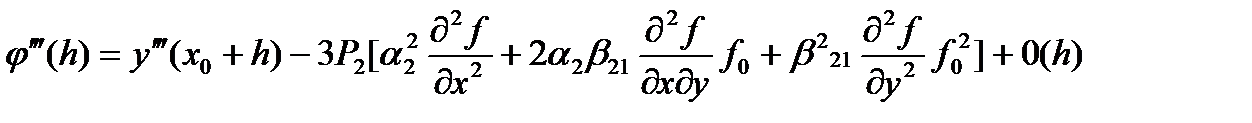 . (46)
. (46)
Согласно исходному уравнению
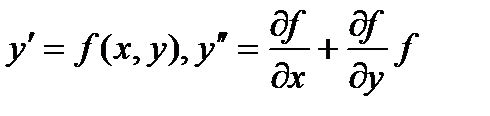 ,
,
 . (47)
. (47)
Используя (47), вычисляем 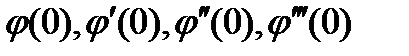 .
.
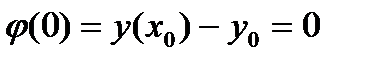 , (48)
, (48)
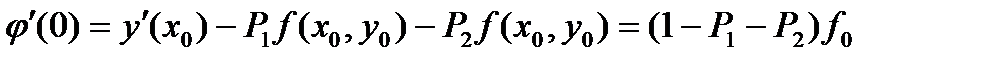 , (49)
, (49)
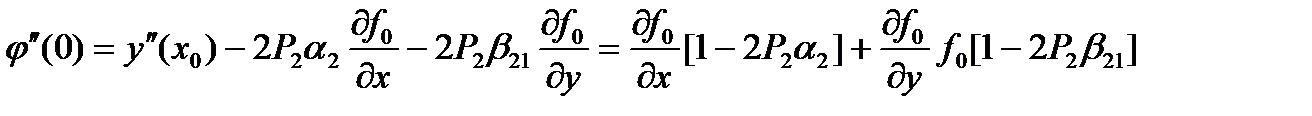 , (50)
, (50)
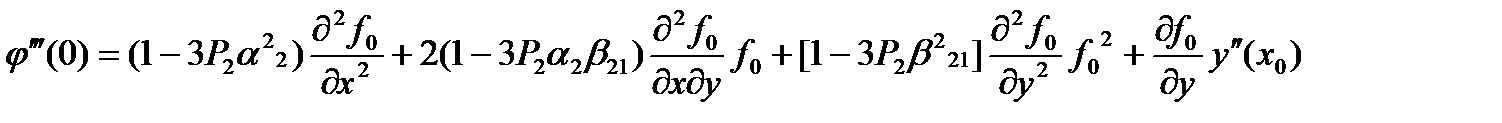 (51)
(51)
Соотношение 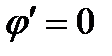 выполняется для всех f(x,y), если
выполняется для всех f(x,y), если 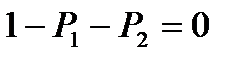 .
.
Соотношение 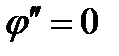 выполняется для всех f(x,y), если
выполняется для всех f(x,y), если 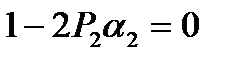 и
и 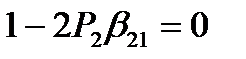 .
.
Очевидно, что 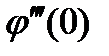 в общем случае нулю не равна, т.е. для r=2 совпадение формул (8) и (27) возможно только до вторых степеней h включительно.
в общем случае нулю не равна, т.е. для r=2 совпадение формул (8) и (27) возможно только до вторых степеней h включительно.
Таким образом, для четырех параметров 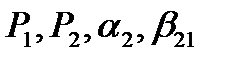 имеем систему из трех уравнений
имеем систему из трех уравнений
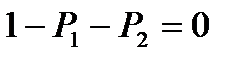
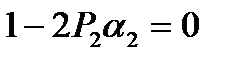 (52)
(52)
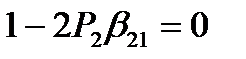 .
.
Система (52) имеет бесчисленное множество решений. Произвольно задавая один из параметров и вычисляя остальные на основании (52), получим различные формулы Рунге-Кутта, имеющие порядок ошибки S+1=3 (на одном шаге)
На практике следует выбирать такие решения (52), которые дают более удобные с точки зрения вычислений формулы.
Для полученных при r=2 формул погрешность на одном шаге имеет выражение
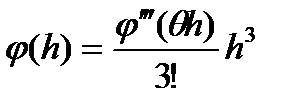 . (53)
. (53)
Рассмотрим некоторые из формул (41), беря различные значения (52). Например, при
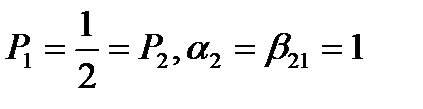 получим формулы
получим формулы
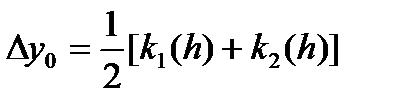 ,
,
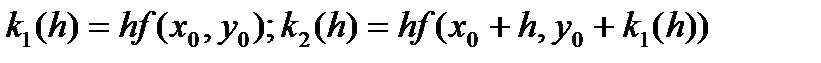 ,
,
или
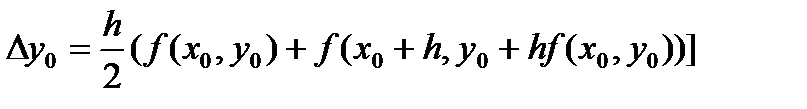 . (54)
. (54)
Если обозначить 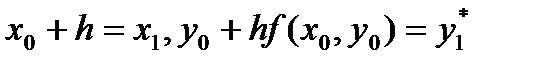 , то получим формулы метода Эйлера-Коши:
, то получим формулы метода Эйлера-Коши:

Если положить 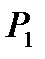 =0, то на основании (52) будем иметь:
=0, то на основании (52) будем иметь:
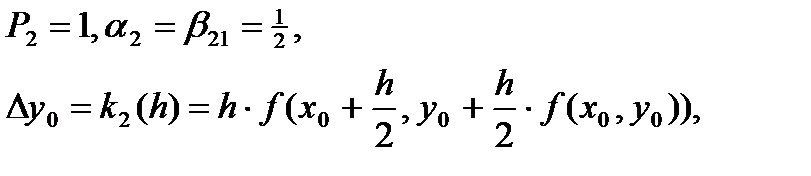 (55)
(55)
что соответствует паре расчётных формул (26) уточнённого метода Эйлера
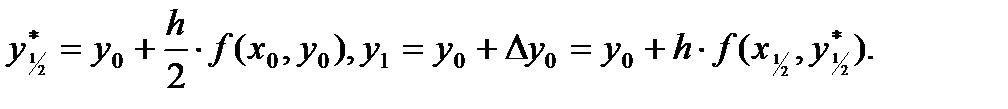
Если положить 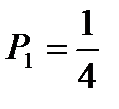 и
и 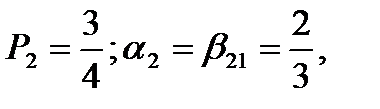
то получим расчётные формулы:
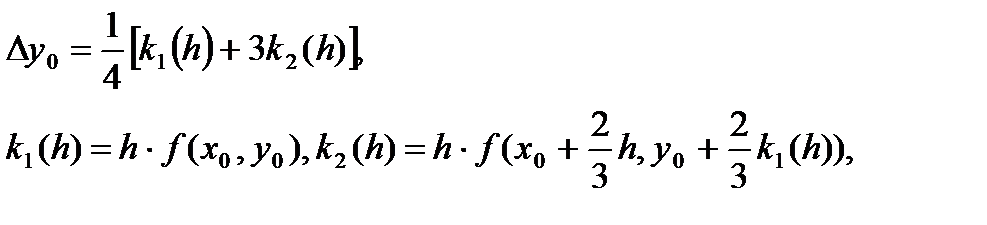 (56)
(56)
причём
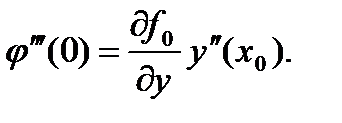 (57)
(57)
 Рассмотрим случай
Рассмотрим случай 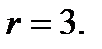 В этом случае (58)
В этом случае (58)
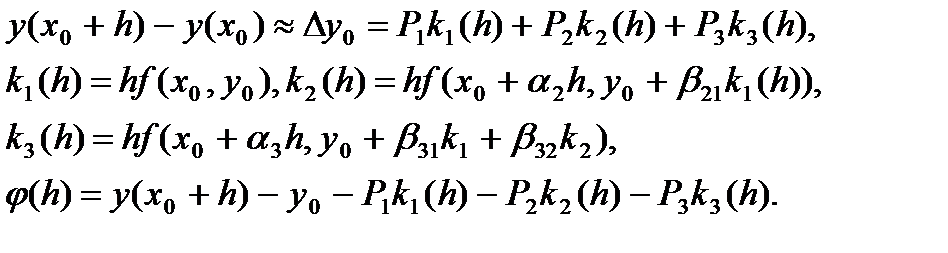 (59) (60)
(59) (60)
В случае 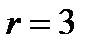 удаётся обратить в нуль только производные
удаётся обратить в нуль только производные
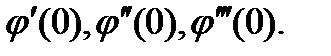 Четвёртая производная
Четвёртая производная 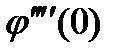 в общем случае нулю не равняется.
в общем случае нулю не равняется.
Поэтому при r=3, S=3, т.е. порядок погрешности расчётной формулы (58) будет 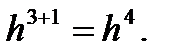
Расчётных формул (58) при S=4  не существует. Чтобы S=3, т.е. равнялись нулю
не существует. Чтобы S=3, т.е. равнялись нулю 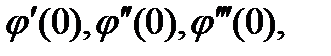 необходимо и достаточно выполнение следующих соотношений:
необходимо и достаточно выполнение следующих соотношений:
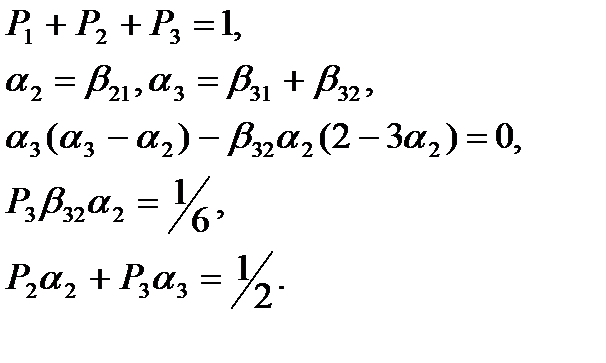 (61)
(61)
Эта система шести уравнений с восьмью неизвестными имеет бесчисленное множество решений. Выбирая в качестве величин 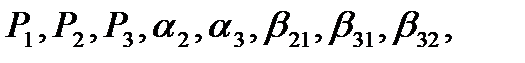 входящих в формулу (61)б получим расчётные формулы Рунге-Кутта, с порядком погрешности на одном
входящих в формулу (61)б получим расчётные формулы Рунге-Кутта, с порядком погрешности на одном
шаге 
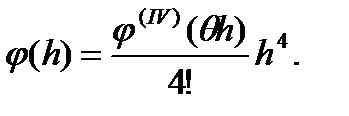 (62)
(62)
Рассмотрим наиболее употребительные из формул (58)
а). Пусть 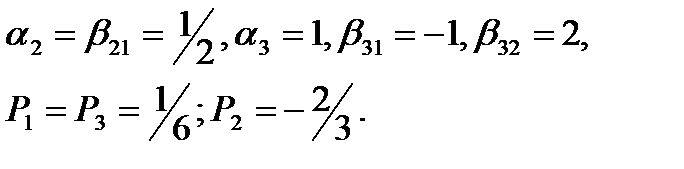
 (63)
(63)
Соответствующая расчётная формула имеет вид:
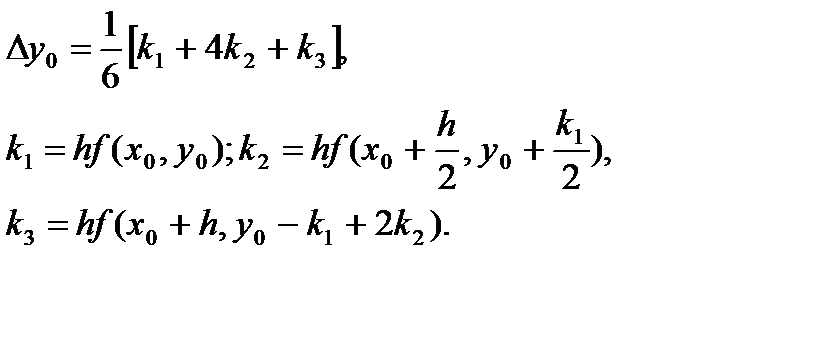 (64)
(64)
(65)
Пусть
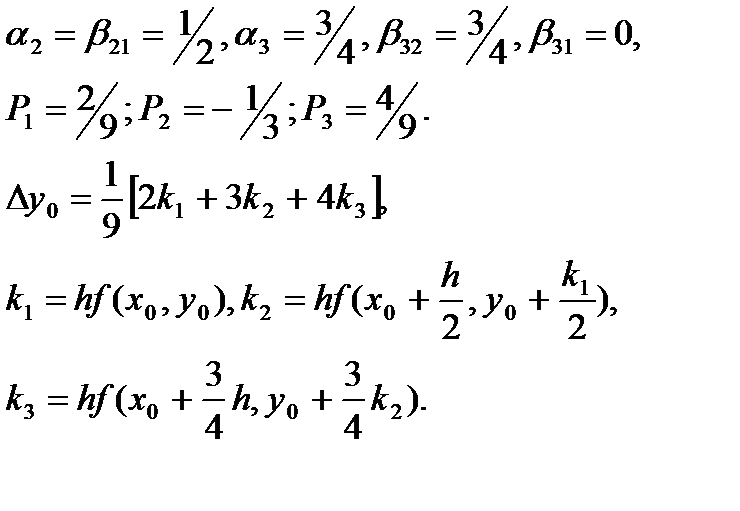 (66)
(66)
IV. Рассмотрим случай 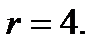 В этом случае (67)
В этом случае (67)
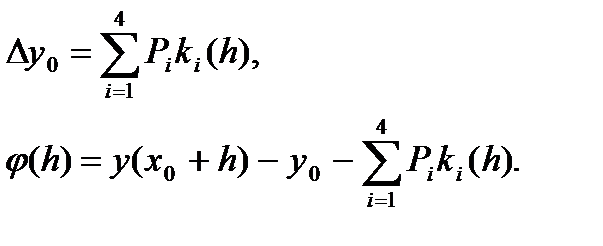 (68)
(68)
При 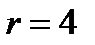 можно построить расчётные формулы с S=4, но не удаётся построить формулы с S=5. Постоянные коэффициенты
можно построить расчётные формулы с S=4, но не удаётся построить формулы с S=5. Постоянные коэффициенты 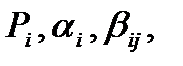 входящие в формулу (67), удовлетворяют системе из 11 уравнений с 13 неизвестными, которые получаются приравниваем нулю производных
входящие в формулу (67), удовлетворяют системе из 11 уравнений с 13 неизвестными, которые получаются приравниваем нулю производных 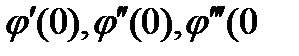 ),
), 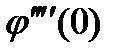 .
.
Выбирая в качестве постоянных коэффициентов решения полученной системы уравнений,
Получим расчетные формулы Рунге-Кутта, имеющие порядок погрешности на шаге 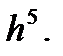
Рассмотрим некоторые частные случаи формул Рунге-Кутта при r=4.
а). Положим
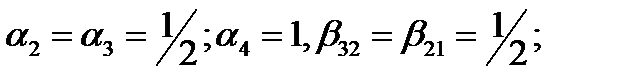
 (69)
(69)
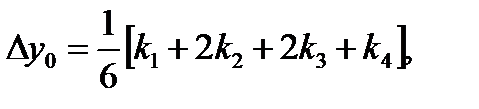
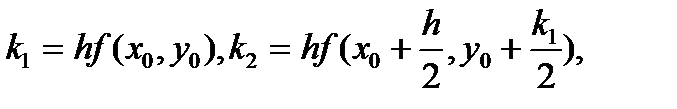 (70)
(70)
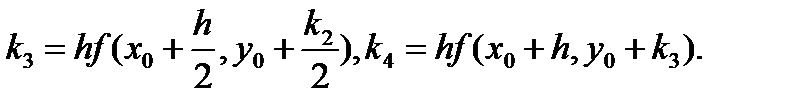 (71)
(71)
Расчётная формула (70) наиболее распространена в вычислительной практике, - формула Рунге-Кутта.
б). 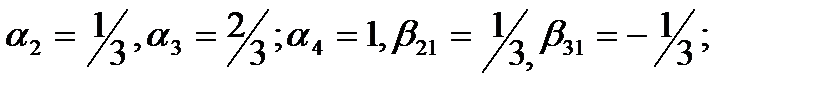
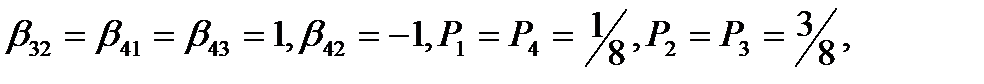 (72)
(72)
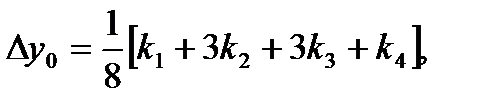
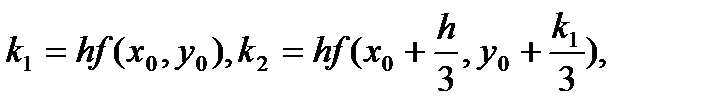 (73)
(73)
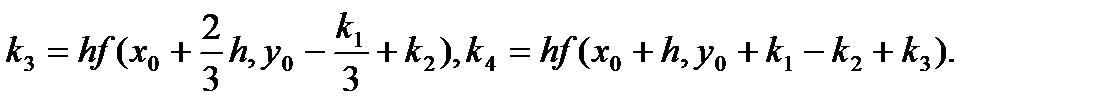 (74)
(74)
Погрешность каждой из формул Рунге-Кутта при r = 4 равна
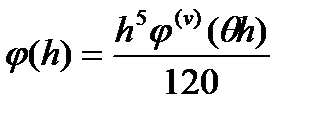 . (75)
. (75)
Как показывают вычисления, при r = 5 не удаётся построить расчётные формулы даже с S =5, т.е., увеличивая r, мы не достигаем увеличения порядка точности. Поэтому эти формулы применения не находят.
Применяя ту или иную формулы Рунге-Кутта, мы найдём значение
 и, следовательно,
и, следовательно, 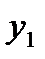 (76)
(76)
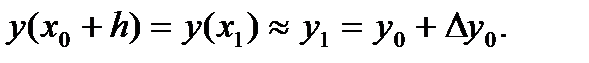
Затем можно взять за начальную точку 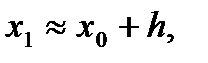 а за начальное значение
а за начальное значение 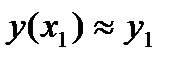
и придвинуться на ещё один шаг такой же или другой длины. Повторяя этот процесс, мы получим таблицу значений искомого решения в некоторых точках.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 2798; Нарушение авторских прав?; Мы поможем в написании вашей работы!