Молекулярная физика и термодинамика. Учебные материалы по разделам курса физики

Учебные материалы по разделам курса физики

2.1 Физические основы классической механики

2.1.1 Основные формулы. Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x

,

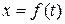где x – некоторая функция времени.

Проекция средней скорости на ось x

Модуль средней скорости

,

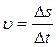где Δ s – путь, пройденный точкой за интервал времени Δ t.

Путь Δ s в отличие от разности координат Δ x = x ₂ – x ₁ не может убывать и принимать отрицательные значения, т. е. Δ s 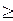0. Тогда проекция мгновенной скорости на ось x

.

Проекция среднего ускорения на ось x

.

Проекция мгновенного ускорения на ось x

.

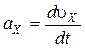Кинематическое уравнение движения точки по окружности

φ = f(t); r = R = const.

Модуль угловой скорости

.

Модуль углового ускорения

.

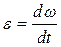Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

; a _τ = ε R; a_n = ω² R,

где 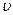– модуль линейной скорости;

a _τ и a_n – модули тангенциального и нормального ускорений;

ω – модуль угловой скорости;

ε – модуль углового ускорения;

R – радиус окружности.

Модуль полного ускорения

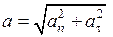или .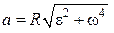

Угол между полным 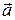и нормальным 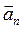ускорениями

α = arccos(a_n / a).

Импульс материальной точки массой m, движущейся со скоростью ,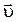

.

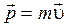Второй закон Ньютона

,

где – результирующая сила, действующая на материальную точку.

Силы, рассматриваемые в механике:

– сила упругости

,

где k – коэффициент упругости (в случае пружины – жесткость);

D 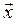– абсолютная деформация;

– сила гравитационного взаимодействия

F = γ ,

где γ – гравитационная постоянная;

m ₁ и m ₂ – массы взаимодействующих тел;

r – расстояние между телами (тела рассматриваются как материальные точки);

– сила тяжести

,

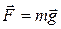где g – ускорение свободного падения.

В случае гравитационного притяжения тела массой к Земле

,

где М и R – масса и радиус Земли соответственно;

– сила трения (скольжения)

F = μ N,

где μ – коэффициент трения;

N – сила нормального давления.

Закон сохранения импульса

,

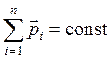или для двух тел (i = 2)

,

где и – скорости тел в момент времени, принятый за начальный;

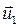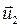и – скорости тех же тел в момент времени, принятый за конечный.

Кинетическая энергия тела, движущегося поступательно,

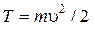
или

T = p ²/2 m.

Потенциальная энергия:

– упругодеформированной пружины

П = k x ²/2,

где k – жесткость пружины;

x – абсолютная деформация;

– гравитационного взаимодействия

,

где γ – гравитационная постоянная;

m ₁ и m ₂ – массы взаимодействующих тел;

r – расстояние между ними (тела рассматриваются как материальные точки);

– тела, находящегося в однородном поле силы тяжести,

П = mgh,

где g – ускорение свободного падения;

h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h «R, здесь R – радиус Земли).

Закон сохранения механической энергии

E = T + П = const.

Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:

А = T = T ₂ – T ₁.

Основное уравнение динамики вращательного движения относительно неподвижной оси z

,

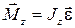где 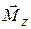– результирующий момент внешних сил относительно оси z, действующих на тело;

– угловое ускорение;

J _z – момент инерции относительно оси вращения.

Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

– стержня длиной L относительно оси, перпендикулярной стержню,

;

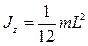– обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),

J _z = m R ²,

где R – радиус обруча (цилиндра);

– диска радиусом R относительно оси, перпендикулярной плоскости диска,

.

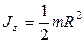Проекция на ось z момента импульса тел, вращающихся относительно неподвижной оси z,

L _z = J ω,

где ω – угловая скорость тела.

Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z,

J _z 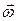= const,

где J _z – момент инерции системы тел относительно оси z;

– угловая скорость вращения тел системы вокруг оси z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,

T =

или

T = L _z²/(2 J _z).

Кинетическая энергия релятивистской частицы

T = (m – m₀)c ² или .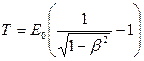

Импульс релятивистской частицы

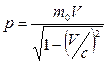или .

Связь между полной энергией и импульсом релятивистской частицы

E ² = E ₀² +(pc)²,

где E ₀ – энергия покоя частицы, E ₀ = m ₀ c ².

Релятивистская масса

или ,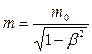

где m ₀ – масса покоя частицы;

V – скорость частицы;

c – скорость света в вакууме;

β – скорость частицы, выраженная в долях скорости света, β = V/c.

Взаимосвязь массы и энергии релятивистской частицы

E = mc ² или .

Полная энергия свободной частицы

E = E ₀ + T,

где T – кинетическая энергия релятивистской частицы.

2.1.2 Примеры решения задач.

Пример 1 – Уравнение движения материальной точки вдоль оси имеет вид x = A + Bt + Ct ³, где A = 2 м, B = 1 м/с, C = – 0,5 м/с³. Найти координату x, скорость V_x и ускорение а_х точки в момент времени t = 2 с.

Дано:	Решение
x = A + Bt + Ct ^3 A = 2 м B = 1 м/с C = – 0,5 м/с^3 t = 2 с	Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В и С и времени t: х = (2 + 1·2 – 0,5·2^3) = 0. Мгновенная скорость относительно оси х есть первая производная от координаты по времени: .
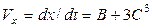x –? Vx –? ах –?

Ускорение точки найдем, взяв первую производную от скорости по времени:

.

В момент времени t = 2 с

V_x = 1 – 3·0,5·2 ² = – 5 м/с; а_х = 6 (– 0,5)·2 = – 6 м/с².

Пример 2 – Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты вращения n ₁ = 480 мин^-1 и предоставлен сам себе. Под действием сил трения маховик остановился через t = 50 с. Найти момент М сил трения.

Дано:	Решение
R = 0,2 м m = 50 кг n 1 = 480 мин^-1= 8 с^-1 t = 50 с	Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде dL Z = M Z dt,
M –?

где dL _Z – изменение проекции на ось Z момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени dt; M _Z – момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно оси Z.

Момент сил трения можно считать не изменяющимся с течением времени (М _Z = const), поэтому интегрирование уравнения приводит к выражению

L _Z = M _Z t.

При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса

L _Z = J _Z ω,

где J _Z – момент инерции маховика относительно оси Z;

ω – изменение угловой скорости маховика.

Приравняв правые части двух предыдущих равенств, получим M _Z t = J _Z ω, откуда

.

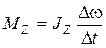Момент инерции маховика в виде сплошного диска определяется по формуле

J _Z = 1/2 mR ².

Изменение угловой скорости ω = ω₂ – ω₁ выразим через конечную n ₂ и начальную n ₁ частоты вращения, пользуясь соотношением ω = 2π n;

ω = ω₂ – ω₁ = 2π n ₂ – 2π n ₁ = 2π(n ₂ – n ₁).

Подставив в формулу для M _Z выражения J _Z и ω, получим

M _Z = π m R²(n ₂ – n ₁) / t.

Проверим, дает ли расчетная формула единицу момента силы. Для этого в правую часть формулы вместо символов величин подставим их единицы:

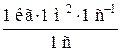= = 1 кг·м·с^-2·1 м = 1 Н·м.

Подставляем численные значения и производим вычисления

M _Z = 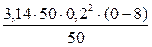= – 1 Н·м.

Знак минус «–» показывает, что момент сил трения оказывает на маховик тормозящее действие.

Пример 3 – Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости V ₁, сообщенной ракете при запуске, она удалится на расстояние, равное радиусу Земли (R = 6,37·10⁶ м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.

Дано:	Решение
R = 6,37·10^6 м	Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При нера ботающем двигателе под действием потенциальной
V 1 –?

силы механическая энергия ракеты изменяться не будет. Следовательно,

Т ₁ + П ₁ = Т ₂ + П ₂,

где Т ₁, П ₁ и Т ₂, П ₂ – кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях.

Согласно определению кинетической энергии

Т ₁ = mV ₁²/2.

Потенциальная энергия ракеты в начальном состоянии

П ₁ = –γ mM / R

(потенциальная энергия гравитационного взаимодействия тел, бесконечно удаленных друг от друга, принимается равной нулю).

По мере удаления ракеты от поверхности Земли ее потенциальная энергия возрастает, а кинетическая – убывает. В конечном состоянии кинетическая энергия Т ₂ станет равной нулю, а потенциальная – достигнет максимального значения

П ₂ = – γ mM /(2 R).

Подставляя выражения Т ₁, П ₁, Т ₂, П ₂ в первоначальную формулу, получаем

mV ₁²/2 – γ mM / R = – γ mM /(2 R),

откуда

V ₁ = .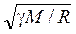

Учитывая, что γ M / R ² = g (g – ускорение свободного падения у поверхности Земли), перепишем эту формулу в виде

V ₁ = ,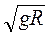

что совпадает с выражением для первой космической скорости.

Произведем вычисления:

V₁ = 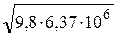= 7,9 км/с.

Пример 4 – Определить импульс p и кинетическую энергию Т электрона, движущегося со скоростью V = 0,9с, где с – скорость света в вакууме.

Дано:	Решение
V = 0,9 с m 0 = 9,1·10^-31кг	Импульсом частицы называется произведение массы частицы на ее скорость
T –? p –?

p = mV.

Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле

,

где m – масса движущейся частицы;

m ₀ – масса покоящейся частицы;

β = V/c – скорость частицы, выраженная в долях скорости света.

Заменив в первом выражении m через m₀ и приняв во внимание, что V = βc, получим выражение для релятивистского импульса:

.

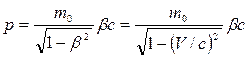В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией Е и энергией покоя Е ₀ этой частицы, т. е. Т = Е – Е ₀. Так как E = mc ² и E₀ = m₀c ², то, учитывая зависимость массы от скорости, получаем

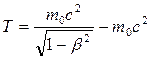или .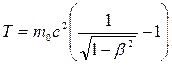

Произведем вычисления:

p =

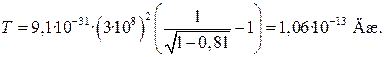
2.2.1 Основные формулы. Количество вещества тела (системы)

ν = N/N _A,

где N – число структурных элементов (молекул, атомов, ионов и т. п.), составляющих тело (систему);

N _A – постоянная Авогадро, N _A = 6,02·10²³ моль^-1.

Молярная масса вещества

μ = m /ν,

где m – масса однородного тела (системы);

ν – количество вещества этого тела.

Количество вещества смеси газов

ν = ν₁ + ν₂ +... + ν_n = N ₁/ N _A + N ₂ / N _A +... + N _n / N _A,

или

ν = m ₁/μ₁ + m ₂/μ₂ +...+ m_n /μ _n,

где ν _i, N_i, m_i, μ _i – количество вещества, число молекул, масса, молярная масса i -го компонента смеси соответственно.

Уравнение Менделеева–Клапейрона (уравнение состояния идеального газа)

pV = νRT = RT,

где m – масса газа;

μ – молярная масса газа;

R – молярная газовая постоянная, R = 8,31 Дж/(моль·К);

ν – количество вещества;

T – термодинамическая температура.

Опытные газовые законы, являющиеся частными случаями уравнения Менделеева–Клапейрона для изопроцессов:

– закон Бойля–Мариотта (изотермический процесс: T = const, m = const)

pV = const

или для двух состояний газа

p ₁ V ₁ = p ₂ V ₂;

– закон Гей-Люссака (изобарный процесс: p = const, m = const)

= const

или для двух состояний газа

;

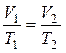– закон Шарля (изохорный процесс: V = const, m = const)

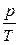= const

или для двух состояний

;

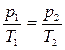– объединенный газовый закон (m = const)

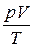= const или ,

где p ₁, V ₁, T ₁ – давление, объем и температура газа в начальном состоянии;

p ₂, V ₂, T ₂ – давление, объем и температура газа в конечном состоянии.

Закон Дальтона, определяющий давление смеси газов,

p = p ₁ + p ₂ +...+ p_n,

где p_i – парциальные давления компонентов смеси;

n – число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молярная масса смеси газов

μ = ,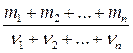

где m_i – масса i -го компонента смеси;

ν _i – количество вещества i -го компонента смеси, ν _i = m_i /μ;

n – число компонентов смеси.

Массовая доля i -го компонента смеси газа (в долях единицы или процентах)

ω_i = m_i / m,

где m – масса смеси.

Концентрация молекул

n = = ,

где N – число молекул, содержащихся в данной системе;

ρ – плотность вещества;

V – объем системы.

Последняя формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов

p = 2/3 n ,

где – средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы

= 3/2 kT,

где k – постоянная Больцмана, k = 1,38·10 ^-23 Дж/К.

Средняя полная кинетическая энергия молекулы

= kT,

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры

p = nkT.

Скорости молекул:

– средняя квадратичная

;

– средняя арифметическая

;

– наиболее вероятная

,

где m ₁ – масса одной молекулы.

Относительная скорость молекулы

,

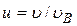где 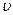– скорость данной молекулы.

Среднее число столкновений молекулы газа за 1 с

,

где d – эффективный диаметр молекулы газа;

n –концентрация молекул газа;

– средняя арифметическая скорость молекул газа.

Средняя длина свободного пробега молекул (расстояние, проходимое молекулой газа между двумя последовательными столкновениями)

.

Удельные теплоемкости газа при постоянном объеме C_v и постоянном давлении C_p:

C _v = 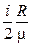; C _p = .

Связь между удельной c и молярной C теплоемкостями

C = C /μ; С = с μ.

Дата добавления: 2014-12-25