
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электростатика. Постоянный электрический ток
|
|
|
|
2.3.1 Основные формулы. Закон Кулона
 F =
F =  ,
,
где F – сила взаимодействия точечных зарядов Q 1 и Q 2;
r – расстояние между зарядами;
ε – диэлектрическая проницаемость среды;
ε 0 – электрическая постоянная.
Напряженность Е и потенциал φ электрического поля
 ;
;  ,
,
где П – потенциальная энергия положительного точечного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда
 ,
,  .
.
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей),
 ;
; 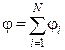 ,
,
где 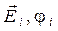 – напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.
– напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом,
 ,
,  ,
,
где r – расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы:
E = 0;  при r < R;
при r < R;
 ;
; 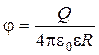 при r = R;
при r = R;
 ;
;  при r > R,
при r > R,
где Q – заряд сферы.
Линейная плотность заряда
τ = Q / l.
Поверхностная плотность заряда
σ = Q /S.
Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью τ, то на линии выделяется малый участок длиной dl с зарядом dQ = τdl. Такой заряд можно рассматривать как точечный и применять формулы
 ;
; 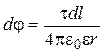 ,
,
где  – радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
– радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность  и потенциал φ поля, создаваемого распределенным зарядом:
и потенциал φ поля, создаваемого распределенным зарядом:
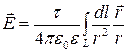 ;
;  .
.
Интегрирование ведется вдоль всей длины L заряженной линии.
Напряженность поля, создаваемого прямой бесконечной равномерно заряженной линией или бесконечно длинным цилиндром,
 ,
,
где r – расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,
 .
.
Связь потенциала с напряженностью:
– в общем случае
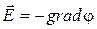 или
или 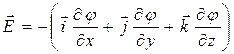 ;
;
– в случае однородного поля
 ;
;
– в случае поля, обладающего центральной или осевой симметрией
 .
.
Электрический момент диполя
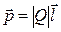 ,
,
где Q – заряд;
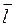 – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Работа сил поля по перемещению заряда Q из точки поля с потенциалом φ1 в точку с потенциалом φ2
A 12 = Q (φ1 – φ2).
Работа сил электростатического поля по перемещению заряда Q по замкнутому контуру L вследствие того, что силы являются консервативными, равна нулю:
 .
.
Циркуляция вектора напряженности электрического поля  по замкнутому контуру L равна нулю:
по замкнутому контуру L равна нулю:
 .
.
Электроемкость
C = Q/ φ или C = Q/U,
где φ – потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю);
U – разность потенциалов пластин конденсатора.
Электроемкость плоского конденсатора
C = ε0εS/d,
где S – площадь пластины (одной) конденсатора;
d – расстояние между пластинами.
Электроемкость батареи конденсаторов:
– при последовательном соединении
 ;
;
– при параллельном соединении
 ,
,
где N – число конденсаторов в батарее.
Энергия заряженного конденсатора
W = QU/ 2; W = CU 2 / 2; W = Q 2 / (2 C).
Сила постоянного тока
I = Q/t,
где Q – заряд, прошедший через поперечное сечение проводника за время t.
Плотность тока
j = I/S,
где S – площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью 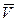 направленного движения заряженных частиц
направленного движения заряженных частиц
j = Qn  ,
,
где Q – заряд частицы;
n – концентрация заряженных частиц.
Закон Ома:
– для участка цепи, не содержащего ЭДС
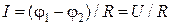 ,
,
где  – разность потенциалов (напряжение) на концах участка цепи,
– разность потенциалов (напряжение) на концах участка цепи,  ;
;
R – электрическое сопротивление участка;
– для участка цепи, содержащего ЭДС
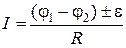 ,
,
где 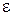 – ЭДС источника тока;
– ЭДС источника тока;
R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
– для замкнутой (полной) цепи
 ,
,
где R – внешнее сопротивление цепи;
r – внутреннее сопротивление цепи.
Законы Кирхгофа:
– первый закон
 ;
;
– второй закон
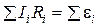 ,
,
где  – алгебраическая сумма токов, сходящихся в узле;
– алгебраическая сумма токов, сходящихся в узле;
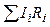 – алгебраическая сумма произведений сил токов на отдельных участках и сопротивления этих участков;
– алгебраическая сумма произведений сил токов на отдельных участках и сопротивления этих участков;
 – алгебраическая сумма ЭДС.
– алгебраическая сумма ЭДС.
Сопротивление R и проводимость G проводника
R = ρl/S; G = γS/l,
где ρ – удельное сопротивление;
γ – удельная проводимость;
l – длина проводника;
S – площадь поперечного сечения проводника.
Зависимость сопротивления проводника от температуры
R = R 0(1 + αt),
где R 0 – сопротивление проводника при нулевой температуре;
α – температурный коэффициент сопротивления;
t – температура.
При последовательном соединении источников ЭДС в батарею складываются как поля их ЭДС
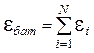 ,
,
так и их внутренние сопротивления
 .
.
Параллельное соединение N источников ЭДС используется, как правило, только для одинаковых источников. В этом случае ЭДС батареи равна ЭДС одного источника ( ), а внутреннее сопротивление батареи
), а внутреннее сопротивление батареи  .
.
Сопротивление системы проводников:
– при последовательном соединении
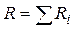 ;
;
– при параллельном соединении
 ,
,
где  – сопротивление i -го проводника.
– сопротивление i -го проводника.
Работа тока
A = IUt; A = I 2Rt; A = U 2t/R.
Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, две последние – для участка, не содержащего ЭДС.
Мощность тока
P = IU; P = I 2R, P = U 2/R.
Закон Джоуля–Ленца
Q = I 2Rt.
Закон Ома в дифференциальной форме
 ,
,
где γ – удельная проводимость;
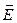 – напряженность электрического поля;
– напряженность электрического поля;
 – плотность тока.
– плотность тока.
Связь удельной проводимости γ с подвижностью b ионов
γ = Qn (b+ + b–),
где Q – заряд иона;
n – концентрация ионов;
b + и b – – подвижности положительных и отрицательных ионов.
2.3.2 Примеры решения задач.
Пример 1 – Три точечных заряда Q 1 = Q 2 = Q 3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q 4 нужно поместить в центре треугольника, чтобы система зарядов находилась в равновесии?
| Дано: | Решение |
| Q 1 = Q 2 = Q 3 = 1 нКл = 10-9 Кл a = b = c = r | Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. |
| Q 4 –? |
Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например Q 1, находился в равновесии. Заряд Q 1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:
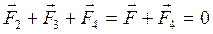 ,
,
где  ,
, 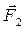 ,
, 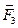 – силы, с которыми соответственно действуют на заряд Q 1 заряды Q 2, Q 3, Q 4;
– силы, с которыми соответственно действуют на заряд Q 1 заряды Q 2, Q 3, Q 4;
 – равнодействующая сил
– равнодействующая сил  и
и  .
.
Так как силы F и F 4 направлены по одной прямой в противоположные стороны, то векторное равенство можно заменить скалярным: F – F 4 = 0, откуда F 4 = F. Выразив в последнем равенстве F через F 2 и F 3 и учитывая, что F 3 = F 2, получим
 .
.
Применив закон Кулона и имея в виду, что Q 2 = Q 3 = Q 1, найдем
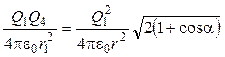 ,
,
откуда
 .
.
Из геометрических построений в равностороннем треугольнике следует, что
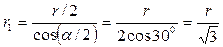 , cos α = cos 600 = 1/2.
, cos α = cos 600 = 1/2.
С учетом этого окончательная формула примет вид:
Q 4 = Q 1/ 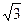 .
.
Произведем вычисления
Q 4 = 10-9/ 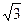 Кл = 5,77∙10-10 Кл.
Кл = 5,77∙10-10 Кл.
Следует отметить, что равновесие системы зарядов будет неустойчивым.
Пример 2. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии a = 10 см от ближайшего конца находится точечный заряд Q 1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность заряда на стержне.
| Дано: l = 20 см = 0,2 м a = 10 см = 0,1 м Q 1 = 40 нКл = 4∙10-8 Кл F = 6 мкН = 6∙10 -6 Н | Решение Сила взаимодействия F заряженного стержня с зарядом Q 1 зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон |
| τ –? |
 Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рисунок 1) малый участок dr с зарядом dQ = τ dr. Этот зарядможно рассматривать как точечный. Тогда, согласно закону Кулона,
Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рисунок 1) малый участок dr с зарядом dQ = τ dr. Этот зарядможно рассматривать как точечный. Тогда, согласно закону Кулона,
 .
.
Интегрируя это выражение в пределах от a до a + l, получаем
 ,
,
откуда
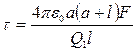 .
.
Выполним проверку размерности:
 =
=

Найденная единица является единицей линейной плотности заряда.
Произведем вычисления:
 Кл/м = 2,5·10–9 Кл/м = 2,5 нКл/м.
Кл/м = 2,5·10–9 Кл/м = 2,5 нКл/м.
Пример 3 – Электрическое поле создано длинным цилиндром радиусом R = 1см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии a 1 = 0,5 см и a 2 = 2 см от поверхности цилиндра в средней его части.
| Дано: | Решение
Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала
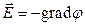 . .
|
| R = 1 см = 10-2 м τ = 20 нКл/м =2∙10-8 Кл/м a 1 = 0,5 см = 0,5∙10-2 м a 2 = 2 см = 2∙10-2 м | |
| φ1 – φ2 –? |
Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде
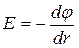 или
или  .
.
Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r1 и r2 от оси цилиндра:
 .
.
Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром:
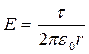 .
.
Подставив в выражение для разности потенциалов, получим
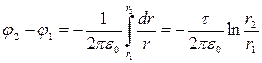
или
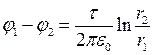 .
.
Произведем вычисления, учитывая, что величины r 1 и r 2, входящие в формулу в виде отношения, можно выразить в сантиметрах (r 1 = R + a 1 = 1,5 см, r 2 = R + a 2= 3 см):
 В.
В.
Пример 4 – Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью V1 = 106м/с, чтобы скорость его возросла в n = 2 раза.
| Дано: | Решение |
| V 1 = 106 м/с n = 2 e = 1,6∙10-19 Кл m e = 9,1∙10-31 кг | Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением элементарного заряда e на разность потенциалов U |
| U –? | A = eU. |
Работа сил электрического поля в данном случае равна изменению кинетической энергии электрона:
 ,
,
где Т 1 и Т 2 – кинетическая энергия электрона до и после прохождения ускоряющего поля;
m e – масса электрона;
V1 и V2 – начальная и конечная скорости электрона.
Приравняв правые части равенств, получим
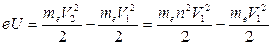 ,
,
где n = V 2/ V 1.
Отсюда искомая разность потенциалов
 .
.
Произведем вычисления:
U = 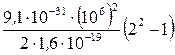 = 8,53 В.
= 8,53 В.
Пример 5 – Конденсатор емкостью C1 = 3 мкФ был заряжен до разности потенциалов U 1 = 40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью C 2= 5 мкФ. Какая энергия W' израсходуется на образование искры в момент присоединения второго конденсатора?
| Дано: | Решение |
| C1 = 3 мкФ = 3∙10-6 Ф U1 = 40 В C2 = 5 мкФ = 5∙10-6 Ф | Энергия, израсходованная на образование искры, W' = W 1– W 2, |
| W' –? | где W 1 – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; |
W2 – энергия, которую имеет батарея, составленная из двух конденсаторов.
Энергия заряженного конденсатора определяется по формуле
W = (1/2) CU 2,
где C – емкость конденсатора или батареи конденсаторов.
Выразив энергии W 1 и W 2 и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим
W = (1/2) C 1 U 12–(1/2)(C 1 + C 2) U 22,
где U 2 – разность потенциалов на зажимах батареи конденсаторов.
Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U 2 следующим образом:
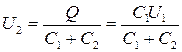 .
.
Подставив выражение U 2 в формулу для W ', найдем
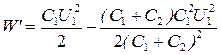 , или
, или  .
.
Произведем вычисления
W' =. 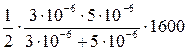 = 1,5 мДж.
= 1,5 мДж.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 589; Нарушение авторских прав?; Мы поможем в написании вашей работы!