
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Первое начало термодинамики. Внутренняя энергия идеального газа
|
|
|
|
Внутренняя энергия идеального газа
Уравнение Майера
C p – Cv = R.
U = 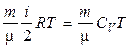 .
.
Q =  U + A,
U + A,
где Q – теплота, сообщенная системе (газу);
 U – изменение внутренней энергии системы;
U – изменение внутренней энергии системы;
A – работа, совершенная системой против внешних сил.
Работа расширения газа:
– в общем случае
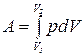 ;
;
– при изобарном процессе
A = p (V 2 – V 1);
– при изотермическом процессе
A = 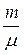 RT ln
RT ln  ;
;
– при адиабатном процессе
 или
или 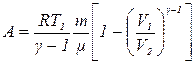 ,
,
где γ – показатель адиабаты, γ = CP / CV.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
pV γ = const,  ;
;
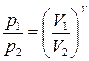
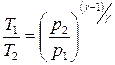 .
.
Коэффициент полезного действия (КПД) цикла
η = 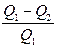 ,
,
где Q 1 – теплота, полученная рабочим телом от нагревателя;
Q 2 – теплота, переданная рабочим телом холодильнику.
КПД цикла Карно
η =  =
=  ,
,
где T 1 и T 2 – термодинамические температуры нагревателя и холодильника.
Разность энтропий двух состояний B и A определяется формулой
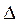 S =
S =  .
.
2.2.2 Примеры решения задач.
Пример 1 – Определить число N молекул, содержащихся в объеме V = 1 мм3 воды, и массу m 1 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.
| Дано: | Решение |
| H2O V = 1 мм3 = 10-9 м3 | Число N молекул, содержащихся в некоторой системе массой m, равно произведению постоянной Авогадро N A и количество вещества ν, = ν N A. Так как ν = m /μ, где μ – молярная масса, то |
| N –? m 1 –? d –? |
N = mN A/μ. Выразив массу как произведение плотности на объем V, получим
N = ρ VN A/μ.
Произведем вычисления, учитывая, что μ = 18·10-3 кг/моль,
N = 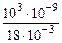 ·6,02·1023 = 3,34·1019 молекул.
·6,02·1023 = 3,34·1019 молекул.
Массу m 1 одной молекулы можно найти по формуле
m 1 = μ/ N A.
Находим массу молекулы воды
m 1 = 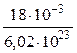 = 2,99·10-26 кг.
= 2,99·10-26 кг.
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) V 1 = d 3, где d –диаметр молекулы. Откуда
d =  .
.
Объем V 1 найдем, разделив молярный объем Vm на число молекул в моле, т. е. на N A V 1 = Vm / N A. Подставив V 1 в формулу для d, получим
d = 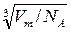 ,
,
где Vm = μ/ρ.
Тогда
d =  .
.
Проверим, дает ли правая часть выражения единицу длины
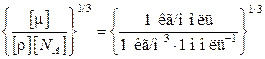 = 1 м.
= 1 м.
Произведем вычисления
d =  = 3,11·10-10 м = 311 пм.
= 3,11·10-10 м = 311 пм.
Пример 2 – Найти среднюю кинетическую энергию  вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию Е к вращательного движения всех молекул кислорода массой m = 4 г.
вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию Е к вращательного движения всех молекул кислорода массой m = 4 г.
| Дано: | Решение |
| О2 μ = 32·10-3 кг/моль Т = 350 К m = 4·10-3 кг | На каждую степень свободы молекулы газа приходится одинаковая средняя энергия
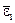 =1/2 kT, =1/2 kT,
|
 –? Е к–? –? Е к–?
| где k – постоянная Больцмана; Т – термодинамическая температура газа. |
Так как вращательному движению двухатомной молекулы (молекула кислорода двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода
 = 2·
= 2·  kT.
kT.
Кинетическая энергия вращательного движения всех молекул газа
Е к =  N.
N.
Число всех молекул газа
N = N A ν,
где N A – постоянная Авогадро;
ν – количество вещества.
Так как количество вещества ν = m /μ, то формула для Е к примет вид:
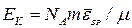 .
.
Произведем вычисления:
 = kT = 1,38·10 -23·350 = 4,83·10-21 Дж;
= kT = 1,38·10 -23·350 = 4,83·10-21 Дж;
Е к = 6,02·1023·  · 4,83·10 -21 = 364 Дж.
· 4,83·10 -21 = 364 Дж.
Пример 3 – Кислород массой m = 2 кг занимает объем V 1 = 1 м3 и находится под давлением p 1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V 2 = 3 м3, а затем при постоянном объеме до давления p 3 = 0,5 МПа. Найти изменение 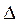 U внутренней энергии газа, совершенную им работу A и теплоту Q, переданную газу.
U внутренней энергии газа, совершенную им работу A и теплоту Q, переданную газу.
| Дано: | Решение |
| μ = 32·10-3 кг/моль m = 2 кг p 1 = 0,2·106 Па V 1 = 1 м3 V 2 = 3 м3 p 3 = 0,5·106 Па | Изменение внутренней энергии газа
U = CVm  T = T = 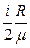 m m  T,
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5); T,
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5);
|
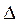 U –? A –? Q –? U –? A –? Q –?
|  T – разность температур газа в конечном (третьем) и начальном состояниях, T – разность температур газа в конечном (третьем) и начальном состояниях,  T = T 3 – T 1. T = T 3 – T 1.
|
Начальную и конечную температуру газа найдем из уравнения Менделеева–Клапейрона pV =  RT, откуда
RT, откуда
T = pV μ/(mR).
Работа расширения газа при постоянном давлении выражается формулой
A 1 = 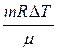 .
.
Работа газа, нагреваемого при постоянном объеме, равна нулю:
A 2 = 0.
Следовательно, полная работа, совершаемая газом,
A = A 1 + A 2 = A 1.
Согласно первому началу термодинамики, теплота, переданная газу, равна сумме изменения внутренней энергии 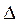 U и работы A:
U и работы A:
Q =  U + A.
U + A.
Произведем вычисления:
T 1 = 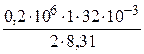 = 385 K;
= 385 K;
T 2 = 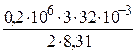 = 1155 K;
= 1155 K;
T 3 =  = 2887 K;
= 2887 K;
A 1 = 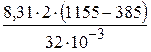 = 0,4·106 = 0,4 МДж; A = A 1 = 0,4 МДж;
= 0,4·106 = 0,4 МДж; A = A 1 = 0,4 МДж;
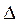 U =
U =  = 3,24·106 = 3,24 МДж;
= 3,24·106 = 3,24 МДж;
Q = 3,24 + 0,4 = 3,64 МДж.
Пример 4 – Тепловая машина работает по обратимому циклу Карно. Температура нагревателя T 1 = 500 K. Определить КПД (η) цикла и температуру T2 холодильника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от нагревателя, машина совершает работу A = 350 Дж.
| Дано: | Решение |
| T 1 = 500 K Q 1 = 103Дж A = 350 Дж | КПД тепловой машины показывает, какая доля теплоты, полученной от нагревателя, превращается в механическую работу. КПД выражается формулой |
| η –? T 2 –? | η = A / Q 1, |
где Q 1 – теплота, полученная от нагревателя;
A – работа, совершенная рабочим телом тепловой машины.
Зная КПД цикла, можно по формуле η = (T 1– T 2)/ T 1 определить температуру холодильника T 2
T 2 = T 1(1 – η).
Произведем вычисления:
η = 350 / 10 3 = 0,35; T 2 = 500 (1 – 0,35) = 325 K.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 341; Нарушение авторских прав?; Мы поможем в написании вашей работы!