Магнетизм

2.4.1 Основные формулы. Связь магнитной индукции 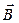с напряженностью 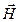магнитного поля

,

где μ – магнитная проницаемость изотропной среды;

μ ₀ – магнитная постоянная, μ ₀ = 4π∙10^-7 Гн/м.

В вакууме μ = 1, и тогда магнитная индукция в вакууме

.

Закон Био–Савара–Лапласа

или ,

где 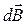– магнитная индукция поля, создаваемого элементом проводника длиной d l с током I;

– радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;

α – угол между радиусом-вектором и направлением тока в элементе провода.

Магнитная индукция в центре кругового витка с током

,

где R – радиус кругового витка.

Магнитная индукция на оси кругового витка с током

,

где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямолинейного проводника с током

B = μμ₀ I /(2π r ₀),

где r ₀ – расстояние от оси проводника до точки, в которой определяется магнитная индукция.

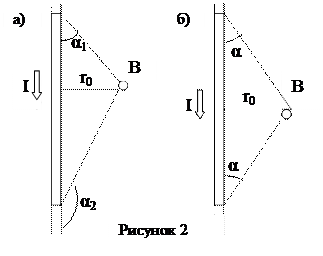Магнитная индукция поля, создаваемого отрезком проводника с током (рисунок 2, а),

.

Обозначения ясны из рисунка 2. Направление вектора магнитной индукции обозначено точкой – это значит, что 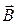направлен перпендикулярно плоскости чертежа к нам. При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рисунок 2, б), –cosα₂ = cosα₁ = cosα, тогда

.

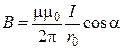Магнитная индукция поля внутри соленоида

B = μμ ₀ nI,

где n – отношение числа витков соленоида к его длине.

Сила, действующая на проводник с током в магнитном поле (закон Ампера),

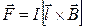, или ,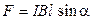

где l – длина проводника;

α – угол между направлением тока в проводнике и вектором магнитной индукции .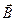

Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера применяют к каждому элементу d l проводника в отдельности:

.

Магнитный момент плоского контура с током

,

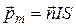где – единичный вектор нормали (положительной) к плоскости контура;

I – сила тока, протекающего по контуру;

S – площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,

или ,

где α – угол между векторами и .

Потенциальная энергия (механическая) контура с током в магнитном поле

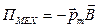или .

Отношение магнитного момента p_m к механическому моменту L (моменту импульса) заряженной частицы, движущейся по круговой орбите,

,

где Q – заряд частицы;

m – масса частицы.

Сила Лоренца

или ,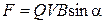

где 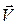– скорость заряженной частицы;

α – угол между векторам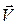и и .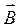

Магнитный поток:

– в случае однородного магнитного поля и плоской поверхности

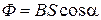или ,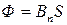

где S – площадь контура;

α – угол между нормалью к плоскости контура и вектором магнитной индукции.

– в случае неоднородного поля и произвольной поверхности

(интегрирование ведется по всей поверхности).

Потокосцепление (полный поток)

.

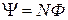Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Работа по перемещению замкнутого контура в магнитном поле

.

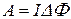ЭДС индукции

.

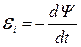Разность потенциалов на концах проводника, движущегося со скоростью 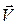в магнитном поле,

,

где l – длина проводника;

α – угол между векторам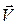и и .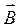

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур,

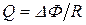или ,

где R – электрическое сопротивление контура.

Индуктивность контура

.

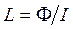ЭДС самоиндукции

.

Индуктивность соленоида

,

где n – отношение числа витков соленоида к его длине;

V – объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

– при замыкании цепи

,

где 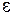– ЭДС источника тока;

t – время, прошедшее после замыкания цепи;

– при размыкании цепи

,

где I ₀ – сила тока в цепи при t = 0;

t – время, прошедшее с момента размыкания цепи.

Энергия магнитного поля проводника с током

.

Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)

, или , или ,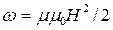

где B – магнитная индукция;

H – напряженность магнитного поля.

2.4.2 Примеры решения задач.

Пример 1 – По двум параллельным прямым проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.

Дано:	Решение
L = 2,5 м d = 20 см = 0,2 м I = 1 кА = 10^3 А	Взаимодействие двух проводов, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой провод.
F –?

Предположим, что оба тока (обозначим их для удобства I₁ и I₂) текут в одном направлении. Ток I ₁ создает в месте расположения второго провода (с током I ₂) магнитное поле.

Проведем линию магнитной индукции (пунктир на рисунке 3) через второй провод и по касательной к ней – вектор магнитной индукции . Модуль магнитной индукции B ₁ определяется соотношением

.

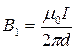Согласно закону Ампера, на каждый элемент второго провода с током I₂ длиной dl действует в магнитном поле сила

.

Так как вектор перпендикулярен вектору , то и тогда

dF = I ₂ B ₁ dl.

Подставив в это выражение B ₁, получим

.

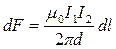Силу взаимодействия проводов с током найдем интегрированием:

.

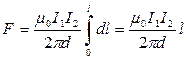Заметив, что I ₁ = I ₂ = I, получим

.

Анализ размерности:

= .

Произведем вычисления

F = .

Направление действия сил F и dF совпадает и определяется правилом левой руки.

Пример 2 – Короткая катушка, содержащая N = 10³ витков, равномерно вращается с частотой n = 10 с^-1 относительно оси АВ, лежащей в плоскости катушки и перпендикулярной линиям однородного магнитного поля (B = 0,04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость катушки составляет угол α = 60⁰ с линиями поля. Площадь S катушки равна 100 см².

Дано:	Решение
N = 10^3 n = 10 с^-1 B = 0,04 Тл α = 60^0 S = 100 см^2= 10^-2 м^2	Мгновенное значение ЭДС индукции ε определяется основным уравнением электромагнитной индукции Фарадея–Максвелла: ,
ε –?	где ψ – потокосцепление, ψ = N Ф;

N – число витков катушки, пронизываемых магнитным потоком Ф.

Подставив выражение ψ в формулу, получим

.

При вращении катушки магнитный поток Ф, пронизывающий катушку в момент времени t, изменяется по закону

Ф = BS cosω t,

где B – магнитная индукция;

S – площадь катушки;

ω – угловая скорость катушки.

Подставив в формулу для ε выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:

.

Заметив, что угловая скорость ω связана с частотой вращения n катушки соотношением ω = 2π n и что угол ωt = π/2 – α, получим

.

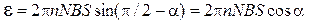Анализ размерности:

=

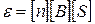Произведем вычисления:

ε = 2∙3,14∙10∙10³∙0,04∙10^-2∙0,5 = 25,1 В.

Дата добавления: 2014-12-25