Учебник по навигации

(возможно, под редакцией капитана дальнего плавания
Врунгеля Христофора Бонифатьевича)

"Навигацию у нас в мореходном училище преподавал Христофор Бонифатьевич Врунгель.
- Навигация, - сказал он на первом уроке, - это наука, которая учит нас избирать наиболее безопасные и выгодные морские пути, прокладывать эти пути на картах и водить по ним корабли... Навигация, - добавил он напоследок, - наука не точная. Для того чтобы вполне овладеть ею, необходим личный опыт продолжительного практического плавания..."
Из книги Александра Носова "Приключения капитана Врунгеля"

Времени на учебник уйдет, конечно, уйма, не один день. (Сканировать будем из учебника "Навигация"). Но, думаем, он будет полезен для тех, кто учится (очно или заочно) в мореходках.
В данном учебнике будут следующие главы:

Глава 1
Земной эллипсоид

§ 1 Фигура и размеры Земли
§ 2 Географическая система координат
§ 3 Разность широт и разность долгот
§ 4 Понятие о радиусах кривизны главных сечений в данной точке земного эллипсоида
§ 5 Длина одной минуты дуги меридиана земного эллипсоида. Меры длины и скорости, принятые в кораблевождении.
§ 6 Видимый горизонт и его дальность
§ 7 Дальность видимости ориентиров на море

Глава 2
Ориентирование корабля в море

§ 8 Система счета направлений в плоскости истинного горизонта
§ 9 Истинный курс, истинный пеленг и курсовой угол
§ 10 Понятие о корабельных указателях направлений
§ 11 Понятие о магнитном поле Земли
§ 12 Магнитные направления
§ 13 Понятие о магнитном поле корабля. Девиация магнитного компаса
§ 14 Компасные направления
§ 15 Поправка компаса и способы ее определения
§ 16 Расчет компасных, магнитных и истинных направлений

Глава 3
Определение скорости хода, пройденного кораблем расстояния и поправки лага

§ 17 Определение пройденного кораблем расстояния по скорости хода и продолжительности плавания
§ 18 Определение пройденного кораблем расстояния по показаниям лага

Глава 4
Основные сведения из теории картографических проекций

§ 19 Понятие о картографической проекции. Карта. План
§ 20 Нормальная, поперечная и косая картографические сетки
§ 21 Масштаб карты. Характеристика искажений проекции
§ 22 Некоторые сведения из теории искажений
§ 23 Классификация картографических проекций
§ 24 Понятие об изображении земного эллипсоида на шаре

Глава 5
Цилиндрические проекции, применяемые для построения морских навигационных карт

§ 25 Основные требования, предъявляемые к морской навигационной карте
§ 26 Общие формулы цилиндрических проекций
§ 27 Равноугольная цилиндрическая проекция Меркатора
§ 28 Локсодромия
§ 29 Изменение масштаба на карте и проекции Меркатора
§ 30 Понятие о построении картографической сетки проекции Мерактора
§ 31 Поперечная цилиндрическая равноугольная проекция Гаусса
§ 32 Сферические прямоугольные координаты
§ 36 Применение карт в проекции Гаусса для навигационных целей
§ 37 Топографические карты, их номенклатура и использование в кораблевождении

Глава 9
Графический способ счисления пути корабля

§ 46 Основные понятия и определения
§ 47 Элементарные задачи навигационной прокладки, решаемые на карте в проекции Меркатора
§ 48 Графический способ счисления по показаниям компаса, лага и часов
§ 49 Циркуляция корабля. Способы учета циркуляции в прокладке
§ 50 Влияние ветра на движение корабля. Определение угла ветрового дрейфа
§ 51 Предвычисление дрейфа и изменения скорости хода корабля под влиянием ветра и волнения
§ 52 Учет дрейфа корабля при счислении
§ 53 Влияние течения на путь корабля. Основы учета течения при графическом способе счисления пути корабля
§ 54 Совместный учет дрейфа и течения
§ 55 Основные способы получения сведений об элементах течения. Разгон невязки счисления

Глава 12
Определение места по видимым с корабля ориентирам

§ 75 Организация работы штурмана при определении места корабля
§ 76 Определение места корабля по двум горизонтальным углам
§ 77 Определение места корабля по пеленгам на три ориентира
§ 78 Определение места корабля по пеленгам на два ориентира
§ 79 Определение места корабля по расстояниям до двух и трех ориентиров
§ 80 Определение расстояния до ориентира по вертикальному углу
§ 81 Определение места корабля по двум разновременно измеренным пеленгам (крюйс-пеленг)
§ 82 Определение места корабля по разновременно измеренным расстояниям
§ 83 Определение места по пеленгу и расстоянию до ориентира

Глава 1

С развитием мореплавания в тесной взаимосвязи и диалектическом единстве с ним развивается и кораблевождение, достигшее к настоящему времени высокого совершенства.
Термин кораблевождение принято употреблять для выражения двух понятий. В узком значении этот термин употребляют для обозначения непосредственного процесса вождения корабля, включающего штурманские расчеты, графическое изображение пути на карте, контроль за положением и движением корабля и управление кораблем с помощью рулевого устройства. В более широком и общем значении термин кораблевождение принято понимать как науку, которая изучает условия, средства и способы вождения кораблей и включает в себя дисциплины: Навигацию, Мореходную астрономию, Маневрирование, Технические средства кораблевождения, Навигационные пособия и Морскую гидрометеорологию.
Поясним это. Корабль, совершающий плавание, движется не только под действием своих движителей — гребных винтов, паруса или реактивной силы. Находясь одновременно в двух средах — воздушной и водной, корабль подвергается воздействию этих сред и процессов, происходящих в них (ветер, течение, волнение и др.). В результате влияния всех сил, действующих на корпус и надстройки корабля, корабль движется в направлении их, равнодействующей. Если не будет учтена хотя бы одна из этих сил, корабль уклонится от намеченного маршрута, возникнут предпосылки, которые в сочетании с другими неблагоприятными обстоятельствами (малая видимость, отсутствие возможностей для контроля места корабля, опасный в навигационном отношении район плавания и т.п.) могут привести к аварии. Учесть многообразные факторы, влияющие на направление и скорость движения корабля, и успешно решить общую задачу кораблевождения — точно, безопасно, в установленное время провести корабль по заданному маршруту — штурман может только тогда, когда он вооружен знаниями условий плавания, маневренных свойств корабля, средств и способов вождения кораблей.
Знания условий плавания — атмосферы, Мирового океана и процессов, происходящих в них,— могут быть получены в результате изучения Морской гидрометеорология данного морского театра.
Маневренные свойства корабля и влияние на них различных факторов — мелководья, обрастания корпуса, крена, дифферента, изменения водоизмещения и др.— изучаются в Теории корабля. Основные маневренные элементы корабля (скорость хода, дальность плавания, инерция, циркуляция и т. д.),-характеризующие его маневренные свойства, определяются и периодически проверяются штурманом на специально оборудованных для этой цели полигонах.
Техническое оснащение (навигационные приборы, системы и комплексы), с помощью которого штурман осуществляет вождение корабля, изучается в Технических средствах кораблевождения.
Способы определения места корабля, поправок корабельных указателей направлений по наблюдениям небесных светил и способы решения некоторых других задач кораблевождения и военно-морской практики изучаются Мореходной астрономией. Однако ведущей дисциплиной науки Кораблевождение является Навигация.
Навигация — дисциплина, изучающая и разрабатывающая теорию и.практические способы вождения кораблей. Из этого определения видно, что именно навигация призвана непосредственно решать общую задачу кораблевождения. Для этого навигация реализует достижения и результаты всех дисциплин, составляющих кораблевождение, а также некоторых дисциплин и наук, не вошедших в него.
Слово «навигация» происходит от латинского слова navigatio, означающего судоходство, мореплавание.

ЗЕМНОЙ ЭЛЛИПСОИД

§ 1. Фигура и размеры Земли

Многочисленные исследования и измерения позволили установить, что Земля имеет форму неправильного в математическом отношении тела, называемого геоидом. Поверхность, образующая геоид, в отличие от физической поверхности Земли с ее неровностями (горы, впадины и т. п.) во всех своих точках горизонтальна, т. е. совпадает с нормалью к направлению силы тяжести и определяется как уровенная поверхность. В природе такая уровенная поверхность совпадает со средним уровнем воды океанов и открытых морей в спокойном состоянии (при отсутствии,волнения, течений, приливов и других возмущающих факторов), мысленно продолженным под все материки. Неправильность геоида обусловливается неравномерным распределением масс в толще Земли, от притягивающего действия которых зависит направление силы тяжести.
Теоретические исследования и результаты обработки астрономо-геодезических и гравиметрических измерений, а также результаты наблюдений за искусственными спутниками Земли показывают, что геоид близок к математически правильной фигуре — эллипсоиду вращения, образованному вращением эллипса вокруг его малой оси. Поэтому при производстве геодезических, картографических и других работ, требующих высокой точности, за фигуру Земли принимают эллипсоид вращения.
Величина отклонения по высоте поверхности геоида от поверхности земного эллипсоида, принятого в СССР и надлежащим образом подобранного по размерам и ориентированного в теле Земли, не превышает 100—150 м. Эллипсоид вращения практически отождествляется со сфероидом, представляющим фигуру равновесия вращающейся однородной жидкой массы. Отклонение по высоте поверхностей эллипсоида вращения и сфероида не превышает 2—3 м.

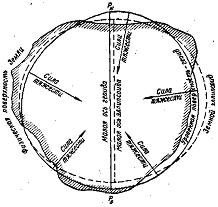
Определение размеров земного эллипсоида, имеющего наибольшую близость к фигуре Земли в целом, продолжает оставаться одной из основных задач высшей геодезии. Поэтому в разных странах обработку результатов геодезических и топографических работ относят к вспомогательной математической поверхности, представляющей земной эллипсоид с размерами, принятыми для данной страны. Эллипсоид с определенными размерами, к поверхности которого относят все результаты геодезических и топографических работ в государстве, называют референц - эллипсоидом.
Основными элементами, определяющими размеры земного эллипсоида, являются его полуоси: большая а и малая Ь. Кроме того, для характеристики земного эллипсоида, а также для некоторых расчетов применяются понятия: полярное сжатие α земного эллипсоида, выражаемое формулой
α = а - b / a, (1 формула)
и эксцентрицитет его (е), определяемый выражением
e = √ a² - b² / a (2 формула)
Начиная с 1946 г. для всех геодезических и картографических работ на территории СССР принимается референц-эллипсоид Ф. Н. Красовского с размерами:
— большая полуось а = 6 378 245 м;
— малая полуось b = 6 356 863 м;
— полярное сжатие α = 1:298,3;
— квадрат эксцентрицитета е²=1:149,15.

При выводе размеров референц-эллипсоида группой ученых, геодезистов, топографов и вычислителей под руководством профессора Ф. Н. Красовского были использованы обширнейшие материалы астрономических, геодезических и гравиметрических измерений, производившихся в СССР на протяжении многих лет, а также результаты аналогичных работ, выполненных в других странах. Размеры референц-эллипсоида Красовского подтверждаются также результатами обработки наблюдений за искусственными спутниками Земли, произведенных в последние годы.
Ориентирование в теле Земли земного эллипсоида с соответствующими размерами полуосей и сжатия характеризуется так называемыми исходными геодезическими датами. Исходными геодезическими датами называют координаты начального пункта триангуляции, определяющие его Широту В₀, долготу L₀, азимут A₀ на какой-либо смежный пункт и высоту h₀ поверхности геоида относительно поверхности референц-эллипсоида.
Эти даты принимаются за начальные при расчете координат всех других пунктов земной поверхности.
При- пользовании иностранными. картами следует помнить, что в разных странах приняты различные исходные геодезические даты. Поэтому одни и те же пункты на картах, изданных в разных странах, могут иметь различные координаты. Хотя это различие может быть и небольшим, но с ним в кораблевождении нужно считаться и перенос места корабля с одной карты на другую при плавании вблизи берегов следует производить не по географическим координатам, а по направлению и расстоянию до ближайшего опорного пункта, помещенного на обеих картах.
Принятие Земли за эллипсоид вращения является, по существу, вторым приближением при определении фигуры Земли. При решении некоторых задач практической навигации, не требующих высокой точности, оказывается возможным ограничиваться первым приближением в определении формы Земли — принимать Землю за шар. К таким задачам относятся вычисления дальности видимости ориентиров в море, расчеты для плавания по кратчайшему расстоянию, аналитические расчеты при определении места по радиопеленгам, расчеты по формулам аналитического счисления и некоторые другие.
Для определения величины радиуса Земли — шара обычно исходят из некоторых дополнительных условий.
Одним из них является условие, чтобы длина одной минуты дуги меридиана (или любого большого круга на шаре) была равна 1852 м, т. е. длине стандартной морской мили. В этом случае радиус шара, отвечающего поставленному условию, получится равным
R = 1852 * 60 * 360 / 2 π = 6 366 707 м.
При решении ряда задач картографии ставится условие, чтобы объем земного шара был равен объему земного эллипсоида или чтобы поверхность шара была равна поверхности эллипсоида. Длина радиуса R шара, одинакового с земным эллипсоидом объема, равна
R = кубический корень √ (a² * b) = 6371109,7 м.
Если ставится условие, чтобы поверхность шара была равна поверхности эллипсоида, то радиус такого шара принимается равным

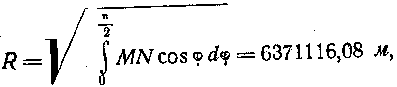
где М— радиус кривизны меридиана; N — радиус кривизны первого вертикала в данной точке.

§ 2. Географическая система координат

Положение точки на любой поверхности или в пространстве определяется совокупностью конкретных величин, называемых координатами. Координаты могут выражаться как в линейной, так и в угловой мере; они определяют положение координатных линий относительно принятых за начало осей координат. Для определения положения точек на земной поверхности могут применяться различные системы координат: географическая, прямоугольная, полярная и др. Наиболее употребительной является система географических координат.
Малая ось эллипсоида пересекает поверхность последнего в двух точках, которые называются северными и южным полюсами. Плоскости, проходящие через ось вращения Земли, называются плоскостями земных меридианов, которые в сечении с поверхностью Земли образуют большие круги, называемые меридианами. Плоскость, перпендикулярная земной оси и проходящая через центр эллипсоида, называется плоскостью экватора. Большой круг, образующийся от пересечения этой плоскости с поверхностью эллипсоида, называется земным экватором. Плоскости, параллельные плоскости земного экватора в сечении с поверхностью Земли, образуют малые круги, называемые земными параллелями.

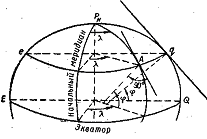
Координатными осями системы географических координат приняты: экватор и один из меридианов, принимаемый за начальный; координатными линиями являются земные параллели и меридианы, а величинами, определяющими положение точек, т. е. координатами, географическая широта и географическая долгота.
Географической широтой точки на поверхности Земли называется угол между нормалью к поверхности эллипсоида в этой точке и плоскостью экватора. Географическая широта в кораблевождении обозначается греческой буквой φ (фи). Счет широт ведется от экватора к полюсам от 0 до 90°. Широты северного полушария считаются положительными и при аналитических расчетах они принимаются со знаком плюс. Северные широты обозначаются буквой N. Широты точек южного полушария, обозначаемые буквой S, считаются отрицательными и им приписывается знак минус.
Географическая широта определяет положение параллели, на которой находится определяемая точка.
Географической долготой точки называется двугранный угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через эту точку. Двугранный угол измеряется сферическим углом при полюсе между начальным меридианом и меридианом определяемой точки или численно равной ему дугой экватора, заключенной между названными меридианами.
За начальный меридиан в принципе может приниматься любой земной меридиан. По международному соглашению 1884 г. большинством стран мира, в том числе и Советским Союзом, за начальный принят меридиан, проходящий через Гринвичскую обсерваторию, расположенную около Лондона.
Счет географических долгот ведется к востоку и западу от Гринвичского меридиана от 0 до 180°. Географическая долгота в кораблевождении обозначается греческой буквой λ (ламбда). Долготы точек, находящихся в восточном полушарии, принято считать положительными (знак плюс), западные долготы считаются отрицательными (знак минус). При определении долготы той или иной точки земной поверхности обязательно указывают на ее наименование: восточной — Оst или, как сейчас принято, Е, западной — W. В зависимости от метода вычисления- географических координат различают координаты геодезические и астрономические.
В геометрическом определении геодезических координат, которые получаются в результате геодезических измерений (триангуляции, полигонометрии), никакой разницы с общей формулировкой географических координат нет. Места точек, фиксируемых геодезической широтой и геодезической долготой, относятся также к математически правильной фигуре—эллипсоиду вращения.
При определении места астрономическими способами наблюдатель имеет дело с линией отвеса, совпадающей с направлением силы тяжести, а не с нормалью к поверхности эллипсоида. Поэтому в астрономической системе координат широта определится как угол между плоскостью экватора и направлением отвеса в данной точке. Долгота места, определенного астрономическим способом, представляет собой двугранный угол между плоскостью начального меридиана (меридиана Гринвича) и плоскостью астрономического меридиана данной точки. Примененный термин—астрономический меридиан — надо понимать как след от сечения земной поверхности плоскостью, проходящей через отвесную линию в данной точке и параллельной оси мира. Из определения астрономических координат видно, что они в отличие от геодезических координат фиксируют положение точек относительно поверхности действительной фигуры Земли—геоида.

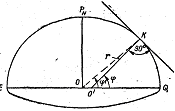
Нормаль к поверхности земного эллипсоида в общем случае не проходит через центр Земли. Вместе с тем при решении астрономических задач, а также ряда специальных задач математической картографии появляется необходимость определять положение точек земной поверхности относительно центра Земли. В этом случае долгота произвольной точки К определится также, как и в географической системе координат, а, широта получится как угол между плоскостью экватора и прямой, соединяющей данную точку с центром эллипсоида. Такая широта называется геоцентрической широтой и обозначается φ'. На рисунке видно, что геоцентрическая широта в общем случае меньше географической широты на величину редукции r широты, которая может быть подсчитана по формуле
r'' = φ - φ' = α sin 2 φ / arc 1'' (3 формула)
Для точек, расположенных на экваторе и на полюсе, редукция широты равна нулю. Наибольшего значения (11,5') редукция достигает в широте 45°.
В случаях, когда форма Земли принимается за шар, положение точек на Земле—шаре определяется так же, как и на поверхности эллипсоида, их географическими координатами, т. е. широтой и долготой. Но нормаль на Земле—шаре совпадает с его радиусом.
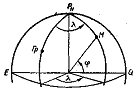Поэтому географической широтой φ некоторой точки М на земном шаре будет угол при центре сферы между плоскостью экватора и радиусом, проходящим через определяемую точку. Из сопоставления определений широты видно, что геоцентрическая широта является лишь частным случаем широты сферической.

§ 3. Разность широт и разность долгот

Географические координаты — широта и долгота — однозначно определяют положение конкретной точки земной поверхности. Переход от одной точки земной поверхности к другой сопровождается изменением их географических координат. Точки, лежащие на одной параллели, имеют одинаковую широту и разные долготы. Точки, расположенные на одном меридиане, имеют одну и ту же долготу и различные широты. В общем случае две точки, не находящиеся на одном меридиане или на одной параллели, имеют разные широты и разные долготы. В практике кораблевождения часто необходимо знать, как изменились или изменятся географические координаты при переходе из одной точки земной поверхности в другую, и уметь вычислять эти изменения. Величинами, характеризующими изменение географических координат при переходе от одной точки земной поверхности к другой, являются разность широт и разность долгот.
Разностью широт (РШ) двух точек на поверхности Земли называется дуга меридиана, заключенная между параллелями этих точек.
Для вычисления разности широт пользуются формулой
РШ = φ₂ - φ₁,
принимая во внимание при этом знаки + и - соответственно их наименованию. Действительно, на рисунке видно, что изменение широты (РШ) при переходе корабля из точки А в точку Б характеризуется дугой А'Б, численно равной разности дуг меридианов точек прихода Б и отхода А, определяемых соответственно широтами φ_Б и φ_А.
Рассчитанной по формуле (4) разности широт приписывается знак плюс, если она совершена к N, и знак минус, если разность широт совершена к S. Разность широт может изменяться от 0 до ±180°.
Разность долгот (РД), характеризующая изменение долготы, как видно из рисунка, представляет собой центральный угол между меридианами двух точек. Этот угол измеряется дугой экватора между указанными меридианами. На этом основании разностью долгот двух точек на поверхности Земли называется меньшая из дуг экватора, заключенная между меридианами этих точек. Из этого определения следует, что разность долгот может иметь значения от 0 до ±180°. С учетом ранее принятых обозначений (для восточной долготы знак плюс и для западной — минус) можно написать формулу для вычисления РД двух точек:
РД = λ₂ - λ₁
Разность долгот будет иметь знак плюс, если она совершена к Ost, и знак минус, если она совершена к W. Указанное правило имеет следующий геометрический смысл: если меридиан пункта прихода λ 2 располагается восточнее меридиана пункта отхода λ 1, значит, разность долгот сделана к Оst и ей приписывается знак плюс. И наоборот, когда меридиан пункта прихода расположен западнее меридиана пункта отхода, разность долгот сделана к W и ей приписывается знак минус.

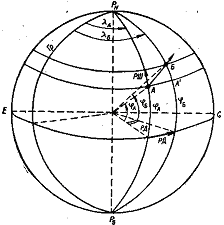
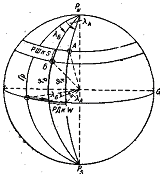
При решении задачи на расчет РД по формуле может получиться результат, превышающий 180°. В этих случаях для нахождения меньшей из дуг экватора полученный результат следует вычесть из 360° и изменить знак (наименование) его на обратный.

Дата добавления: 2014-12-25