Дальность видимого горизонта

Высота е в метрах	Расст. в милях	Высота е в метрах	Расст. в милях	Высота е в метрах	Расст. в милях	Высота е в метрах	Расст. в милях	Высота е в метрах	Расст. в милях	Высота е в метрах	Расст. в милях
0,25	1,0	8,0	5,9		10,6		15,0		21,8		62,4
0,50	1,5	8,5	6,1		10,8		15,3		22,8		65,8
0,75	1,8	9,0	6.2		11.0		15.6		23.7		69.0
1.00	2.1	9.5	6.4		11.2		15.8		24.6		72.1
1.25	2.3	10.0	6.6		11.4		16.1		25.5		75.0
1.50	2.6	10.5	6.7		11.6		16.4		26.3		77.8
1.75	2.8	11.0	6.9		11.8		16.6		27.1		80.6
2.00	2.9	11.5	7.1		12.0		16.9		27.9		83.2
2.25	3.1	12.0	7.2		12.1		17.1		28.7		85.8
2.50	3.3	12.5	7.4		12.3		17.4		29.4		88.3
2.75	3.4	13.0	7.5		12.5		17.7		30.2		90.8
3.00	3.6	13.5	7.6		12.7		17.9		30.9		93.0
3.25	3.8	14.0	7.8		12.8		18.1		31.6		95.3
3.50	3.9	14.5	7.9		13.0		18.4		32.2		97.6
3.75	4.0	15.0	8.1		13.2		18.6		32.9		99.8
4.00	4.2	16.0	8.3		13.3		18.8		33.5		101.9
4.25	4.3	17.0	8.6		13.5		19.1		34.2		108.0
4.50	4.4	18.0	8.8		13.6		19.3		34.8		113.9
4.75	4.5	19.0	9.1		13.8		19.5		35.4		119.5
5.0	4.7	20.0	9.3		14.0		19.7		36.0		124.8
5.5	4.9	21.0	9.5		14.1		20.0		41.6		129.9
6.0	5.1	22.0	9.8		14.3		20.2		46.5		134.8
6.5	5.3	23.0	10.0		14.4		20.4		51.0		139.5
7.0	5.5	24.0	10.2		14.6		20.6		55.0		144.1
7.5	5.7	25.0	10.4		14.7		20.8		58.9		148.5

§ 7. Дальность видимости ориентиров на море

Наблюдатель, находясь в море, может увидеть тот или иной ориентир лишь в том случае, если его глаз окажется выше траектории или, в предельном случае, на самой траектории луча, идущего от вершины ориентира касательно к поверхности Земли (смотрите рисунок). Очевидно, что упомянутый предельный случай будет соответствовать моменту, когда ориентир открывается приближающемуся к нему наблюдателю или скрывается, когда наблюдатель удаляется от ориентира. Расстояние по поверхности Земли между наблюдателем (точка С), глаз которого находится в точке С1 и объектом наблюдения В с вершиной в точке В1 соответствующее моменту открытия или скрытия этого объекта, называется дальностью видимости ориентира.

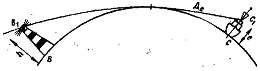
На рисунке видно, что дальность видимости ориентира В складывается из дальности видимого горизонта ВА с высоты ориентира h и дальности видимого горизонта АС с высоты глаза наблюдателя е, т. е.
Д_п = дуга ВС = дуга ВА + дуга АС
или
Д_п = 2,08√ h + 2,08√ e = 2,08 (√ h + √ e) (18)
Дальность видимости, рассчитанная по формуле (18), называется географической дальностью видимости предмета. Ее можно рассчитать, сложив выбранные из упомянутой выше табл. 22-а МТ раздельно дальности видимого горизонта для каждой из заданных высот h u e

Пример 1.

Требуется рассчитать полную дальность видимости предмета, имеющего высоту h=144 м, с высоты глаза наблюдателя e = 16 м.

Решение.

По табл. 22-а находим Д_h=25 миль, Д_e =8,3 мили.
Следовательно,
Д_п = 25,0 +8,3 = 33,3 мили.
Табл. 22-в, помещенная в МТ, дает возможность непосредственно получить полную дальность видимости ориентира по его высоте и высоте глаза наблюдателя. Табл. 22-в рассчитана по формуле (18).
Эту таблицу вы можете увидеть здесь.
На морских картах и в навигационных пособиях показывается дальность видимости Д„ ориентиров для постоянной высоты глаза наблюдателя, равной 5 м. Дальность же открытия и скрытия предметов в море для наблюдателя, высота глаза которого не равна- 5 м, не будет соответствовать дальности видимости Дк, показанной на карте. В таких случаях дальность видимости ориентиров, показанную на карте или в пособиях, необходимо исправлять поправкой за разность высоты глаза наблюдателя и высоты, равной 5 м. Эта поправка может быть рассчитана исходя из следующих соображений:
Д_п = Д_h + Д_е,
Д_к = Д_h + Д₅,
Д_h = Д_к - Д₅,
где Д₅ — дальность видимого горизонта для высоты глаза наблюдателя, равной 5 м.
Подставим из последнего равенства значение Д_h в первое:
Д_п = Д_к - Д₅ + Д_е
или
Д_п = Д_к + (Д_е - Д₅) = Д_к + ▲ Д_к (19)

Разность (Д_е — Д₅) = ▲ Д_к и является искомой поправкой к дальности видимости ориентира (огня), указанной на карте, за разность высоты глаза наблюдателя и высоты, равной 5 м.
Таким образом, чтобы рассчитать дальность видимости ориентира при высоте глаза е ≠ 5 м, надо к дальности, показанной на карте или в навигационном пособии, алгебраически прибавить поправку ▲ Д_к.
Для удобства на походе можно рекомендовать штурману иметь на мостике поправки, заранее рассчитанные для различных уровней глаза наблюдателя, находящегося на различных надстройках корабля (палуба, ходовой мостик, сигнальный мостик, места установки пелорусов гирокомпаса и т. п.).

Пример 2. На карте у маяка показана дальность видимости Д_к = 18 миль, Рассчитать дальность видимости Д_п этого маяка с высоты глаза 12 м и высоту маяка h.

Решение.

По табл. 22-а МТ находим Д₅ = 4,7 мили, Д_е = 7,2 мили.
Рассчитываем ▲ Д_к = 7,2 — 4,7=+2,5 мили. Следовательно, дальность видимости маяка с е = 12 м будет равна Д_п = 18+2,5= =20,5 мили.
По формуле Д_к = Д_h + Д₅ определим
Д_h = 18 — 4,7=13,3 мили.
По табл. 22-а МТ обратным входом находим h = 41 м.

Все изложенное о дальности видимости предметов в море относится к дневному времени, когда прозрачность атмосферы соответствует среднему ее состоянию. Во время переходов штурман должен учитывать возможные отклонения состояния атмосферы от средних условий, накапливать опыт оценки условий видимости, с тем чтобы научиться предвидеть возможные изменения в дальности видимости предметов в море.
В ночное время дальность видимости маячных огней определяется оптической дальностью видимости. Оптическая дальность видимости огня зависит от силы источника света, от свойств оптической системы маяка, прозрачности атмосферы и от высоты установки огня. Оптическая дальность видимости может быть больше или меньше дневной видимости одного и того же маяка или огня; эта дальность определяется экспериментальным путем из многократных наблюдений. Оптическая дальность видимости маяков и огней подбирается для ясной погоды. Обычно светооптические системы подбирают так, чтобы оптическая и дневная географическая дальности видимости были одинаковыми. Если эти дальности отличаются одна от другой, то на карте указывается меньшая из них.
Дальность видимости горизонта и дальность видимости предметов для реальной атмосферы можно определить опытным путем с помощью радиолокационной станции или по обсервациям.

Глава 2

Ориентирование корабля в море

§ 8. Система счета направлений в плоскости истинного горизонта

Основными направлениями, относящимися к фигуре Земли и ее поверхности, являются направление отвесной линии (силы тяжести) и направление оси вращения Земли. Всякая плоскость, проходящая через отвесную линию, является вертикальной плоскостью, а плоскости, перпендикулярные направлению силы тяжести, называются горизонтальными плоскостями. Воображаемая горизонтальная плоскость, проходящая через глаз наблюдателя, называется плоскостью истинного горизонта наблюдателя.
Пусть наблюдатель находится на земной поверхности в точке В (смотрите рисунок). Тогда плоскость, перпендикулярная направлению силы тяжести и проходящая через точку А — глаз наблюдателя —будет являться плоскостью истинного горизонта (плоскость Н), а вертикальная. плоскость, проходящая через отвесную линию и ось вращения Земли—плоскостью истинного меридиана наблюдателя- (плоскость Р). Следует сечения этой плоскостью поверхности Земли укажет на ней положение истинного (географического) меридиана.
Плоскость истинного меридиана наблюдателя пересекается плоскостью истинного горизонта по прямой NS, называемой полуденной линией или линией истинного меридиана наблюдателя. Полуденная линия соответствует направлению на Северный и Южный полюсы, в плоскости истинного горизонта. На этом основании точка истинного горизонта, определяющая направление на север, обозначается N (Nord), а точка, соответствующая направлению на юг,— S (Sud).

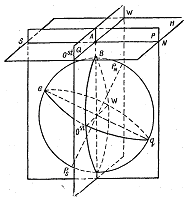
Вертикальная плоскость Q, перпендикулярная плоскости истинного меридиана, называется плоскостью первого вертикала. След от сечения этой плоскостью поверхности Земли представляет собой большой круг, называемый первым вертикалом. Плоскость первого вертикала пересекается с плоскостью истинного горизонта по прямой, которая указывает направление на восток (Оst) (или Е) и на запад (W).
Направления N, Ost (E), S, W называются главными направлениями или румбами в плоскости истинного горизонта. Для каждой точки земной поверхности главные направления занимают вполне определенное и постоянное положение. Исключение составляют географические полюсы, где направление силы тяжести совпадает с осью вращения Земли и всякая вертикальная плоскость будет являться плоскостью истинного меридиана. Для наблюдателя, находящегося на Северном полюсе, любое направление в плоскости истинного горизонта будет являться направлением на Южный полюс (S).
Главными направлениями (N, Оst, S, W) плоскость истинного горизонта делится на четыре равные части— четверти, которые обозначаются сокращенными названиями главных румбов, образующих эти четверти: NOst, SOst, SW, NW —и носят соответствующие им наименования: норд-остовая, зюйд-остовая, зюйд-вестовая и норд-вестовая. Все названия четвертей начинаются с названия нордовой или зюйдовой части меридиана.
Любое направление на поверхности Земли может быть измерено углом в плоскости истинного горизонта между вертикальной плоскостью, принятой за начальную, и плоскостью вертикала, проходящего через место наблюдателя и наблюдаемый объект. За начало счета направлений чаще всего принимается линия истинного меридиана, положение которой для наблюдателя, находящегося в данной точке земной поверхности, остается неизменным.
Для определения направления в плоскости истинного горизонта используются три системы деления горизонта: круговая, полукруговая и четвертная.
В круговой системе весь горизонт делится на 360°. Счет направления ведется от 0 до 360° по ходу часовой стрелки от северной части истинного меридиана наблюдателя.
В полукруговой системе счет направлений ведется как от северной, так и от южной части меридиана наблюдателя в сторону Ost и W в пределах от 0 до 180°. Для направлений в полукруговом счете кроме величины угла обязательно указывается, от какой части истинного горизонта (N или S) и в какую сторону (к Оst или к W) отсчитано данное направление, например: N20°0Ost, S48°W, S54°Ost, N1б5°W.
Чтобы перейти от направлений в полукруговом счете к направлениям в круговом счете, следует:
— при направлениях от N к Оst отбросить буквы наименования, оставив сам угол без изменений; например, угол в полукруговом счете N125° Ost равен углу 125° в круговом счете;
— при направлениях от N к W отбросить буквы наименования и взять численное дополнение заданного угла до 360°; например, направлению N140°W соответствует направление в круговом счете 220°;
— при направлениях от S к Ost отбросить наименование и взять дополнение данного угла до 180°;
— при направлениях от S к W отбросить наименование и к направлению в полукруговом счете, прибавить 180°.
Пусть, например, требуется перевести в круговой счет следующие направления: N270 Ost, S132° Ost, S63°W, N98°W. В круговом счете эти направления соответственно будут: 27°, 48°, 243°, 262°.
В четвертной системе каждая четверть горизонта делится на 90° и отсчет направлений ведется от северной или от южной части меридиана наблюдателя в сторону Ost или W в пределах от 0 до 90°. В этой системе направление показывается наименованием четверти (NОst, SOst, SW, NW) и соответствующим углом, например: NOst30°, NW64°, SOst73°, SW55°. Переход от четвертной системы к круговой осуществляется с соблюдением тех же правил, что и изложенные выше для перехода от полукруговой к круговой системе. Пример соответствия отдельных направлений в различных системах деления горизонта приведен в таблице 1.

Таблица 1

Дата добавления: 2014-12-25