Решение. 1 страница

1) Вектор .

Находим

Итак,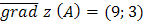

2) Производная функции в точке 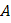по направлению вектора находится по формуле

, где

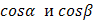– направляющие косинусы вектора .

Находим ,

.

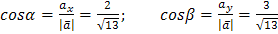Тогда .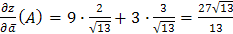

Задача 15. Экспериментально получены пять значений функции при пяти значениях аргумента, которые записаны в таблице:

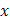
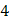
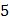
Методом наименьших квадратов найти функцию вида 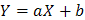, выражающую (аппроксимирующую) функцию . Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции .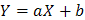

Решение. Найдем необходимые для расчетов суммы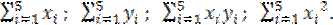

Промежуточные вычисления оформим в виде вспомогательной таблицы.

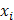
		2,1 3,3 2,9 4,4 5,1	2,1 6,6 8,7 17,6 25,5
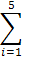
		17,8	60,5

Система нормальных уравнений

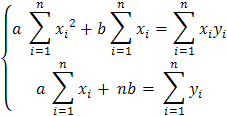
имеет вид .

Ее решение 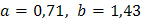дает искомую зависимость: .

Задача 16. Найти полный дифференциал функции .

Решение. Найдем частные производные функции и воспользуемся формулой

.

.

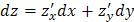Задача 17

1) Найти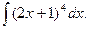

Решение. Воспользуемся заменой переменной, получим

.

2) Найти .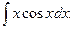

Решение. Применим метод интегрирования по частям

.

3) Найти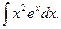

Решение. Применим метод интегрирования по частям дважды

.

4) Найти

Решение. Разложим знаменатель подынтегральной рациональной функции на множители: Правильная дробь разлагается в сумму простейших дробей: 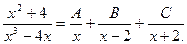Воспользовавшись методом неопределенных коэффициентов, найдем коэффициенты A, В, C. Приведем правую часть равенства к общему знаменателю и приравняем числители: Подставляем корни знаменателя:

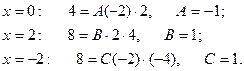
Таким образом, искомое разложение на простейшие дроби имеет вид:

В результате получаем:

.

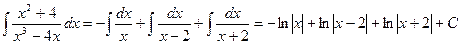5)Найти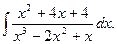

Решение. Разложим знаменатель на множители

.

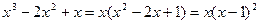Подынтегральная функция разложится на сумму простейших дробей:

Приведем правую часть равенства к общему знаменателю и приравняем числители: 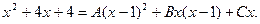Подставляем корни знаменателя:

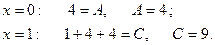
Для нахождения B, приравниваем коэффициенты при , получаем 1= A + B, откуда . Таким образом, искомое разложение на простейшие дроби имеет вид

В результате получаем:

.

6)Найти

Решение. Рациональная дробь – правильная и ее разложение на простейшие дроби имеет вид: 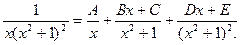Сравнивая числители дробей в обеих частях равенства, получим Имеется только один действительный корень 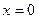, этого достаточно для нахождения только одного коэффициента А:

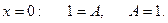
Для нахождения остальных коэффициентов раскроем скобки в правой части равенства и запишем ее в виде многочлена четвертой степени:

Сравнивая коэффициенты при одинаковых степенях x левой и правой частях, получим систему уравнений для нахождения неопределенных коэффициентов

Отсюда находим Искомое разложение имеет вид

Следовательно

Второй и третий интеграл справа находим одинаковой заменой и окончательно получаем

7) Найти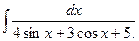

Решение. Подынтегральная функция рационально зависит от и ; применим подстановку , тогда

, ,

и

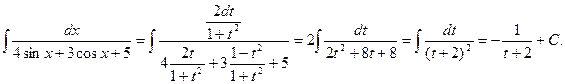
Возвратившись к старой переменной, получим

8)Найти

Решение. Выполним замену переменной Числитель подынтегрального выражения можно представить следующим образом:

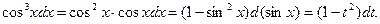
Поэтому имеем

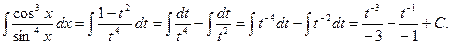
Возвращаясь к переменной , получим

y

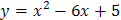Задача 18. Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.

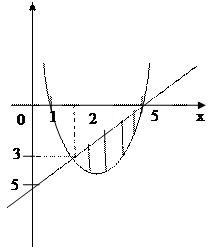Решение. Воспользуемся формулой , где 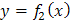– функция, график которой ограничивает фигуру сверху, а 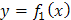– снизу (на отрезке ).

.

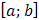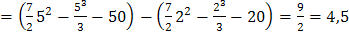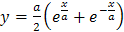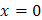Задача 19. Вычислить длину дуги цепной линии от до .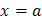

Решение. Длину дуги вычислим по формуле .

Найдем : или . Тогда

Задача 20. Найти общее решение дифференциального уравнения xy’ + 2y = x² и частное решение, удовлетворяющее начальному условию при .

Решение. Полагаем y = u (x) v(x), находим y’ = u’v + uv’. Подставим вместо y и y’ соответствующие выражения в исходное уравнение:

x (u’v + uv’) + 2uv = x², или xu’v + u (xv’ + 2v) = x². (*)

Подберем v = v (x) так, чтобы xv’ + 2v = 0, или , откуда 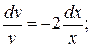интегрируя, имеем или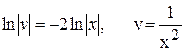

Уравнение (*) примет вид:

u’v = x, или u’ = x, отсюда u’ = x³, 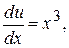du = x³ dx, u =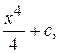

у = u (x) v (x) = 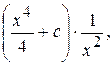или - общее решение.

Найдем частное решение данного уравнения, удовлетворяющее начальному условию при : 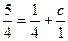, откуда . Таким образом, 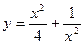- частное решение.

Задача 21. Найти общее решение дифференциального уравнения .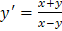

Решение. Поскольку это уравнение однородное то применим подстановку , тогда 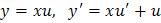. После подстановки в уравнение получим . Разделим переменные: . Интегрируя левую часть равенства по u, а правую – по x, получим:

Вернемся к прежней переменной:

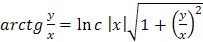. Общий интеграл: .

Задача 22. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям при .

Решение. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Найдем 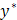– общее решение соответствующего однородного уравнения

. Составим характеристическое уравнение: . Его корни действительные различные, поэтому .

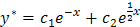Т.к. правая часть неоднородного уравнения и не корень характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде: .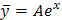

Находим 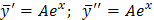. Подставляя в неоднородное уравнение, получим .

Итак, .

Общее решение линейного неоднородного уравнения , поэтому общее решение .

Найдем частное решение, удовлетворяющее начальным условиям .

Т.к. , то имеем систему уравнений для нахождения постоянных 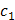и :

.

Итак, искомое частное решение: .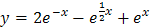

Задача 23. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям .

Решение. Имеем линейное неоднородное уравнение с постоянными коэффициентами. Найдем 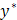– общее решение соответствующего однородного уравнения . Для этого составим характеристическое уравнение . Его корни 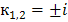комплексные, поэтому .

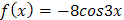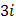Т.к. правая часть неоднородного уравнения и - не корень характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде 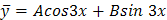. Находим

.

Подставляем в неоднородное уравнение, получим

.

Итак, .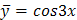

Общее решение линейного неоднородного уравнения , поэтому общее решение .

Найдем частное решение, удовлетворяющее условиям .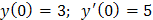

Т.к. , то имеем систему уравнений для нахождения постоянных

.

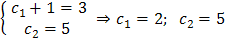Итак, искомое частное решение: .

Задача 24. Исследовать сходимость числового ряда

Решение. Воспользуемся признаком Даламбера:

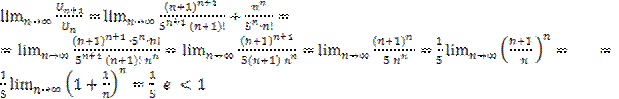, поэтому ряд сходится.

Задача 25. Найти область сходимости степенного ряда .

Решение. Имеем . Находим радиус сходимости

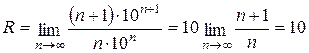, (-10, 10) – интервал сходимости.

Исследуем на сходимость степенной ряд на концах интервала сходимости:

а) при 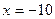получаем числовой ряд , который сходится по признаку Лейбница.

б) при x=10 получаем расходящийся гармонический ряд .

Итак, [-10, 10) - область сходимости.

Задача 26. Написать три первых члена степенного ряда по заданному общему члену 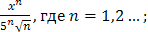найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.

Решение.

Интервал сходимости этого степенного ряда с центром в нуле имеет вид <-R;R>. Радиус сходимости R найдем по формул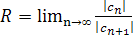е , где – коэффициенты степенного ряда.

Имеем , поэтому =
. Итак, <-5;5> – интервал сходимости.

При имеем ряд , который расходится ( сходится при и расходится при ).

При получаем ряд , который сходится по признаку Лейбница (знакочередующийся ряд, модули членов которого убывают и стремятся к нулю). Итак, [-5;5) – область сходимости данного ряда.

Задача 27. Вычислить определенный интеграл с точностью до 0,001, разложив подинтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Решение. Заменив 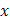на 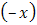в разложении

,

получим .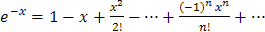

Умножая полученный ряд на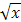

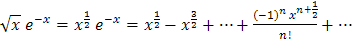
и почленно интегрируя по отрезку 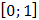, принадлежащему интервалу сходимости ряда 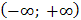, получим

Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность 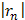, не превышающую первого отброшенного члена (по абсолютной величине), т.е.

.

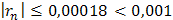Итак,

.

Задача 28. Выразить определенный интеграл в виде сходящегося ряда, используя ряд Маклорена для подинтегральной функции. Найти приближенное значение этого интеграла с точностью до 0,001.

Решение. Заменив 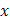на в разложении получим .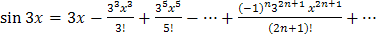

Умножая полученный ряд на

и почленно интегрируя по отрезку , принадлежащему интервалу сходимости ряда 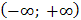, получим

Взяв первые четыре члена разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность 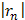, не превышающую первого отброшенного члена (по абсолютной величине), т.е.

.

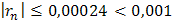Итак, .

Задача 29. Два стрелка стреляют по мишени. Вероятность попадания первым стрелком равна 0.8, вторым – 0.9. Найти вероятность того, что при залпе по мишени попадет только один стрелок.

Дата добавления: 2014-12-26