
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 4 страница. Найдя число 192/8 = 24, мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода
|
|
|
|
Найдя число 192/8 = 24, мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно 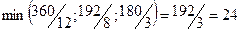 , т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.
, т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.
Следовательно, вектор 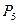 подлежит исключению из базиса. Столбец вектора
подлежит исключению из базиса. Столбец вектора 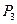 и 2-я строка являются направляющими. Элемент, стоящий на пересечении столбца
и 2-я строка являются направляющими. Элемент, стоящий на пересечении столбца 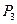 и 2-й строки, называется разрешающим элементом. Составляем таблицу для II итерации (табл. 1.2).
и 2-й строки, называется разрешающим элементом. Составляем таблицу для II итерации (табл. 1.2).
Таблица 1.2
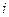
| Базис |
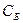
|
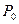
| ||||||
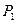
| 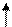 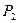
| 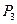
| 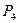
| 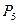
| 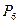
| ||||

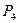
|
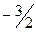
| ||||||||
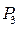
| 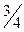
| 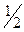
| 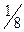
| ||||||
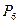
| 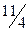
| 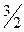
| 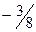
| ||||||
| -2 |
Сначала заполняем строку вектора, вновь введенного в базис, т.е. строку, номер которой совпадает с номером направляющей строки. Здесь направляющей является 2-я строка. Элементы этой строки табл. 1.2 получаются из соответствующих элементов табл. 1.1 делением их на разрешающий элемент (т.е. на 8). При этом в столбце 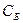 записываем коэффициент
записываем коэффициент 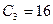 , стоящий в столбце вводимого в базис вектора
, стоящий в столбце вводимого в базис вектора 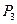 . Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.
. Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.
Для определения остальных элементов табл. 1.2 применяем правило прямоугольника:

 a c
a c
|

 b
b 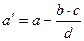 , где
, где 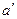 - пересчитанный коэффициент новой таблицы,
- пересчитанный коэффициент новой таблицы,
d – разрешающий элемент,
b, c – элементы, стоящие на диагонали прямоугольника.
Вычислим элементы табл. 1.2, стоящие в столбце вектора 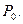 Первый из них находится в 1-й строке этого столбца. Получаем:
Первый из них находится в 1-й строке этого столбца. Получаем:

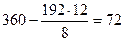 ; записываем его в 1-й строке столбца вектора
; записываем его в 1-й строке столбца вектора 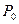 табл. 1.2.
табл. 1.2.
Второй элемент столбца вектора 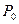 табл. 1.2 был уже вычислен ранее. Вычисляем третий элемент столбца вектора
табл. 1.2 был уже вычислен ранее. Вычисляем третий элемент столбца вектора 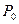 :
: 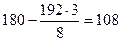 . Число 108 записываем в 3-й строке столбца вектора
. Число 108 записываем в 3-й строке столбца вектора 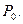 табл. 1.2.
табл. 1.2.
Значение 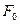 в 4-й строке столбца этого же вектора можно найти двумя способами:
в 4-й строке столбца этого же вектора можно найти двумя способами:
1) по формуле 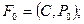 ,т.е.
,т.е. 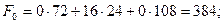
2) по правилу прямоугольника; в данном случае прямоугольник образован числами 0, 192, 8, -16. Этот способ приводит к тому же результату: 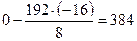 .
.
Аналогично пересчитываем оставшиеся элементы табл. 1 и записываем их в новую табл. 2.
По окончании расчета всех элементов табл. 1.2 в ней получены новый опорный план и коэффициенты разложения векторов 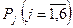 через базисные векторы
через базисные векторы 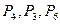 и значения
и значения 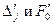 .Как видно из этой таблицы, новым опорным планом задачи является план
.Как видно из этой таблицы, новым опорным планом задачи является план 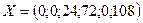 . При данном плане производства изготовляется 24 изделия С и остается неиспользованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора
. При данном плане производства изготовляется 24 изделия С и остается неиспользованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора 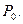 табл. 1.2. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца вектора
табл. 1.2. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца вектора 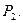 Число
Число 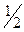 во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и
во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и 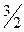 в 1-й и 3-й строках вектора
в 1-й и 3-й строках вектора 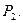 показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия B, а число -2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными словами, если включить в план производства продукции одно изделие В, то это потребует уменьшения выпуска изделия С на
показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия B, а число -2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными словами, если включить в план производства продукции одно изделие В, то это потребует уменьшения выпуска изделия С на 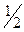 ед. и потребует дополнительных затрат 9 кг сырья I вида и
ед. и потребует дополнительных затрат 9 кг сырья I вида и 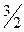 кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и
кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и 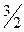 выступают как бы новыми «нормами» затрат сырья I и III вида на изготовление одного изделия В (как видно из табл. 1.1, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.
выступают как бы новыми «нормами» затрат сырья I и III вида на изготовление одного изделия В (как видно из табл. 1.1, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.
Такой же экономический смысл имеют и данные столбца вектора 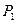 табл. 1.2. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора
табл. 1.2. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора 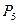 . Число
. Число 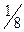 во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на
во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на 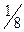 ед. Одновременно потребовалось бы дополнительно
ед. Одновременно потребовалось бы дополнительно 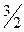 кг сырья I вида и
кг сырья I вида и 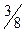 кг сырья III вида. Увеличение выпуска изделий С на
кг сырья III вида. Увеличение выпуска изделий С на 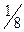 ед. приведет к росту выпуска продукции на 2 руб.
ед. приведет к росту выпуска продукции на 2 руб.
Из изложенного выше экономического содержания данных табл. 1.2 следует, что найденный на II итерации план задачи не является оптимальным. Это видно и из 4-й строки табл. 1.2, поскольку в столбце вектора 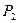 этой строки стоит отрицательное число -2. Значит, в базис следует ввести вектор
этой строки стоит отрицательное число -2. Значит, в базис следует ввести вектор 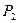 , т. е. в новом плане следует предусмотреть выпуск изделий В. При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется
, т. е. в новом плане следует предусмотреть выпуск изделий В. При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется 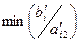 для
для 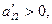 т.е. находим
т.е. находим 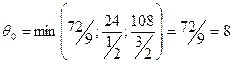 .
.
Следовательно, исключению из базиса подлежит вектор 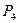 , иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В. Число 9 является разрешающим элементом, а столбец вектора
, иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В. Число 9 является разрешающим элементом, а столбец вектора 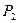 и 1-я строка табл. 1.2 являются направляющими. Составляем таблицу для III итерации (табл. 1.3).
и 1-я строка табл. 1.2 являются направляющими. Составляем таблицу для III итерации (табл. 1.3).
Таблица 1.3
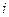
| Базис |
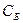
|
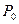
| ||||||
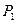
| 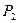
| 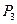
| 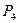
| 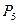
| 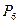
| ||||
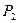
| 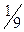
| 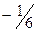
| |||||||
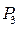
| 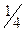
| 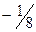
| 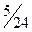
| ||||||
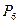
| 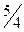
| 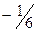
| 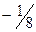
| ||||||
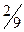
| 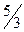
|
В табл. 1.3 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора 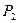 . Элементы этой строки получаем из элементов 1-й строки табл. 1.2 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце
. Элементы этой строки получаем из элементов 1-й строки табл. 1.2 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце 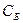 данной строки записываем
данной строки записываем 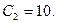
Затем заполняем элементы столбцов векторов базиса и по правилу прямоугольника вычисляем элементы остальных столбцов. В результате в табл. 3 получаем новый опорный план 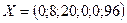 и коэффициенты разложения векторов
и коэффициенты разложения векторов 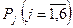 через базисные векторы
через базисные векторы 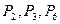 и соответствующие значения
и соответствующие значения 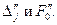
Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку табл. 1.3. В этой строке среди чисел 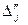 нет отрицательных. Это означает, что найденный опорный план является оптимальным и
нет отрицательных. Это означает, что найденный опорный план является оптимальным и 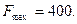
Следовательно, план выпуска продукции, включающий изготовление 8 изделий В и 20 изделий С, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.
Оптимальным планом производства продукции не предусматривается изготовление изделий А. Введение в план выпуска продукции изделий вида А привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора 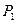 , где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению общей величины стоимости на 5 руб.
, где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению общей величины стоимости на 5 руб.
Ответ: максимальная прибыль от реализации всей продукции составляет 400 руб.
Задача 39
1) На три базы 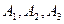 поступил однородный груз в количествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначения
поступил однородный груз в количествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначения 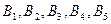 соответственно в количествах 60, 70, 120, 130 и 100 ед. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в следующей таблице:
соответственно в количествах 60, 70, 120, 130 и 100 ед. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в следующей таблице:
Таблица 2.1
| Пункты отправления | Пункты назначения | Запасы | ||||
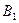
| 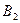
| 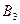
| 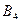
| 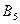
| ||
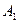
| ||||||
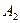
| ||||||
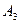
| ||||||
| Потребности |
Найти план перевозок данной транспортной задачи методом северо-западного угла.
Решение. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного 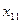 («северо-западный угол») и заканчивается клеткой для неизвестного
(«северо-западный угол») и заканчивается клеткой для неизвестного 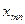 , т. е. идет как бы по диагонали таблицы.
, т. е. идет как бы по диагонали таблицы.
Здесь число пунктов отправления 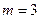 , а число пунктов назначения
, а число пунктов назначения 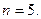 Следовательно, опорный план задачи определяется числами, стоящими в
Следовательно, опорный план задачи определяется числами, стоящими в 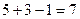 заполненных клетках.
заполненных клетках.
Заполнение таблицы начнем с клетки для неизвестного 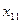 , т. е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Так как запасы пункта
, т. е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Так как запасы пункта 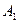 больше, чем потребности пункта
больше, чем потребности пункта 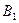 , то полагаем
, то полагаем 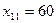 , записываем это значение в соответствующей клетке табл.1и временно исключаем из рассмотрения столбец
, записываем это значение в соответствующей клетке табл.1и временно исключаем из рассмотрения столбец 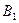 , считая при этом запасы пункта
, считая при этом запасы пункта 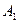 равными 80.
равными 80.
Таблица 2.2
| Пункты отправления | Пункты назначения | Запасы | |||||||||
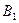
| 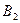
| 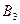
| 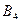
| 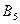
| |||||||
| |||||||||||
| |||||||||||
| |||||||||||
| Потребности |
Рассмотрим первые из оставшихся пунктов отправления 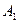 и назначения
и назначения 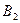 . Запасы пункта
. Запасы пункта 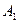 больше потребностей пункта
больше потребностей пункта 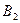 . Положим
. Положим 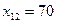 , запишем это значение в соответствующей клетке табл. 2.2 и временно исключим из рассмотрения столбец
, запишем это значение в соответствующей клетке табл. 2.2 и временно исключим из рассмотрения столбец 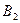 . В пункте
. В пункте 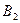 запасы считаем равными 10 ед. Снова рассмотрим первые из оставшихся пунктов отправления
запасы считаем равными 10 ед. Снова рассмотрим первые из оставшихся пунктов отправления 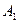 и назначения
и назначения 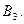 Потребности пункта
Потребности пункта 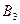 больше оставшихся запасов пункта
больше оставшихся запасов пункта 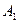 . Положим
. Положим 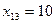 и исключим из рассмотрения строку
и исключим из рассмотрения строку 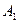 .Значение
.Значение 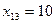 запишем в соответствующую клетку табл. 2.2 и считаем потребности пункта
запишем в соответствующую клетку табл. 2.2 и считаем потребности пункта 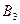 равными 110 ед.
равными 110 ед.
Теперь перейдем к заполнению клетки для неизвестного 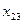 и т. д. Через шесть шагов остается один пункт отправления
и т. д. Через шесть шагов остается один пункт отправления 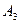 с запасом груза 100 ед. и один пункт назначения
с запасом груза 100 ед. и один пункт назначения 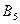 с потребностью 100 ед. Соответственно имеется одна свободная клетка, которую и заполняем, полагая
с потребностью 100 ед. Соответственно имеется одна свободная клетка, которую и заполняем, полагая 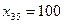 (табл. 2.2). В результате получаем опорный план
(табл. 2.2). В результате получаем опорный план
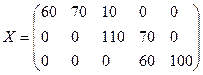
Согласно данному плану перевозок, общая стоимость перевозок всего груза составляет 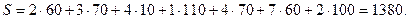
2) Четыре предприятия для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190, 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей
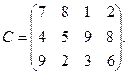
Найти опорный план транспортной задачи методом минимального элемента.
Решение. В методе северо-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запасов первого из оставшихся пунктов отправления. Очевидно, выбор пунктов назначения и отправления целесообразно производить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую-нибудь клетку, отвечающую минимальному тарифу (если таких клеток несколько, то следует выбрать любую из них), и рассмотреть пункты назначения и отправления, соответствующие выбранной клетке. Сущность метода минимального элемента и состоит в выборе клетки с минимальным тарифом. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Поэтому наиболее целесообразно опорный план транспортной задачи находить методом минимального элемента.
Исходные данные задачи запишем в виде табл. 3.1.
Таблица 3.1
| Пункты отправления | Пункты назначения | Запасы | |||||||
| 
| 
| 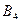
| ||||||
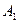
| |||||||||
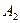
| |||||||||
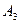
| |||||||||
| Потребности |
Минимальный тариф, равный 1, находится в клетке для переменной 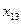 . Положим
. Положим 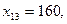 запишем это значение в соответствующую клетку табл. 3.1 и исключим временно из рассмотрения строку
запишем это значение в соответствующую клетку табл. 3.1 и исключим временно из рассмотрения строку 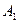 . Потребности пункта назначения
. Потребности пункта назначения 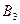 считаем равными 30 ед.
считаем равными 30 ед.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 466; Нарушение авторских прав?; Мы поможем в написании вашей работы!