
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 5 страница. В оставшейся части таблицы с двумя строками и и четырьмя столбцами клетка с наименьшим значением тарифа
|
|
|
|
В оставшейся части таблицы с двумя строками 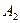 и
и 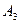 и четырьмя столбцами
и четырьмя столбцами  клетка с наименьшим значением тарифа
клетка с наименьшим значением тарифа  находится на пересечении строки
находится на пересечении строки 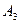 и столбца
и столбца 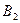 , где
, где  . Положим
. Положим  и внесем это значение в соответствующую клетку табл. 3.1.
и внесем это значение в соответствующую клетку табл. 3.1.
Временно исключим из рассмотрения столбец 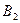 и будем считать запасы пункта
и будем считать запасы пункта 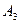 равными 120 ед. После этого рассмотрим оставшуюся часть таблицы с двумя строками
равными 120 ед. После этого рассмотрим оставшуюся часть таблицы с двумя строками  и тремя столбцами
и тремя столбцами  . В ней минимальный тариф
. В ней минимальный тариф  находится в клетке на пересечении строки
находится в клетке на пересечении строки 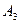 и столбца
и столбца 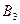 и равен 3. Заполним описанным выше способом эту клетку и аналогично заполним (в определенной последовательности) клетки, находящиеся на пересечении строки
и равен 3. Заполним описанным выше способом эту клетку и аналогично заполним (в определенной последовательности) клетки, находящиеся на пересечении строки 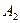 и столбца
и столбца 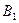 , строки
, строки 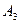 и столбца
и столбца 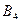 , строки
, строки 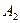 и столбца
и столбца 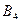 . В результате получим опорный план
. В результате получим опорный план

При данном плане перевозок общая стоимость перевозок составляет

3)Имеются три пункта поставки однородного груза 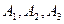 и четыре пункта
и четыре пункта  потребления этого груза. На пунктах
потребления этого груза. На пунктах 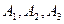 находится груз соответственно в количестве 50, 30 и 10 т. В пункты
находится груз соответственно в количестве 50, 30 и 10 т. В пункты 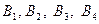 требуется доставить соответственно 30, 30, 10, 20 т груза. Расстояние между пунктами потребления задано следующей матрицей:
требуется доставить соответственно 30, 30, 10, 20 т груза. Расстояние между пунктами потребления задано следующей матрицей:
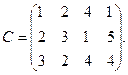
Найти оптимальный план транспортной задачи.
Решение. Сначала, используя метод северо-западного угла, находим опорный план задачи. Этот план записан в табл. 4.1
Таблица 4.1
| Пункты отправления | Пункты назначения | Запасы | |||||||
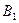
| 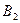
| 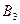
| 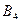
| ||||||
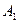
| |||||||||
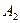
| |||||||||
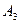
| |||||||||
| Потребности |
Найденный опорный план проверяем на оптимальность. В связи с этим находим потенциалы пунктов отправления и назначения. Для определения потенциалов получаем систему

содержащую шесть уравнений с семью неизвестными. Полагая 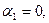 находим
находим 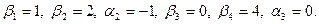 Для каждой свободной клетки вычисляем число
Для каждой свободной клетки вычисляем число  :
:
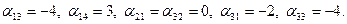
Заключаем найденные числа в рамки и записываем их в каждую из свободных клеток табл. 4.2.
Так как среди чисел 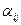 имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел
имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел 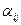 являются
являются  поэтому для данной свободной клетки строим цикл пересчета (табл. 4.2) и производим сдвиг по этому циклу.
поэтому для данной свободной клетки строим цикл пересчета (табл. 4.2) и производим сдвиг по этому циклу.
Таблица 4.2
| Пункты отправления | Пункты назначения | Запасы | |||||||
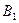
| 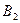
| 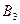
| 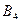
| ||||||
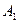
| – | + | |||||||
 -4 -4
|  3 3
| ||||||||
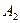
| + | – | |||||||
 0 0
| |||||||||
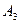
| |||||||||
 -2 -2
|  0 0
|  -4 -4
| |||||||
| Потребности |
Наименьшее из чисел в минусовых клетках равно 10. Клетка, в которой находится это число, становится свободной в новой табл. 4.3. Другие числа в табл. 4.3 получаются так: к числу 10, стоящему в плюсовой клетке табл. 4.2, добавим 10 и вычтем 10 из числа 20, находящегося в минусовой клетке табл. 4.2. Клетка на пересечении строки 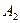 и столбца
и столбца 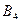 становится свободной.
становится свободной.
После этих преобразований получаем новый опорный план (табл. 4.3).
Таблица 4.3
| Пункты отправления | Пункты назначения | Запасы | |||||||
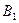
| 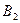
| 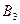
| 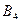
| ||||||
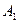
| – | + | |||||||
 -2 -2
| |||||||||
| |||||||||
 0 0
|  -3 -3
|
Окончание табл. 4.3
| 
|  + +
| – | ||||||
| +1 | +3 |  -1 -1
| |||||||
| Потребности |
Этот план проверяем на оптимальность. Снова находим потенциалы пунктов отправления и назначения. Для этого составляем следующую систему уравнений:
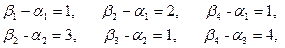
Полагаем 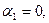 получаем
получаем 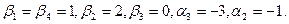 Для каждой свободной клетки вычисляем число
Для каждой свободной клетки вычисляем число 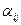 ; имеем,
; имеем,

Таким образом, видим, что данный план перевозок не является оптимальным. Поэтому переходим к новому опорному плану (табл. 4.4).
Таблица 4.4
| Пункты отправления | Пункты назначения | Запасы | |||||||
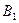
| 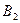
| 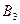
| 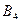
| ||||||
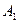
| |||||||||
 -4 -4
| |||||||||
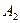
| |||||||||
 0 0
|  -3 -3
| ||||||||
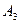
| |||||||||
 -2 -2
|  -4 -4
|  -3 -3
| |||||||
| Потребности |
Сравнивая разности  новых потенциалов, отвечающих свободным клеткам табл. 4.4, с соответствующими числами
новых потенциалов, отвечающих свободным клеткам табл. 4.4, с соответствующими числами  , видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующих чисел
, видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующих чисел  . Следовательно, полученный план
. Следовательно, полученный план
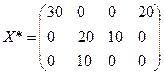
является оптимальным. При данном плане стоимость перевозок

СПИСОК ЛИТЕРАТУРЫ
1. Кудрявцев В.А. Краткий курс высшей математики / В.А. Кудрявцев, Б.П. Демидович. – 6-е изд. – М., 1985.
2. Венцель Е.С. Теория вероятностей / Е.С. Венцель. – М.: Высш. шк.; 1999.
3. Бугров Я.С. Высшая математика: Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский. – Ростов н/Д.: Феникс, 1997.
4. Бугров Я.С. Высшая математика: Дифференциальное и интегральное исчисления / Я.С. Бугров, С.М. Никольский. – Ростов н/Д.: Феникс, 1997.
5. Кузнецов А.В. Высшая математика: Математическое программирование / А.В. Кузнецов, В.А. Сакович, Н.И. Холод. – Минск: Высшая школа, 1994.
6. Сборник задач и упражнений по высшей математике: Мат. программирование: Учеб. пособие / А.В.Кузнецов, В.А. Сакович, Н.И.Холод и др.; Под общей ред. А.В. Кузнецова, Р.А. Рутковского. – Мн. Высш. шк. 2002.
7. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман, Под ред. проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 2003.
8. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 543 с.
9. Шипачев В.С. Высшая математика. Учебник для вузов / В.С. Шипачев. – М.: Высш. шк., 2003.
10. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. – М.: Высш. шк., 2001. – 479 с.
11. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учеб. пособие для студентов вузов / В.Е. Гмурман. – М.: Высш.шк., 2001. – 400 с.
12. Данко П.Е. Высшая математика в упражнениях и задачах. – В 2 ч. Ч. 1, 2. Учеб. пособие для втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: ОНИКС 21 век, Мир и образование, 2003.
13. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов / И.Л. Акулич. – М.: Высш. шк., 1986.
14. Общий курс высшей математики для экономистов: Учебник / Под ред. В.И.Ермакова. – М.: ИНФРА-М., 2001.
15. Хазанова Л.Э. Математические методы в экономике: Учеб. пособие / Л.Э. Хазанова. – М.: БЕК, 2002.
16. Пинегина М.В. Математические методы и модели в экономике / М.В. Пинегина. – М.: Экзамен, 2002.
17. Ефимов Н.В. Краткий курс аналитической геометрии. – 6-12-е изд. / Н.В. Ефимов. – М.: ФИЗМАТЛИТ, 2002.
18. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов / Н.С. Пискунов. – М.: Интеграл Пресс, 2002.
19. Пантелеев А.В. Обыкновенные дифференциальные уравнения в примерах и задачах. Учеб. пособие / А.В. Пантелеев, А.С. Якимова, А.В. Босов. – М.: Высш. шк., 2001.
20. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – 4-е изд. / Д.В. Беклемишев. – М.: Физико-математическая литература, 2002.
21. Гнеденко Б.В. Курс теории вероятностей / Б.В. Гнеденко. – М.: Наука, 2002.
22. Колемаев В.А. Теория вероятностей и математическая статистика / В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский. – М.: Высш. шк., 1991.
23. Бугров Я.С. Высшая математика: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. – Ростов н/Д.: Феникс, 1997.
24. Сборник задач по математике для втузов: Линейная алгебра и основы математического анализа / Под ред. Н.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1986.
25. Сборник задач по математике для втузов: Специальные разделы математического анализа / Под ред. Ефимова Н.В., Б.П. Демидовича. – М.: Наука, 1986.
26. Пантелеев А.В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах: Учеб. пособие / А.В. Пантелеев, А.С. Якимова. – М.: Высш.шк., 2001.
27. Ильин В.А. Высшая математика: Учебник / В.А. Ильин, А.В. Куркина. – М.: ТК Велби, 2002.
28. Кузнецов Ю.Н. Математическое программирование / Ю.Н. Кузнецов, В.И. Кузубов. – М.: Высш. шк., 1980.
29. Минюк С.А. Математические методы и модели в экономике: Учеб. пособие / С.А. Минюк, Е.А. Ровба, К.К. Кузьмич. – Мн.: Тетра Системс, 2002.
30. Колемаев В.А. Теория вероятностей и математическая статистика: Учебник / В.А. Колемаева, Калинина В.Н.; Под ред. В.А. Колемаева. – М.: ИНФРА-М., 1997.
31. Гусак А.А. Высшая математика. – В 2 т. – Т. 1.: Учеб. пособие для студентов вузов / А.А. Гусак. – Мн.: Тетра Системс, 1998. – 544 с.; Т. 2.: Учеб. пособие для студентов вузов. – Мн.: Театра Системс, 1998. –288 с.
32. Гусак А.А. Справочное пособие по решению задач: аналитическая геометрия и линейная алгебра / А.А. Гусак. – Мн.: Тетра системс, 1998. – 288 с.
33. Гусак А.А. Справочное пособие по решению задач: математический анализ и дифференциальные уравнения / А.А. Гусак. – Мн.: Тетра системс, 1998. – 416 с.
34. Гусак А.А. Справочное пособие по решению задач: Теория вероятностей / А.А. Гусак, Е.А. Бришикова. – Мн.: Тетра системс, 1999. – 288 с.
35. Математическое программирование: Программа, методические указания и контрольные задания для студентов заочников инженерно-экономических и экономических специальностей высших учебных заведений / В.Г. Суздаль, Л.Г. Седых, Ю.В. Боровских. – М.: Высш. шк., 1983. – 48 с.
36. Высшая математика: Программа, методические указания и контрольные задания для студентов заочников экономических специальностей высших учебных заведений / Д.П. Полозков. – М.: Высш. шк., 1976. – 55 с.
37. Теория вероятностей и математическая статистика. Методические указания и контрольные задания для студентов специальностей 0608 Бухгалтерский учет, контроль и анализ хозяйственной деятельности и 0717 Экономика, управление в бытовом и жилищно-коммунальном обслуживании, городском хозяйстве. – В 2 ч. / Сост.: В.С. Котанов. – М.: Московский технол. ин-т.
38. Шапкин А.С. Ч. 1. Случайные события и случайные величины М., 1989. – 51 с.; Ч. 2. Математическая статистика. – 41 с.
39. Сборник задач по высшей математике для экономистов: Учеб. пособие / Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2001.
40. Красс М.С. Математика для экономических специальностей: Учебник / М.С. Красс. – М.: Дело, 2002.
41. Красс М.С. Основы математики и ее приложения в экономическом образовании / М.С. Красс, Б.П. Чупрынов. – М.: Дело, 2001.
42. Пантелеев А.В. Методы оптимизации в примерах и задачах: Учеб. пособие / А.В. Пантелеев, Т.А. Летова. – М.: Высш. шк., 2002.
43. Романенко В.К. Сборник задач по дифференциальным уравнениям и вариационному исчислению / В.К. Романенко, Н.Х. Агаханов, В.В. Власов, Л.И. Коваленко. – М.: ЮНИМЕДИАСТАЙЛ, 2002.
Составители: САФИН Рашит Рафаилович
ЛАРИЧЕВА Галина Александровна
БОГДАНОВА Маргарита Анатольевна
«МАТЕМАТИКА»
Учебно-методический комплекс
Часть 3
Методические указания
к выполнению контрольных работ
для студентов всех специальностей и направлений
заочной формы обучения
Технический редактор: С.А. Юдина
Подписано в печать 05.02.12. Формат 60×84 1/16.
Бумага писчая. Гарнитура «Таймс».
Усл. печ. л. 4,59. Уч.-изд. л. 5. Тираж 150 экз.
Цена свободная. Заказ № 42.
Отпечатано с готовых авторских оригиналов
на ризографе в издательском отделе
Уфимской государственной академии экономики и сервиса
450078, г. Уфа, ул. Чернышевского, 145; тел. (347) 241-69-85.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 424; Нарушение авторских прав?; Мы поможем в написании вашей работы!