
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 3 страница
|
|
|
|

| 
| 
| 
| 
| 
| 
| 
| 
|
| 
| 
| ||||||

| 
| 
| 
| 
| ||||

| 
| 
| 
| 
| ||||
| 
| 
| 
| 
| 
| |||
| 
| 
| 
| 
| ||||

| 
| 
| 
| 
| ||||

| 
| 
| 
| |||||

| 
| 
| 
| 
| ||||
| 
| 
| 
| |||||
| 
| 
| 
| 
| 
| 
| 
| 
|
Найдем вспомогательные величины:
 ;
;
 ;
;
 ;
;
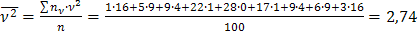 ;
;
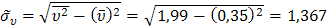 ;
;
 ;
;
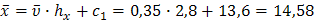 ;
;
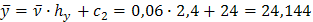 ;
;
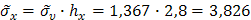 ;
;
 ;
;
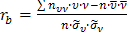 .
.
Для вычисления суммы 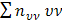 составим таблицу
составим таблицу

| 
| 
| 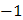
| 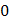
| 
| 
| 
| 
| 
|
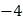
| (-3 -4) | 
| 
| ||||||

| (-6 -6) | (-4 -6) | (-1 -3) | 
| 
| ||||

| (-8 -8) | (-3 -6) | (0 -4) | 
| 
| ||||
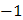
| (-2 -1) | (-6 -6) | (0 -11) | (4 -4) | 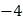
| 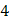
| |||
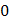
| (-5 0) | (0 0) | (15 0) | 
| 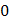
| ||||

| (0 4) | (7 7) | (12 6) | 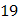
| 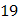
| ||||

| (5 10) | (8 8) | 
| 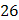
| |||||

| (1 3) | (4 6) | (9 9) | 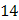
| 
| ||||
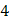
| (2 4) | (6 8) | 
| 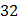
| |||||
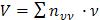
| 
| 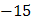
| 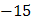
| 
| 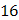
| 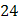
| 
| 
| |

| 
| 
| 
| 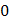
| 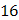
| 
| 
| 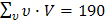
| 
|
Тогда 
Найдем уравнения регрессий:  ;
;
 или
или  ;
;
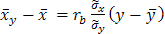 ;
;  или
или
 . Для построения диаграммы рассеивания найдем групповые средние:
. Для построения диаграммы рассеивания найдем групповые средние: 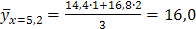 ;
; 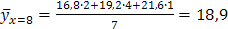 ;
;
 ;
; 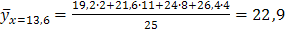 ;
;
 ;
;
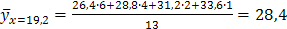 ;
; 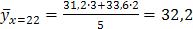 ;
;  ;
;
 ;
;  ;
;
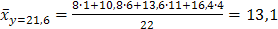 ;
;  ;
;
 ;
;  ;
;
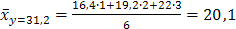 ;
;  .
.
Изобразим диаграмму рассеивания (точки) и графики уравнений регрессии.

Задача 37. Найти максимальное значение линейной функции 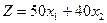 при ограничениях
при ограничениях

Решение. Построим многоугольник решений. Для этого в системе координат  на плоскости изобразим граничные прямые
на плоскости изобразим граничные прямые

Взяв какую-нибудь, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство (эти полуплоскости на рисунке показаны стрелками). Многоугольником решений данной задачи является ограниченный пятиугольник ОАВСD.
Для построения прямой  строим радиус-вектор
строим радиус-вектор  = (50;40)=10 (5;4) и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора
= (50;40)=10 (5;4) и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора  . Из рис. 1.3 следует, что опорной по отношению к многоугольнику решении эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых
. Из рис. 1.3 следует, что опорной по отношению к многоугольнику решении эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых 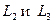 . Для определения её координат решим систему уравнении
. Для определения её координат решим систему уравнении
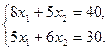
Оптимальный план задачи:  Подставляя значения
Подставляя значения 
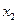 в линейную функцию, получаем
в линейную функцию, получаем 


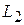 8
8

А
 4
4


0 D 5 
Таким образом, для того чтобы получить максимальную прибыль в размере 260,3 руб., необходимо запланировать производство 3,9 ед. продукции 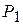 и 1,7 ед. продукции
и 1,7 ед. продукции 
Задача 38. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. При этом на изготовление единицы изделия вида А расходуется 18 кг материала первого вида, 6 кг материала второго вида и 5 кг материала третьего вида. На изготовление единицы изделия вида  расходуется 15 кг материала первого вида, 4 кг материала второго вида, 3 кг материала третьего вида. На изготовление единицы изделия вида C расходуется 12 кг материала первого вида, 8 кг материала второго вида, 3 кг материала третьего вида. На складе фабрики имеется всего материала первого вида 360 кг, материала второго вида 192 кг, материала третьего вида 180 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 9 руб., продукции вида В прибыль составляет 10 руб., продукции вида С прибыль составляет 16 руб.
расходуется 15 кг материала первого вида, 4 кг материала второго вида, 3 кг материала третьего вида. На изготовление единицы изделия вида C расходуется 12 кг материала первого вида, 8 кг материала второго вида, 3 кг материала третьего вида. На складе фабрики имеется всего материала первого вида 360 кг, материала второго вида 192 кг, материала третьего вида 180 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 9 руб., продукции вида В прибыль составляет 10 руб., продукции вида С прибыль составляет 16 руб.
Определить максимальную прибыль от реализации всей продукции видов А, В и С. Решить задачу симплекс-методом.
Решение. Запишем данные задачи в таблицу.
| Вид сырья | Нормы затрат сырья (кг) на одно изделие вида | Общее количество сырья (кг) | ||
| А | В | С | ||
| I | ||||
| II | ||||
| III | ||||
| Прибыль от реализации единицы продукции |
Составим математическую модель задачи. Введем новые переменные:
 количество выпускаемых изделий вида А;
количество выпускаемых изделий вида А;
 количество выпускаемых изделий вида В;
количество выпускаемых изделий вида В;
 количество выпускаемых изделий вида С.
количество выпускаемых изделий вида С.
Так как на 1 изделие вида А предприятие расходует 18 кг сырья первого вида, то на производство общего количества продукции вида А предприятию потребуется  кг того же материала. Соответственно для производства всей продукции вида В и С предприятию потребуется
кг того же материала. Соответственно для производства всей продукции вида В и С предприятию потребуется  кг и
кг и 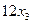 сырья первого вида соответственно. Поскольку расходы на производство не должны превышать общего количества сырья имеющегося на складе, то при изготовлении
сырья первого вида соответственно. Поскольку расходы на производство не должны превышать общего количества сырья имеющегося на складе, то при изготовлении  единиц изделий вида А,
единиц изделий вида А,  единиц изделий вида В и
единиц изделий вида В и 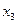 единиц изделий вида С должно быть израсходовано не более 360 кг сырья первого вида. Таким образом, все выше сказанное можем записать в виде неравенства:
единиц изделий вида С должно быть израсходовано не более 360 кг сырья первого вида. Таким образом, все выше сказанное можем записать в виде неравенства:

Аналогично, при затратах, на производство продукции вида А, В и С, сырья второго и третьего сорта предприятие должно учитывать количество данного сырья, имеющегося на складе. Т.е. необходимо выполнение следующих неравенств: 
При этом так как количество изготовляемых изделий не может быть отрицательным, то
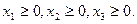
Далее, если будет изготовлено  единиц изделий вида А,
единиц изделий вида А,  единиц изделий вида В и
единиц изделий вида В и 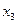 единиц изделий вида С, то прибыль от их реализации составит
единиц изделий вида С, то прибыль от их реализации составит 
Таким образом, приходим к следующей математической задаче:
 (1)
(1)
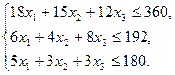 (2)
(2)
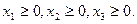
среди всех неотрицательных решений системы неравенств (2) требуется найти такое, при котором функция (1) принимает максимальное значение.
Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений
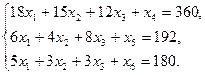
Эти дополнительные переменные означают не используемое при данном плане производства количество сырья того или иного сорта (например, 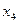 - неиспользуемое количество материала I вида).
- неиспользуемое количество материала I вида).
Преобразованную систему уравнений запишем в векторной форме:

где  ;
; 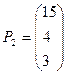 ;
; 
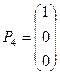 ;
; 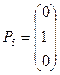 ;
; 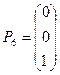 ;
;  .
.
Поскольку среди векторов 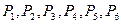 имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план Х=(0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов
имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план Х=(0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов 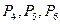 , которые образуют базис трехмерного векторного пространства.
, которые образуют базис трехмерного векторного пространства.
Составляем симплексную таблицу для I итерации (табл. 1.1). В столбец 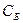 записываем коэффициенты при базисных векторах в целевой функции. Коэффициенты 4-й строки вычисляются по формулам:
записываем коэффициенты при базисных векторах в целевой функции. Коэффициенты 4-й строки вычисляются по формулам:  и проверяем исходный опорный план на оптимальность:
и проверяем исходный опорный план на оптимальность:
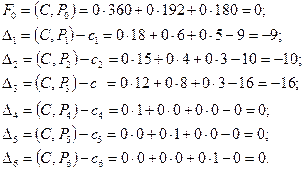
Таблица 1.1
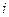
| Базис |
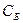
|
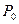
| |||||||
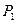
| 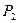
|  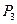
| 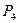
| 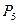
| 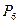
| |||||
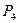
|  360 360
| |||||||||
 
|
| |||||||||
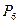
| ||||||||||
| -9 | -10 | -16 |
Как видно из табл. 1.1, значения всех основных переменных  равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.
равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.
Это видно и из 4-й строки табл. 1.1, так как в ней имеется три отрицательных числа:  . Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции. Так, число -9 означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по одному изделию В и С, то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число
. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции. Так, число -9 означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по одному изделию В и С, то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число 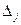 стоит в 4-й строке столбца вектора Р3. Следовательно, в базис введем вектор
стоит в 4-й строке столбца вектора Р3. Следовательно, в базис введем вектор 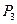 . Определяем вектор, подлежащий исключению из базиса. Для этого находим
. Определяем вектор, подлежащий исключению из базиса. Для этого находим  для
для 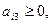 т.е.
т.е. 
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 446; Нарушение авторских прав?; Мы поможем в написании вашей работы!