Центрально-растянутые и центрально-сжатые элементы

РАСЧЕТ ЭЛЕМЕНТОВ НА ОСЕВЫЕ СИЛЫ И ИЗГИБ

5.1 (5.1). Согласно требованиям [1] в расчетах стальных конструкций разрешается использовать два вида расчетных сопротивлений - по пределу текучести R_y и по временному сопротивлению Р_u. При этом в расчетах необходимо учитывать значения отношений R_u/R_y, которые изменяются в пределах от 1,17 до 1,70. Кроме того, следует также различать элементы, не ослабленные и ослабленные отверстиями для болтов. Эти особенности работы стали отражены в [1] и были учтены при формулировке требований СНиП II-23-81* по расчету на прочность, разъяснение которых приводится в пп. 5.2-5.4 настоящего Пособия.

5.2 (5.1). При проверке прочности центрально растянутых элементов с ослаблением сечений отверстиями для болтов не более 15 % в общем случае должны быть выполнены следующие условия

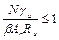; (13)

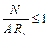, (14)

где g_и - коэффициент, принимаемый согласно СНиП II-23-81*;

b - коэффициент, принимаемый свыше 1,0 [11];

A_n - площадь сечения “нетто”;

R_u и R_y - расчетные сопротивления, принимаемые согласно СНиП II-23-81*;

А - площадь сечения „брутто".

Условие равнопрочности по формулам (13) и (14) для центрально-растянутых элементов получит вид

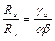, (15)

где a = A_n / A.

Из формулы (15) следует: если R_u / R_y > g_u /(ab), решающей является проверка по формуле (14); в противном случае - по формуле (13).

При a = 0,85 и b = 1,1 [11] следует, что при R_u / R_y > 1,39 достаточно выполнить проверку по формуле (14), если R_u/R_y < 1,39, то необходима проверка по двум формулам (13) и (14).

5.3 (5.1). При ослаблении сечений отверстиями для болтов свыше 15 % формула (13) остается без изменения, а формула (14) получит вид

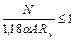, (16)

где 1,18 aА - условная площадь, вводимая в расчет при ослаблении сечения свыше 15 % (см. СНиП П-23-81*).

Из условия равнопрочности при проверках по формулам (13) и (16) имеем

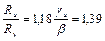. (17)

5.4 (5.1). Для упрощения практических расчетов в СНиП П-23-81* расчетные формулы (13), (14) и (16) приведены к одной формуле с введением соответствующего коэффициента условий работы g_с:

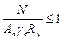. (18)

Коэффициент условий работы g_с определен из сопоставления формул (13), (14) и (16) с формулой (18).

Для большинства наиболее широко применяемых углеродистых сталей с отношением R_u / R_y > 1,39 находим:

при a ³ 0,85 g_с = 1/ a;

” 0,75 £ a < 0,85 g_с = 1,18.

Для сталей с отношением R_u / R_y < 1,39

.

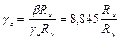При наиболее вероятном ослаблении сечения отверстиями для болтов от 8 до 25 % (a = 0,92-0,75) и R_u / R_y > 1,39 g_с = 1,09-1,18. При R_u / R_y < 1,39 g_с = 0,99-1,18; при этом меньшее значение g_с соответствует R_u / R_y = 1,17, что выполняется для двух марок сталей 12Г2СМФ и 12ГН2МФАЮ, приведенных в СНиП II-23-81*.

С учетом изложенного в СНиП II-23-81* приняты g_с = 1,1 для сталей с пределом текучести sу £ 440 МПа (4500 кгс/см²); g_с = 1,0 - для сталей с пределом текучести s_у > 440 МПа (4500 кгс/см²).

С целью упрощения расчетов на прочность сечений, ослабленных отверстиями для болтов, указанные значения коэффициентов g_с приняты и для других видов напряженно-деформированных состояний элементов конструкций (сжатие, изгиб, сжатие или растяжение с изгибом; см. поз. 6-8 табл. 6* СНиП П-23.81*).

5.5. При расчете на прочность центрально-сжатых элементов необходимо учитывать особенности работы стали на сжатие (см. п. 4.8). В частности, расчет на прочность центрально-сжатых элементов с соединениями на болтах класса точности А допускается выполнять как для неослабленных элементов [1].

5.6 (5.2). Работа растянутых элементов стальных конструкций после достижения металлом предела текучести при R_u / R_y > g_и = 1,3 допускается в ограниченных случаях, когда при значительных деформациях конструкций не нарушается их нормальная эксплуатация. К таким конструкциям относятся, как правило, отдельные листовые конструкции, в основном, с равномерным распределением напряжении (например, листовые настилы, некоторые виды трубопроводов и резервуаров и т. п.). Учитывать работу стали после достижения предела текучести в каждом конкретном случае необходимо на основе опыта проектирования и эксплуатации соответствующего типа конструкций.

5.7. Требования по проверке устойчивости центрально-сжатых стержней установлены в СНиП II-23-81* на основе расчета внецентренно-сжатых стержней с учетом влияния формы сечения, начального искривления оси, случайного эксцентриситета сжимающей силы, а также соединительных элементов (для сквозных стержней).

Начальные искривления или случайные эксцентриситеты приняты в соответствии с допускаемыми отклонениями, установленными в нормах на изготовление стальных конструкций [8].

При решении поставленной задачи был рассмотрен внецентренно-сжатый стержень, схема которого приведена на рис. 3, а. При этом решение выполнялось в предположении малости перемещений по деформированной схеме с учетом пластических деформаций, а значение расчетной несущей способности принято равным предельному значению сжимающей силы N_u, которая может быть воспринята элементом (рис. 3, б). Форма изогнутой оси принималась по полуволне синусоиды.

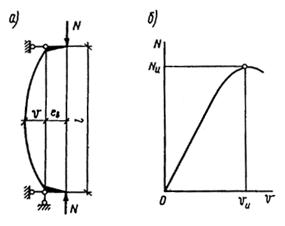
Рис. 3. К расчету сжатых стержней

а - расчетная схема; б - кривая состояния равновесия

5.8 (5.3). В СНиП II-23-81* методика практических расчетов центрально-сжатых элементов приведена с использованием коэффициентов устойчивости при центральном сжатии j (коэффициентов продольного изгиба), которые вычислены с учетом рекомендаций п. 5.7 настоящего Пособия в зависимости от условной гибкости 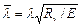и приняты равными j = N_u /(a R_y).

При вычислении значений коэффициентов j типы поперечных сечений сжатых элементов принимались в соответствии с табл. 73 СНиП П-23-81*, а начальные несовершенства е_b - по формуле

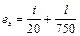, (19)

где i - радиус инерции сечения;

l - расчетная длина элемента.

При нормировании коэффициентов j определялась также критическая сила упругих идеальных стержней по методу Эйлера. Окончательные значения коэффициентов j принимались наименьшими из двух: вычисленных с учетом начальных несовершенств или по методу Эйлера с введением коэффициента надежности g_е = 1,3 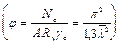. Это было сделано для ограничения прогибов сжатых стержней при относительно больших гибкостях, когда влияние начальных несовершенств, определяемых по формуле (19), становилось несущественным.

Полученные таким образом значения коэффициентов j для различных форм поперечных сечений были осреднены и аппроксимированы с помощью формул (8)-(10) СНиП II-23-81*, на основании которых для различных значений расчетных сопротивлений R_y была составлена табл. 72 СНиП II-23-81*.

Анализ значений коэффициентов j позволяет использовать в расчетах и более простые приближенные зависимости (с точностью до 1,5 %) следующего вида:

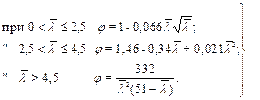(20)

Значения j, полученные по формулам (20), приведены в табл. 11.

Таблица 11

Условная гибкость	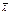Значения j×1000 для элементов из стали с пределом текучести sу, МПа (кгс/см^2)
	до 390(4000)	св. 390(4000)
		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9		0,5
						527'

Примечание. Указанные значения коэффициентов j для элементов из стали с пределом текучести до 390 МПа (4000 кгс/см²) определены по формулам (20), свыше 390 МПа (4000 кгс/см2) - по разд. 5 СНиП II-23-81* при s_у = 430 МПа (4400 кгс/см²).

5.9 (5.5). В основу проверки изгибно-крутильной формы потери устойчивости тонкостенных стержней принята теория В. З. Власова.

В общем случае условие потери устойчивости шарнирно опертого центрально-сжатого упругого тонкостенного стержня имеет вид

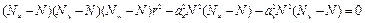, (21)

где ;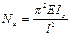

;

;

,

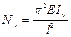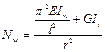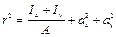здесь a_х и а_у - координаты центра изгиба относительно осей соответственно х-х и у-у.

Для стержня с одной осью симметрии у-у (см. рис. 1 СНиП II-23-81*) а_y = 0, при этом из формулы (21) получим

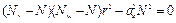. (22)

Разделив на N_y N_w r² все члены уравнения (22), получим

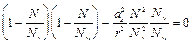. (23)

Введем обозначения с = N / N_y; d = N_y / N_w [12]. С учетом этих обозначений из формулы (23) получим

(1 - с)(1 - сd) - с²b² = 0, (24)

где .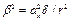

Из уравнения (24) находим

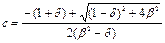. (25)

После простых преобразований зависимости (25) получим

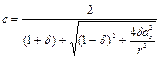. (26)

В практических расчетах по формуле (26) учитывается частичное стеснение депланации опорных сечений введением коэффициента 2 в первый член числителя формулы для N_w [см. формулу (21)], чем приближенно оцениваются фактические условия в узлах стержневых конструкций. В окончательном виде с использованием безразмерных величия эта формула приведена в СНиП II-23-81* под номером (12).

Формула (11) СНиП II-23-81* основана на предположении, что соотношение критических сил при работе элемента за пределом упругости принято таким же, как при работе его в пределах упругости.

5.10 (5.5). Пример расчета центрально-сжатого тонкостенного стержня П-образного сечения (см. рис. 1, а СНиП II-23-81*) с параметрами b = b/h = 0,5 и h/t = 15.

Площадь А и моменты инерции сечения I_x и I_у равны:

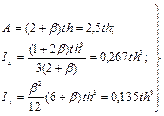(27)

Величины, входящие в формулу (12) СНиП II-23-81*, равны:

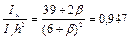; (27)

;

;

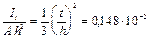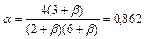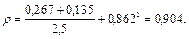
Значения коэффициентов с для различных гибкостей l_у приведены в табл. 12, в которой обозначения приняты в соответствии с формулой (12) СНиП II-23-81*.

Таблица 12

lу	m	16 а^2 / m	d	с	lх
	7,945	1,496	0,455	0,716	28,4
	8,407	1,414	0,430	0,728	42,7
	9,054	1,313	0,399	0,743	56,8
	9,885	1,203	0,367	0,759	71,1
	10,901	1,091	0,332	0,778	85,3

5.11 (5.6). Влияние податливости соединительных элементов на снижение жесткости сквозного сжатого стержня в расчетах приближенно учитывается введением приведенной гибкости l_ef, превышающей гибкость стержня l_у = I_y / i_y, вычисленную по геометрической длине и радиусу инерции 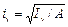(где I_y - момент инерции сечения сквозного стержня относительно свободной оси у-у, см. табл. 7, тип сечения 1, СНиП II-23-81*).

При достаточно большом числе панелей (свыше 8) из решения задачи устойчивости шарнирно опертого идеально упругого сквозного стержня (рис. 4) коэффициент приведенной длины получен в следующем виде [13]:

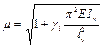, (28)

где g₁ = d/l_b - угол сдвига, зависящий от типа соединительных элементов.

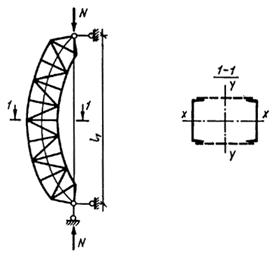
Рис. 4. Шарнирно опертый сквозной стержень

Формулы для определения g₁ и m при различных схемах соединительных элементов, полученные по правилам определения перемещений в рамных и стержневых системах [13], приведены в табл. 13. Для схем решеток типа 3-5 в соответствии с рис. 2 СНиП II-23-81*имеем

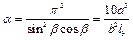. (29)

Для схемы решетки типа 2 получим

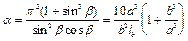. (30)

При подстановке значений a в формулы табл. 13 получим формулы, приведенные в табл. 7 СНиП II-23-81*. Следует отметить, что формулы табл. 13 в ряде случаев являются более строгими, чем приближенные формулы СНиП II-23-81*, применение которых, однако, существенно не влияет на конечные результаты.

5.12 (5.6). Формулы табл. 13 могут быть использованы при определении l_еf для четырехгранного сквозного стержня с подстановкой в них соответствующих геометрических характеристик всего стержня и его отдельных ветвей. Однако результаты экспериментальных исследований четырехгранных стержней с гибкостями g = 20-40 из стали с пределом текучести s_у = 250-278 МПа (2550-2830 кгс/см²) показывают, что такой расчет в связи с наличием начальных несовершенств приводит к завышенным значениям вычисленных предельных нагрузок. В связи с этим в СНиП II-23-81* предлагаются условные формулы (15), (18) и (21), в которые одновременно входят геометрические характеристики элементов стержня для обеих плоскостей потери устойчивости. Сравнение теоретических и экспериментальных данных показывает в этом случае достаточно удовлетворительное соответствие результатов.

5.13 (5.6). Формулы табл. 7 СНиП II-23-81* (тип сечения 3) для определения l_ef для трехгранных сквозных стержней основаны на рассмотрении их потери устойчивости в плоскостях х-х и у-у в предположении неизменности расстояний между ветвями стержня при изгибе.

5.14 (5.6). Формулы табл. 13 настоящего Пособия получены без учета влияния начальных несовершенств и продольных сил в ветвях на значение угла сдвига g₁. В связи с этим в СНиП П-23-81* введены ограничения на значения гибкостей отдельных ветвей.

Для стержней с планками гибкость l_b отдельной ветви, при которой влияние указанных факторов несущественно, составляет 40.

При большем значении l_b формулы для g₁ и m необходимо уточнять заменой выражений (1 + 2 n) и (1 + п) соответственно на (1/ b + 2 n) и (1/ b + n), где 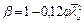(здесь j - коэффициент, вычисляемый для стержня по приведенной гибкости l_ef).

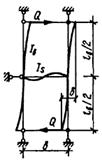
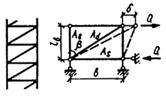
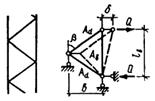
Таблица 13

№ п.п.	Схема соединительных элементов	Формулы для определения g1 и m при числе плоскостей соединительных элементов
		одной	двух
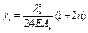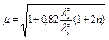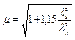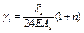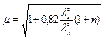		; . При n £ 0,2 ,	; . При n £ 0,2
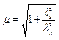
		здесь 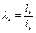; ; 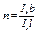Ib - момент инерции сечения пояса; Is - момент инерции сечения одной планки.
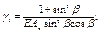
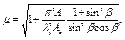
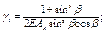
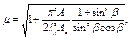
		A-d здесь и в поз. 3-5 принято: 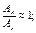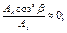A = 2Ab; Ad - площадь сечения одного раскоса; А - площадь сечения всего стержня.

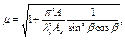
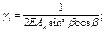
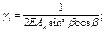
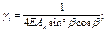
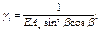
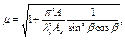
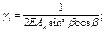
5.15 (5.6). При расчете сквозных решетчатых стержней начальные несовершенства обычно учитываются коэффициентом j в формуле (7) СНиП II-23-81* на стадии подбора сечения всего стержня и проверки устойчивости его отдельных ветвей. В то же время имеются работы ^{1, 2}, в которых показано, что на несущую способность сквозного стержня с решетками существенное влияние оказывают увеличение гибкости панели, а также начальные искривления стержня и отдельных панелей. В связи с этим в п. 5.6 СНиП II-23-81* введены ограничения на значения гибкостей отдельных ветвей между узлами.

______________

¹ Корчак М. Д. О влиянии начальных искривлений пояса на устойчивость решетчатого стержня // Совершенствование и развитие норм проектирования стальных строительных конструкций: Сб. науч. тр. ЦНИИСКа им. Кучеренко. - М., 1981.-С. 119-127.

² Горев В. В., Путилин В. М. О несущей способности и деформативности сжатых сквозных стержней // Строит. механика и расчет сооружений. - 1976. - № 3. - С. 34-37.

В ряде случаев при l_b £ 120 эти ограничения согласно СНиП II-23-8-1* могут быть сняты. При этом требуется выполнить расчет сквозного стержня по деформированной схеме, которую можно учесть приближенным практическим способом расчета, существо которого сводится к следующему:

если гибкость отдельной ветви на участке между узлами 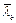³ 3,2, то расчетное сопротивление при проверке сквозного стержня с решетками по формулам (7) или (51) СНиП II-23-81* может быть принято равным j_bR_y (правые части этих формул будут равны j_bR_yg_c), здесь j_b - коэффициент продольного изгиба для отдельной ветви, расчетную гибкость которой можно принять 0,7 l_b; коэффициенты j и j_е в формулах (7) и (51) СНиП II-23-81* необходимо принимать соответственно по табл. 72 и 75 СНиП II-23-81* при указанном расчетном сопротивлении j_bR_y в зависимости от l_ef и ;

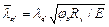при 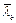£ 2,5 значение j принимается равным 1,0, а в интервале 2,5 < 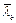< 3,2 - по линейной интерполяции между 1,0 и значением j_b при 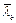= 3,2.

Коэффициент расчетной длины m_b = 0,7 при l_b приближенно учитывает взаимодействие ветви колонны с элементами решетки, а также вероятность одновременного совпадения расчетных значений начальных несовершенств для всего стержня и отдельной панели ветви.

5.16 (5.7). Соединение составных стержней вплотную или через прокладки обеспечивает совместную работу составляющих его элементов и равномерное распределение между ними продольной силы.

Для сжатых стержней длина участка между соединениями равна 401, что соответствует гибкости l_b = 40 в сквозных стержнях с планками. При этом влияние продольной силы на деформирование элементов, составляющих стержень, несущественно (см. п. 5.14 настоящего Пособия).

5.17 (5.8*). Условная поперечная сила Q_fic определяется как проекция продольной сжимающей силы N на ось, перпендикулярную изогнутой оси шарнирно опертого внецентренно-сжатого с эксцентриситетом е_b стержня сквозного сечения, имеющего начальное искривление v_b, в его предельном состоянии (рис. 5) и вычисляется по формуле

Q_fic = N_u sin a» N_u а. (31)

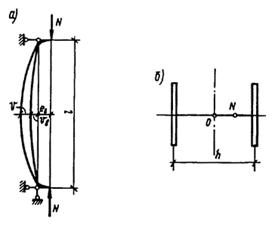
Рис. 5. К определению условной поперечной силы

а - изогнутая ось стержня; б - идеализированное сечение

Для синусоидальной формы начального искривления и изогнутой оси стержня получим

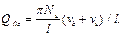(32)

Для вычисления N_u и v_u были определены предельные параметры внецентренно-сжатого стержня идеализированного сечения, состоящего из двух одинаковых полок, связанных между собой жесткой связью (см. рис. 5, б). Влияние решетки на предельное значение N_u учитывалось введением приведенной гибкости l_ef по формуле (17) СНиП II-23-81*.

Полученные значения Q_fic для различных R_y и l аппроксимированы в СНиП II-23-81* приближенной зависимостью

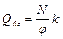, (33)

которая учитывает возможность недонапряжения сквозного стержня в плоскости соединительных элементов; здесь k = 7,15 × 10^-6 .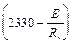

Значения множителя k при N/j в правой части формулы (33) для различных значений расчетных сопротивлений R_y и Е = 2,06 - 10⁵ МПа приведены в табл. 14.

Таблица 14

Ry, МПа(кгс/см^2)	k	Ry, МПа(кгс/см^2)	k
210(2150)	0,0097	330(3350)	0,0122
230(2350)	0,0103	350(3550)	0,0125
250(2550)	0,0108	370(3750)	0,0127
270(2750)	0,0112	400(4100)	0,0130
300(3050)	0,0118	500(5100)	0,0137

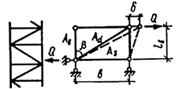
5.18 (5.10). Для определения дополнительных усилий в раскосах перекрестной решетки с целью учета влияния обжатия поясов в сквозных стержнях рассматривается один раз статически неопределимая система, схема которой приведена на рис. 6, а. Разрез одного из раскосов дает основную систему, схемы нагружения которой показаны на рис. 6, б, в.

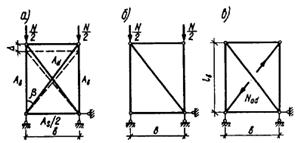
Рис. 6. К расчету перекрестной решетки

а - расчетная схема; б - основная система; в - дополнительное усилие в раскосе

Из решения рассматриваемой задачи получено дополнительное усилие, возникающее в раскосах

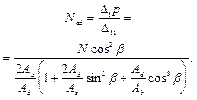(34)

Принимая A_d / A_s» 1 и A_d cos³ b / A_b» 0, можно получить формулу (26) СНиП II-23-81*.

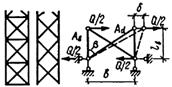
Принимая обозначения s_аd = N_ad/A_d и s_n = N_b / A_b = N / A, получим

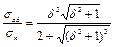, (35)

где d = l_b/b.

Значения отношения s_ad/s_n для различных d приведены в табл. 15.

Таблица 15

d	0,5	0,6	0,8	1,0	1,2	1,4	1,6	1,8
sad/sn	0,082	0,117	0,200	0,293	0,396	0,475	0,554	0,620

Получаемое таким образом дополнительное усилие в раскосах от обжатия поясов стержня сжимающей силой необходимо прибавить к усилию в раскосах от условной (или фактической) поперечной силы Q.

5.19 (5.11). Расчет стержней, предназначенных для уменьшения расчетной длины сжатых элементов, необходимо выполнять на усилие, равное Q_fic и определяемое с использованием данных табл. 14 и формулы (33) в зависимости от продольной силы N и коэффициента продольного изгиба j для основного подкрепляемого элемента.

Расчет распорок, предназначенных для уменьшения расчетной длины колонн в направлении вдоль здания (из плоскости рам), при наличии нагрузок от мостовых кранов допускается выполнять на усилие, определяемое по формуле (33), в которой значение N принимается равным сумме продольных сил в двух соседних колоннах.

Дата добавления: 2014-12-26