
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изгибаемые элементы
|
|
|
|
5.20 (5.14*). В балках, рассчитываемых в пределах упругих деформаций, необходимо проверять прочность стенки при сложном напряженном состоянии путем определения обобщенного напряжения (интенсивности напряжений) на основе энергетической теории прочности по формуле (33) СНиП II-23-81*. Обобщенное напряжение, вычисляемое по этой формуле, сравнивается с расчетным сопротивлением, увеличенным на 15 %, что предполагает развитие локальных неупругих деформаций в стенке.
Указанный расчет необходимо выполнять в первую очередь для проверки стенок двутавровых балок в месте соединения стенки с верхним поясом. При этом в стенках разрезных балок напряжения sx и sу обычно имеют одинаковые знаки, в то время как в сечениях у опор неразрезных балок эти напряжения могут иметь разные знаки, что необходимо учитывать при пользовании формулой (33) СНиП II-23-81*.
5.21 (5.15). Для определения критических напряжений jbRy при потере устойчивости балок двутаврового сечения с двумя осями симметрии, изгибаемых в плоскости стенки, были использованы результаты работ С. П. Тимошенко [13], которые для практических расчетов представлены в СНиП II-23-81* в виде формул (34) и (174). Необходимо подчеркнуть, что в работе [13] исследовались идеальные упругие балки. Для расчета реальных стальных балок в формуле (34) СНиП II-23-81* влияние начальных несовершенств (в частности, начального искривления оси балки в плоскости наименьшей жесткости) учтено при выводе формул для коэффициента Y, а также введением коэффициента условий работы gс (см. поз. 4 табл. 6* СНиП II-23-81*).
Коэффициенты в табл. 77 СНиП II-23-81* приведены для случая шарнирного опирания в плоскости наименьшей жесткости и свободной депланации концов расчетного участка балки.
Значения Y вычислены в предположении, что Iу/Iх £ 1. Если отношение Iу/Iх не очень мало, то значения Y следует умножать на  .
.
Для балок двутаврового сечения с одной осью симметрии коэффициенты j1 и j2, определяемые по формулам (177) и (178) СНиП II-23-81*, были получены в работе [14] на основе использования уравнений В. З. Власова при указанных граничных условиях.
5.22 (5.15). Для случая, когда критические напряжения при потере устойчивости балок превышают предел пропорциональности, методика расчета разработана на основе исследования соотношения между критическим напряжением неограниченно упругого центрально-сжатого стержня scr и действительным напряжением s следующего вида:
 . (36)
. (36)
В формуле (36) предел пропорциональности принят равным 0,85 sy, а отношение s / sу = 1 при scr/sy = 2,42, что эквивалентно отношению sy / scr = Еr/Е = 0,412 (где Еr - приведенный модуль).
Для балок двутаврового сечения с двумя осями симметрии критические напряжения примерно пропорциональны значению 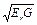 , где G = const. На этом основании принято scr/sy =
, где G = const. На этом основании принято scr/sy = 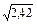 » 1,55 при s / sу = 1. В интервале 0,85 £ scr/sy £ 1,55 значение s / sу изменяется линейно, в связи с чем рекомендуется формула (см. п. 1* прил. 7* СНиП II-23-81*):
» 1,55 при s / sу = 1. В интервале 0,85 £ scr/sy £ 1,55 значение s / sу изменяется линейно, в связи с чем рекомендуется формула (см. п. 1* прил. 7* СНиП II-23-81*):
jb = 0,68 +0,21 j1 при j1 > 0,85. (37)
Балки двутаврового сечения с одной осью симметрии исследованы в [14]. При этом была принята та же методика, что и для сечений с двумя осями симметрии, но значения отношения Еr / Е принимались различными для верхнего и нижнего поясов балки. На основе этих исследований для практических расчетов рекомендуется табл. 81 СНиП II-23-81*.
5.23 (5.16*). Требование надежной связи сжатого пояса балки со сплошным жестким настилом, когда не нужна проверка устойчивости балок, должно быть предусмотрено в проектах строительных конструкций и производства работ.
При устройстве закреплений сжатого пояса в отдельных точках (узлы продольных или поперечных связей, точки крепления жесткого настила) такие закрепления следует рассчитывать на фактическую или условную поперечную силу в горизонтальной плоскости. При этом каждая точка закреплений предназначена для уменьшения расчетной длины сжатого пояса балки (см. п. 5.19 настоящего Пособия).
При непрерывном прикреплении сжатого пояса балки к жесткому настилу это прикрепление следует рассчитывать на максимальное значение эквивалентной поперечной нагрузки, действующей на пояс в горизонтальной плоскости [13]:
 , (38)
, (38)
где N - продольная сжимающая сила;
vb - начальное искривление пояса;
vu - искривление пояса при действии сжимающей силы N;
l - пролет балки.
С учетом формул (32) и (38) получим
 . (39)
. (39)
При плоском и профилированном металлических настилах или волнистой стали надежной связью является соединение их со сжатым поясом балки сваркой на болтах или дюбелях.
Сплошной просечно-вытяжной настил следует приваривать к сжатому поясу балки в соответствии с требованием ГОСТ 8706-78* о защемлении настила. При этом листы настила необходимо располагать просечкой поперек пролета (перпендикулярно оси балки).
Для сборных железобетонных плит из различных бетонов под надежной связью следует понимать крепление закладных деталей плит к сжатому поясу балки сваркой или на болтах.
При монолитных железобетонных плитах надежной связью может служить приварка арматуры или специальных закладных деталей к сжатому поясу балки либо замоноличивание этого пояса в слое бетона толщиной не менее 20 мм.
При устройстве прикреплений необходимо учитывать конструктивные требования для применяемого вида соединений (минимальные размеры швов, расстояния между болтами и от края элемента и т. д.).
5.24 (5.16*). Наибольшие значения условной гибкости верхнего пояса балки  , при которых не требуется выполнять расчет на устойчивость балок, определяются по формулам табл. 8* СНиП II-23-81*, которые получены на основе методики, изложенной в п. 5.22 настоящего Пособия, при выполнении условия jb = 1. Значения
, при которых не требуется выполнять расчет на устойчивость балок, определяются по формулам табл. 8* СНиП II-23-81*, которые получены на основе методики, изложенной в п. 5.22 настоящего Пособия, при выполнении условия jb = 1. Значения 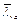 для различных значений b/t и h/b приведены в табл. 16.
для различных значений b/t и h/b приведены в табл. 16.
Таблица 16
| Место приложения нагрузки | b/t | Наибольшие значения 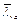 при значениях h/b, равны при значениях h/b, равны
| |||||
| К верхнему | 0,858 | 0,628 | 0,551 | 0,513 | 0,490 | 0,475 | |
| поясу | 0,774 | 0,594 | 0,534 | 0,504 | 0,486 | 0,474 | |
| 0,690 | 0,560 | 0,517 | 0,495- | 0,482 | 0,473 | ||
| 0,606 | 0,526 | 0,499 | 0,486 | 0,478 | 0,473 | ||
| 0,522 | 0,492 | 0,482 | 0,477 | 0,474 | 0,472 | ||
| К нижнему | 1,238 | 0,928 | 0,825 | 0,773 | 0,742 | 0,721 | |
| поясу | 1,154 | 0,894 | 0,807 | 0,764 | 0,738 | 0,720 | |
| 1,070 | 0,860 | 0,790 | 0,755 | 0,734 | 0,720 | ||
| 0,986 | 0,826 | 0,773 | 0,746 | 0,730 | 0,719 | ||
| 0,902 | 0,792 | 0,755 | 0,737 | 0,726 | 0,718 | ||
| Независимо от | 0,948 | 0,703 | 0,621 | 0,580 | 0,556 | 0,540 | |
| уровня приложения | 0,884 | 0,679 | 0,611 | 0,576 | 0,556 | 0,542 | |
| нагрузки при | 0,820 | 0,655 | 0,600 | 0,572 | 0,556 | 0,545 | |
| расчете участка | 0,756 | 0,631 | 0,589 | 0,568 | 0,556 | 0,547 | |
| между связями или при чистом изгибе | 0,692 | 0,607 | 0,579 | 0,564 | 0,556 | 0,550 |
Для получения значений lef / b значения 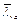 , приведенные в таблице, следует умножить на
, приведенные в таблице, следует умножить на 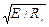 .
.
5.25 (5.17, 5.18). При изгибе балки в двух главных плоскостях потеря устойчивости выражается достижением предельной нагрузки (максимума на кривой состояний равновесия). В этом случае изгиб в обеих плоскостях и кручение возникают с самого начала нагружения и, постепенно возрастая, приводят к развитию пластических деформаций и исчерпанию несущей способности.
Для двутавровых балок, рассчитываемых по формуле (38) СНиП II-23-81*, проверку устойчивости при двухосном изгибе можно выполнять согласно рекомендациям ЕКМК [15], полученным как частный случай из уравнения взаимодействия для стержня, сжатого с двухосным эксцентриситетом, по формуле
 . (40)
. (40)
При приложении нагрузки, действующей в плоскости, параллельной плоскости х-х, только к одному (верхнему) поясу балки во втором члене формулы (40) следует принимать изгибающий момент My,f и момент сопротивления Wy,f соответственно для этого (верхнего) пояса балки. В этом случае расчет следует выполнять по формуле
 . (41)
. (41)
5.26 (5.18). Расчет статически определимых изгибаемых элементов, несущих статическую нагрузку, может выполняться по ограниченным пластическим деформациям в соответствии с предложением, выдвинутым Н. С. Стрелецким. В СНиП II-23-81* это предложение реализовано в виде коэффициентов сi > 1, вводимых к упругим моментам сопротивления сечений. При определении коэффициентов сi, (табл. 66 СНиП II-23-81*) в качестве количественного критерия было принято достаточно большое ограничение пластических деформаций с  (где
(где  ; er - остаточная деформация в сечении после полной упругой разгрузки). В общем случае при таком подходе уменьшение предельных моментов по сравнению с моментами, соответствующими полным пластическим шарнирам, составляет не более 3-5 %, а для двутавровых сечений - 1 %.
; er - остаточная деформация в сечении после полной упругой разгрузки). В общем случае при таком подходе уменьшение предельных моментов по сравнению с моментами, соответствующими полным пластическим шарнирам, составляет не более 3-5 %, а для двутавровых сечений - 1 %.
При одновременном действии в сечении момента М и поперечной силы Q учитывается кривая взаимодействия их предельных значений [16], в связи с чем вводимое в расчет отношение c1/c для двутавровых сечений при 0,5 Rs < t £ 0,9 Rs, [формула (43) СНиП II-23-81*] не должно превышать значений, приведенных в табл. 17 и вычисленных по формулам (43) и (44) СНиП II-23-81*.
Таблица 17
| t/rs | £ 0,50 | 0,55 | 0,60 | 0,65 | 0,70 | 0,75 | 0,80 | 0,85 | 0,90 |
| с1/c | 1,00 | 0,987 | 0,97 | 0,950 | 0,925 | 0,892 | 0,848 | 0,787 | 0,695 |
При этом значение коэффициента с1 не должно быть меньше единицы; в противном случае расчет необходимо выполнять в пределах упругой работы стали по формулам (28) и (29) СНиП II-23-81*.
При наличии в балке протяженной зоны чистого изгиба, когда развитие пластических деформаций предполагается не в одном сечении, а на определенном участке ее длины, с целью ограничения общих перемещений значение предельного момента уменьшается и принимается равным полусумме предельных моментов при работе сечения в пределах и за пределом упругости.
Методика расчета балок с учетом ограниченных пластических деформаций открывает новые возможности для их дальнейшей оптимизации. Для этого в п. 5.18 СНиП II-23-81* указано, что допускается принимать меньшие значения коэффициентов сi, соответствующие меньшим значениям пластических деформаций. Это позволяет рассчитывать балки при различных значениях ограниченных деформаций, что практически важно для получения оптимальных сечений с учетом назначения элемента, условий эксплуатации, конструктивного решения, формы сечения и соотношений его размеров и т. д. При этом проверку прочности сечения, местной устойчивости пластинок этого сечения, общей устойчивости балки и ее жесткости следует выполнять в зависимости от значения принимаемой деформации, правильный выбор которой обеспечит минимум площади сечения. Таким образом, основной задачей расчета с учетом ограниченных деформаций является проектирование балок минимальной массы 1.
__________
Бельский Г. Е. Оптимизация изгибаемых элементов на основе деформационного критерия // Строит. механика и расчет сооружений. - 1986. - № 2.- С. 8-11.
5.27 (7.5). Методика расчета стенок балок на устойчивость с учетом пластических деформаций основана на результатах решения задачи об устойчивости пластинки при совместном действии нормальных и касательных напряжений. Проверка устойчивости стенки заключается в сравнении изгибающего момента М для расчетного отсека, вычисленного в соответствии с указаниями п. 7.2* СНиП II-23-81*, с критическим Мcr при известных касательных напряжениях [17]. В качестве критического принимается момент, соответствующий потере устойчивости стенки при определенном напряженно-деформированном состоянии и условии, что устойчивость поясных листов обеспечена. При этом предполагалось, что с увеличением пластических деформаций степень защемления стенки в поясах уменьшается. При значительном развитии пластических деформаций, соответствующих критической гибкости стенки 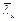 = 2,2, эффект защемления стенки в поясах не учитывается. Закрепление поперечных сторон расчетного отсека стенки принимается шарнирным независимо от степени развития пластических деформаций.
= 2,2, эффект защемления стенки в поясах не учитывается. Закрепление поперечных сторон расчетного отсека стенки принимается шарнирным независимо от степени развития пластических деформаций.
Расчет на устойчивость стенок балок двутаврового поперечного сечения с двумя осями симметрии, укрепленных только поперечными ребрами жесткости, следует выполнять по формуле (78) СНиП II-23-81*, которая устанавливает значение критического момента Мcr для всей балки. При этом в формуле (78) СНиП II-23-81* первое слагаемое выражает часть критического момента, воспринимаемого поясами балки Mf,cr = RyAfhefgc, а второе - часть критического момента, воспринимаемого стенкой Mw,cr = Ryh2eftagc. При отсутствии касательных напряжений (t = 0) максимальное значение Mw,cr = 0,24 Ryh2eftagc при 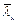 = 2,2.
= 2,2.
В табл. 18 приведены значения коэффициента a, вычисленные для различных значений 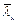 и t / Rs.
и t / Rs.
Для балок двухстенчатого сечения с двумя осями симметрии значение критического момента, получаемого по формуле (78) СНиП П-23-81*, необходимо умножать на коэффициент 2,0 и принять в этой формуле Аw = 2 heft.
5.28 (7.5). Стенки балок асимметричного сечения (с более развитым сжатым поясом), укрепленные только поперечными ребрами жесткости, работают в условиях совместного действия внецентренного растяжения и сдвига. Исследование работы таких стенок за пределом упругости [17] показали, что при проверке их устойчивости расчетную высоту можно принимать равной удвоенной высоте сжатой зоны, так как влияние остальной растянутой зоны стенки на ее устойчивость незначительно. Если в сжатой зоне стенки не возникает пластических деформаций [выполняются условия (28), (29), (31) СНиП II-23-81*], то ее устойчивость можно проверять по формуле (74) СНиП II-23-81*, принимая hef = 2 h1 (где h1 - высота сжатой зоны). Необходимо отметить, что появление пластических деформаций в растянутой зоне (s = M/Wmin > Ry) нарушает линейный закон распределения напряжений в сечении. С учетом этого фактора высоту сжатой зоны h1 и напряжения на кромке стенки следует определять из уравнений, соответствующих напряженно-деформированному состоянию в расчетном отсеке. Если напряжения в поясах балки асимметричного сечения равны Ry, то устойчивость ее стенки при ограничениях, указанных в п. 7.5 СНиП II-23-81*, можно проверить по формуле
 , (42)
, (42)
где A1 и A2 - соответственно площади сжатого и растянутого поясов;
 - принимается по формуле
- принимается по формуле
 ; (43)
; (43)
a - коэффициент, определяемый по формуле (78) СНиП П-23-81* или принимаемый по табл. 18 настоящего Пособия.
Для балок двухстенчатого сечения значение критического момента, получаемое в правой части формулы (42), необходимо умножать на коэффициент 2,0 и принять в этой формуле Аw = 2 heft.
5.29 (7.24). Расчет на устойчивость поясных листов (полок) балок с учетом развития пластических деформаций рекомендуется выполнять в предположении их шарнирного опирания по линии соединения поясов со стенкой при условии, что длина полуволны пластинки равна 3 bef (где bef - расчетная ширина свеса). Наибольшие значения отношения bef / t, приведенные в табл. 30 СНиП П-23-81*, получены из условия равноустойчивости стенки и сжатого пояса балки при чистом изгибе, так как в этом случае деформации сжатого пояса достигают максимальных значений.
При действии касательных напряжений в расчетном отсеке балки отношения bef / t могут быть увеличены и приняты по табл. 19 настоящего Пособия, в которой учитывается уменьшение деформаций в поясе за счет касательных напряжений в стенке.
Минимальные значения условной гибкости для свесов при чистом изгибе  соответствуют значительному развитию пластических деформаций; максимальные -
соответствуют значительному развитию пластических деформаций; максимальные -  с некоторым запасом соответствуют такому уровню нагрузки, при котором в поясах балки сжимающие напряжения достигают значения Ry.
с некоторым запасом соответствуют такому уровню нагрузки, при котором в поясах балки сжимающие напряжения достигают значения Ry.
Таблица 18
| t/Rs | Значения a при  , равной , равной
| |||||||||||
| 2,2 | 2,5 | 2,7 | 3,0 | 3,2 | 3,5 | 3,7 | 4,0 | 4,2 | 4,5 | 4,7 | 5,0 | |
| 0,0 | 0,240 | 0,239 | 0,237 | 0,234 | 0,231 | 0,225 | 0,221 | 0,213 | 0,206 | 0,195 | 0,187 | 0,174 |
| 0,1 | 0,239 | 0,238 | 0,237 | 0,234 | 0,231 | 0,225 | 0,220 | 0,212 | 0,205 | 0,194 | 0,186 | 0,173 |
| 0,2 | 0,234 | 0,233 | 0,232 | 0.229 | 0,226 | 0,220 | 0,215 | 0,206 | 0,200 | 0,189 | 0,181 | 0,167 |
| 0,3 | 0,227 | 0,226 | 0,225 | 0,222 | 0,219 | 0,213 | 0,208 | 0,199 | 0,193 | 0,182 | 0,174 | 0,160 |
| 0,4 | 0,216 | 0,215 | 0,214 | 0,211 | 0,208 | 0,202 | 0,197 | 0,188 | 0,182 | 0,171 | 0,163 | 0,149 |
| 0,5 | 0,203 | 0,202 | 0,200 | 0,198 | 0,195 | 0,189 | 0,184 | 0,175 | 0,169 | 0,158 | 0,150 | 0,136 |
| 0,6 | 0,186 | 0,185 | 0,184 | 0,181 | 0,178 | 0,172 | 0,167 | 0,158 | 0,152 | 0,141 | 0,133 | 0,119 |
| 0,7 | 0,167 | 0,166 | 0,165 | 0,162 | 0,159 | 0,153 | 0,148 | 0,140 | 0,133 | 0,122 | 0,114 | 0,100 |
| 0,8 | 0,144 | 0,136 | 0,142 | 0,139 | 0,136 | 0,130 | 0,125 | 0,116 | 0,110 | 0,099 | 0,091 | 0,077 |
| 0,9 | 0,119 | 0,118 | 0,117 | 0,114 | 0,111 | 0,105 | 0,100 | 0,091 | 0,085 | 0,074 | 0,066 | 0,052 |
Таблица 19
| Сече- | tIRs | Значения 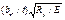 при при  , равной , равной
| ||||||
| ние | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | |
| 0,0 | 0,30 | 0,30 | 0,33 | 0,38 | 0,44 | 0,50 | 0,55 | |
| 0,1 | 0,30 | 0,30 | 0,33 | 0,40 | 0,45 | 0,52 | 0,57 | |
| 0,2 | 0,30 | 0,30 | 0,33 | 0,41 | 0,46 | 0,52 | 0,59 | |
| 0,3 | 0,30 | 0,30 | 0,34 | 0,42 | 0,47 | 0,53 | 0,60 | |
| 0,4 | 0,30 | 0,30 | 0,34 | 0,43 | 0,48 | 0,55 | 0,60 | |
| Двутав- | 0,5 | 0,30 | 0,31 | 0,36 | 0,44 | 0,50 | 0,57 | 0,60 |
| ровое | 0,6 | 0,30 | 0,32 | 0,38 | 0,46 | 0,52 | 0,60 | 0,60 |
| 0,7 | 0,30 | 0,34 | 0,40 | 0,50 | 0,56 | 0,60 | 0,60 | |
| 0,8 | 0,30 | 0,36 | 0,44 | 0,55 | 0,58 | 0,60 | 0,60 | |
| 0,9 | 0,32 | 0,40 | 0,52 | 0,60 | 0,60 | 0,60 | 0,60 | |
| 0,0 | 0,75 | 0,92 | 1,10 | 1,25 | 1,40 | 1,55 | 1,70 | |
| 0,1 | 0,75 | 0,92 | 1,10 | 1,26 | 1,42 | 1,58 | 1,72 | |
| 0,2 | 0,75 | 0,93 | 1,11 | 1,28 | 1,44 | 1,61 | 1,75 | |
| 0,3 | 0,76 | 0,95 | 1,13 | 1,30 | 1,47 | 1,65 | 1,80 | |
| Короб- | 0,4 | 0,77 | 0,97 | 1,15 | 1,33 | 1,50 | 1,69 | 1,85 |
| чатое | 0,5 | 0,78 | 1,00 | 1,18 | 1,37 | 1,55 | 1,75 | 1,95 |
| 0,6 | 0,80 | 1,03 | 1,21 | 1,42 | 1,62 | 1,82 | 2,05 | |
| 0,7 | 0,85 | 1,10 | 1,28 | 1,50 | 1,70 | 1,95 | 2,10 | |
| 0,8 | 0,90 | 1,20 | 1,40 | 1,65 | 1,90 | 2,15 | 2,20 | |
| 0,9 | 1,00 | 1,30 | 1,60 | 1,90 | 2,20 | 2,30 | 2,30 |
5.30 (5.20). Для балок, изгибаемых в плоскости наибольшей жесткости и рассчитываемых с учетом развития пластических деформаций, необходимо обеспечить их общую устойчивость из плоскости изгиба. При этом более высокий уровень развития пластических деформаций в балках (что связано с увеличением коэффициентов сi), требует более частой развязки сжатого пояса в горизонтальной плоскости вплоть до непрерывного его закрепления жестким настилом. При максимальных значениях коэффициентов сi равных значениям с по табл. 66 СНиП II-23-81*, следует уменьшать значения отношений lef/b по табл. 16 умножением на коэффициент d = 0,3 или применять непрерывное закрепление пояса; при сi = 1,0, что соответствует работе балки в пределах упругости, значения отношений lef/b следует принимать по табл. 16. Для промежуточных случаев в СНиП II-23-81* допускается линейная интерполяция.
Указанные в п. 5.20 СНиП II-23-81* требования относятся к случаю чистого изгиба и соответствуют принятому значению ограничения пластических деформаций в сечении.
При действии, например, сосредоточенной силы в середине балки значения отношений lef/b могут быть увеличены на 25 % по сравнению с их значениями при чистом изгибе.
5.31 (5.22). При условиях, указанных в п. 5.22 СНиП II-23-81*, расчет неразрезных и защемленных балок может выполняться с одновременным учетом работы сечений за пределом упругости и соответствующего перераспределения опорных и пролетных изгибающих моментов. Практическая методика расчета сводится к определению коэффициента перераспределения моментов а, вводимого к наибольшему изгибающему моменту в пролете или на опоре 1.
_________
Чернов Н. П. Расчет стальных неразрезных балок по ограниченным пластическим деформациям // Строит. механика и расчет сооружений. - 1980. - № 2. - С. 68-71.
Формула (46) СНиП II-23-81* для определения коэффициента а получена из условия ограничения максимальных остаточных деформаций в сечении значением 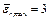 (где
(где  = er,тах Е/Rу).
= er,тах Е/Rу).
В соответствии с требованиями п. 5.22 СНиП II-23-81* допускается принимать значения коэффициента a, соответствующие меньшему ограничению пластических деформаций  < 3. В этом случае коэффициент a необходимо определять по формуле
< 3. В этом случае коэффициент a необходимо определять по формуле
 . (44)
. (44)
Проверку прочности в характерных сечениях неразрезных балок необходимо выполнять согласно требованиям п. 5.22 СНиП II-23-81* с учетом одновременного действия в сечении изгибающего момента M и поперечной силы Q.
5.32 (5.23). При изгибе неразрезных балок в двух главных плоскостях коэффициенты перераспределения изгибающих моментов a необходимо определять в каждой плоскости отдельно с учетом условий и требований, относящихся к балкам, изгибаемым в одной плоскости.
5.33 (5.22). Рассмотрим примеры расчета неразрезных балок за пределом упругости.
Пример 1. Определить значение коэффициента a для четырехпролетной балки, нагруженной сосредоточенными силами в третях каждого пролета (рис. 7, а).
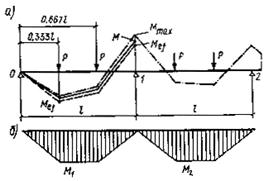
Рис. 7. Перераспределение изгибающих моментов в неразрезной балке
а - схема нагружения и эпюры моментов; б - эпюры моментов для свободно опертых балок
Наибольший изгибающий момент, определяемый из расчета неразрезной балки в предположении упругой работы материала, действует на опоре 1 и его значение равно Мmах 0,2856 Рl.
Найдем наибольшее значение изгибающего момента Mef. Изгибающий момент в крайнем пролете, вычисляемый как в свободно опертой балке (рис. 7, б), при а = 0,3333 l равен M1 = 0,3333 Pl.
По формуле (47) СНиП II-23-81* находим
 .
.
Для второй силы в этом пролете при а = 0,6667 l получим
 .
.
Для промежуточного пролета имеем M2 = 0,3333 Pl; по формуле (48) СНиП II-23-81* находим
Мef = 0,5 M2 = 0,3333 Pl /2 = 0,1667 Pl.
Наибольшее значение Mef = 0,25 Рl. По формуле (46) СНиП II-23-81* находим a - значение коэффициента перераспределения моментов

Расчетное значение изгибающего момента М равно
М = aМmах = 0,9376 × 0,2856 Pl = 0,2678 Pl.
Уменьшение изгибающего момента за счет перераспределения моментов составляет 6,24 %. Эпюра расчетных моментов показана на рис. 7, а сплошной линией.
Пример 2. Определить значение коэффициента a для однопролетной статически неопределимой балки (рис. 8).

Рис. 8. Эпюры моментов в однопролетной статически неопределимой балке
Пластические деформации ограничены значением  .
.
Наибольший изгибающий момент в заданной балке при упругой работе материала действует в заделке и его значение равно Мтах = 0,125 ql2. Наибольший изгибающий момент в пролете на расстоянии а = 0,375 l от левой опоры равен М = 0,07031 ql2. Изгибающий момент M1 на расстоянии а = 0,375 l от левой опоры, вычисленный как в однопролетной свободно опертой балке, равен M1 = 0,1172 ql2.
По формуле (47) СНиП II-23-81* находим
 .
.
Значение коэффициента a определяем по формуле (44)
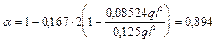 .
.
Расчетное значение изгибающего момента М равно
М = 0,894 × 0,125 ql2 = 0,112 ql2.
Уменьшение расчетного момента за счет перераспределения моментов составляет 10,6 %. Эпюра расчетных моментов М показана на рис. 8 сплошной линией.
Пример 3. Определить значение коэффициента a для однопролетной балки с обоими защемленными концами (рис. 9).

Рис. 9. Эпюры моментов в однопролетной балке с обоими защемленными концами
Наибольший изгибающий момент в заданной балке при упругой работе материала достигается одновременно на опорах и в пролете; его значение равно Мтах = 0,125 Pl. Изгибающий момент в середине пролета, вычисленный как в однопролетной свободно опертой балке, равен М 3 = 0,25 Pl. Согласно п. 5.22 б СНиП II-23-81 * имеем a = 1.
В рассматриваемой балке перераспределения изгибающих моментов при работе материала за пределом упругости не происходит.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 659; Нарушение авторских прав?; Мы поможем в написании вашей работы!